Konkav vs. konvex?

Was ist der Unterschied zwischen konkav und konvex?

Wenn wir den Unterschied zwischen konkav und konvex so allgemein wie möglich beschreiben würden, würden wir sagen, dass jedes hohle, schüsselartige Objekt konkav ist, während jedes Objekt, das einem Rugbyball oder Fußball ähnelt, eine konvexe Form hat. Aber vielleicht werden konvex und konkav deshalb so häufig falsch verwendet, weil die beiden Wörter nicht so einfach sind, wie wir sie gerne hätten.

Die meisten grammatikalischen Quellen bestehen darauf, dass die Verwendung von Mnemotechniken möglich ist, um konvex und konkav durch das Wort Höhle zu entschlüsseln. Während die Vorstellung, konkav mit dem Ereignis zu assoziieren, dass etwas „einfällt“, dabei hilft, etwas über Oberflächenmerkmale zu lernen, ist es verwirrend, diese Idee auf Themen zu beziehen, die mit Graphen zu tun haben.

Um zu verstehen, wie sich konkav und konvex voneinander unterscheiden, müssen wir lernen, wie jeder Begriff in der Mathematik, bei Spiegeln, Linsen und schließlich beim kreativen Schreiben verwendet wird. Sobald Sie sich entschieden haben, in welchem Zusammenhang Sie Wörter wie konkav und konvex verwenden möchten, können Sie sie mit mehr Selbstvertrauen in der Alltagssprache verwenden, wenn Sie ihre technischen Aspekte kennen.

Was bedeutet konkav?

Konkav wird als Adjektiv oder Substantiv verwendet, um die Form eines Objekts oder einer Oberfläche zu beschreiben, die nach innen gewölbt oder wie eine Schale ausgehöhlt ist. Beispiele für konkav in einem Satz sind:

„Sie schöpfte das Eis aus dem Behälter und hinterließ einen konkaven Fußabdruck.“

Nach dem Oxford Dictionary of Word Histories stammt das Wort konkav aus dem Spätmittelenglischen. Konkav und Konkavität geben den lateinischen Begriff concavus (con- und cavus) wieder, der mit ‚zusammen‘ und ‚hohl‘ übersetzt werden kann („Concave“, 110).

Synonyme von konkav sind:

Eingedrückt, niedergedrückt, gewölbt, hohl, eingedrückt, vertieft und versenkt.

Antonyme von konkav sind:

Ausbauchend, gewölbt, vorstehend, ausladend, vorspringend.

Was bedeutet konvex?

Das Wort konvex oder Konvexität ist ein Adjektiv, das einen Gegenstand oder eine Oberfläche beschreibt, die abgerundet oder gewölbt ist. In Bezug auf Objekte ist die mittlere Fläche eines konvexen Objekts breiter als seine äußere Ecke. Beispiele für konvex in einem Satz sind:

„Ich bin in Giftefeu gefallen und habe jetzt rote, konvexe Beulen auf meiner ganzen Haut.“

Synonyme von konvex sind:

Gewölbt, gebogen, wulstig, erhaben.

Antonyme von konvex sind:

Gedrückt, sinkend.

Konkave vs. konvexe Funktionen

Eine konvexe Funktion stellt eine kontinuierliche Linie auf einem Graphen dar, bei der der Mittelpunkt oder der Medianwert eines Bereichs den Mittelwert des Intervalls nicht überschreitet. Eine konkave Funktion ist das genaue Gegenteil einer konvexen Funktion, denn damit f(x) konkav ist, muss f(x) negativ sein. Um die Unterschiede deutlicher zu machen, hier ein kurzer Überblick über den Vergleich der Begriffe:

Konkav nach oben = konvex = konvex nach unten

Konkav nach unten = konkav = konvex nach oben

Der Unterschied zwischen konkaven und konvexen Funktionen wird deutlicher, wenn man sich ein Diagramm ansieht. Beachte, wie sich die konvexe Funktion nach oben öffnet, während sich die konkave Funktion nach unten öffnet.

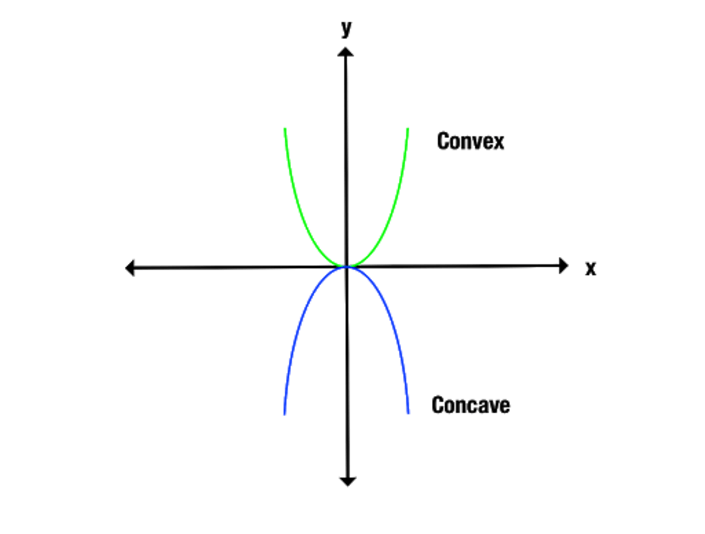
Eine weitere Möglichkeit, konkave und konvexe Funktionen zu erkennen, ist die Verbindung von Punkten auf dem Graphen entlang der x-Achse. Eine konkave Funktion verbindet nur Linien unterhalb des Graphen, während eine konvexe Funktion nur Linien oberhalb des Graphen erzeugt.

Wir können zusätzlich die Infinitesimalrechnung verwenden, um herauszufinden, ob eine Funktion konvex oder konkav ist oder nicht. Wenn die zweite Ableitung von f(x) größer als Null ist, dann ist die Funktion konvex. Ist aber die zweite Ableitung von f(x) kleiner als Null, so ist die Funktion konkav.

Konvexe vs. konkave Polygone

Nicht erschrecken, aber die Begriffe konvex und konkav werden auch in der Geometrie verwendet. Konvexe und konkave Formen werden am häufigsten in Bezug auf Polygone diskutiert, die Formen mit mindestens drei Seiten und Winkeln sind.

Es gibt regelmäßige Polygone mit gleichen Seiten und Winkeln, aber konvexe und konkave Polygone sind etwas komplizierter. Konvexe Polygone enthalten Innenwinkel, die kleiner als 180 Grad sind, während konkave Polygone einen oder mehrere Innenwinkel enthalten, die größer als 180 Grad sind.

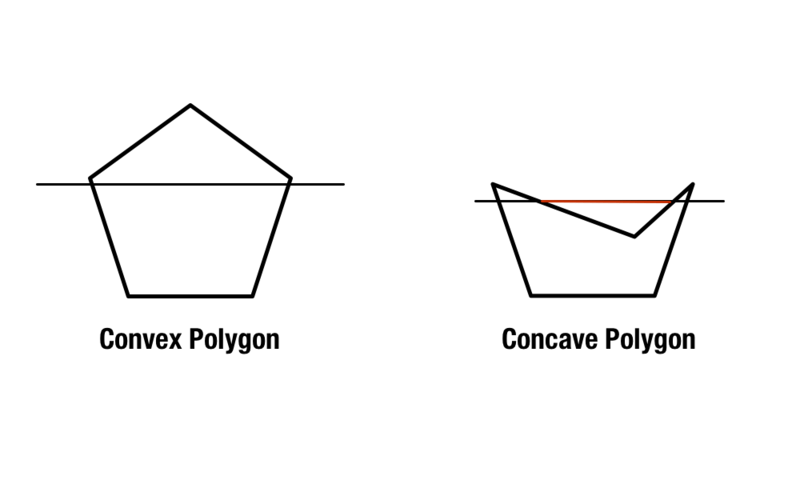
Eine zweite Methode, um konkave und konvexe Polygone zu identifizieren, besteht darin, zwei diagonale Linien durch die Form zu ziehen, ausgehend von den Ecken der Form. Wenn jede Linie innerhalb der Form verläuft, ist die Form konvex. Wenn sich mindestens eine Linie außerhalb der Form kreuzt, ist sie konkav.

Konkave vs. konvexe Spiegel

Die Begriffe konkav und konvex werden häufig verwendet, wenn es um optische Objekte wie Spiegel und Linsen geht. Jede konvexe Oberfläche ragt nach außen, ähnlich wie eine Blase, was den Effekt der Weite erzeugt. Konvexe Spiegel sind häufig in Parkhäusern zu finden, wo Autofahrer einen weiten Blick um Ecken oder mögliche tote Winkel benötigen.

Im Gegensatz dazu ist ein konkaver Spiegel nach innen gewölbt und erzeugt eine vergrößerte Reflexion, die auf dem Kopf steht. Wie die University of South Wales‘ School of Physics gezeigt hat, kann jeder, der einen glänzenden Löffel besitzt, diese Beobachtung testen, indem er sein Spiegelbild im Löffel betrachtet. Auf der konkaven Oberfläche des Löffels, wo man sein Essen aufnimmt, wird das Spiegelbild eng verzerrt, und man steht auf dem Kopf. Wenn du den Löffel aber auf die konvexe Seite drehst, ist dein Spiegelbild aufrecht und kleiner.

Die Spiegelungen unterscheiden sich so stark zwischen konvexen und konkaven Oberflächen, weil der Spiegel selbst Teil einer Kugel ist, unabhängig davon, ob die Oberfläche nach außen oder nach innen gewölbt ist. Da die Oberfläche einer Kugel nicht flach ist, legt das von der Oberfläche reflektierte Licht unterschiedliche Strecken zurück, bevor es den Spiegel berührt.

Abhängig davon, mit welchem Bereich der Oberfläche das Licht in Berührung kommt, kann ein Lichtstrahl von nahegelegenen Oberflächen reflektiert werden, um einen stärker gebündelten Bereich der Sichtbarkeit zu erzeugen. Deshalb sieht man bei der Betrachtung der Innenseite eines Löffels vielleicht nur die Reflexion dessen, was der Oberfläche des Löffels am nächsten ist – auch wenn er noch kleiner erscheint. Außerdem kann die Oberfläche des Spiegels, wenn man den Finger in den Löffel steckt, zwei oder drei verschiedene Reflexionen gleichzeitig erzeugen.

Konkave Linse vs. konvexe Linse

Konkave und konvexe Linsen gibt es in Alltagsgegenständen wie Brillen, Kontaktlinsen, Ferngläsern und Teleskopen. Ähnlich der Wissenschaft, die hinter der Lichtreflexion an konvexen und konkaven Spiegeln steht, gibt es auch Muster dafür, wie Licht durch konkave und konvexe Linsen hindurchgeht, um ein sichtbares Bild zu erzeugen.

Konvexe Linsen

Nach der Manocha-Akademie werden konvexe Linsen Konvergenzlinsen genannt, weil sie in der Lage sind, Bilder zu erzeugen, die verkleinert, vergrößert oder introvertiert sind. Wie genau ein Bild durch eine Konvexlinse erscheint, hängt davon ab, wie nah das Objekt am Brennpunkt der Linse ist. Bei jeder Konvexlinse gibt es symmetrische Brennpunkte auf beiden Seiten der Linse.

Wie genau ein Objekt durch eine konvexe Linse abgebildet wird, lässt sich anhand von drei Prinzipien vorhersagen:

Prinzip 1: Jeder Lichtstrahl, der durch eine konvexe Linse fällt, verläuft parallel zur Hauptachse, die eine zentrale Linie ist, die durch den absoluten Mittelpunkt einer sphärischen Linse verläuft. Sobald das Licht die Linse berührt, wird es gebrochen und tritt auf der anderen Seite in den Brennpunkt ein. Vorübergehende Lichtstrahlen, die parallel zur Hauptachse verlaufen, bewegen sich über dem Objekt vor der Linse.

Prinzip 2: Jeder Lichtstrahl, der durch den Mittelpunkt einer konvexen Linse verläuft, setzt sich auf der anderen Seite in einer geraden Linie fort.
Prinzip 3: Jeder Lichtstrahl, der durch einen Brennpunkt auf der gleichen Seite wie das Objekt verläuft, wird beim Kontakt mit der Linse gebrochen und verläuft auf der anderen Seite parallel zur Hauptachse.

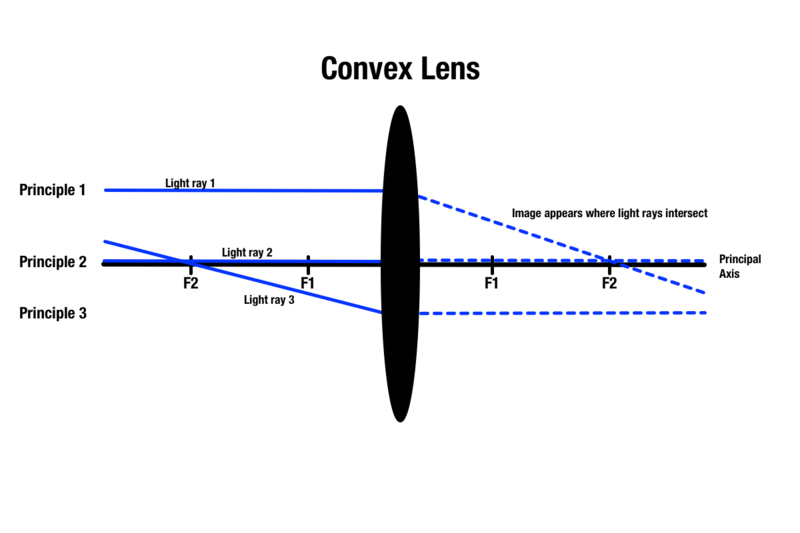
Während es drei Prinzipien für die Vorhersage der Bildqualität durch eine Konvexlinse gibt, können beim Zeichnen eines Strahlendiagramms nur zwei Prinzipien auf ein Objekt angewendet werden. Zwei beliebige Prinzipien ergeben einen Schnittpunkt des Lichts auf der anderen Seite der Linse, der den Bereich angibt, in dem das Bild des Objekts erscheint.

Je weiter ein Objekt von einer Konvexlinse entfernt ist, desto kleiner wird das Bild auf der anderen Seite sein, und je näher ein Objekt an der Konvexlinse ist, desto größer wird es erscheinen. Ein Objekt, das sich hinter dem nächstgelegenen Brennpunkt befindet, erzeugt ein größeres Bild hinter dem Objekt. Wie die Manocha Academy hervorhebt, wird diese Art der Linsenvergrößerung für optische Hilfsmittel wie Lupen verwendet.

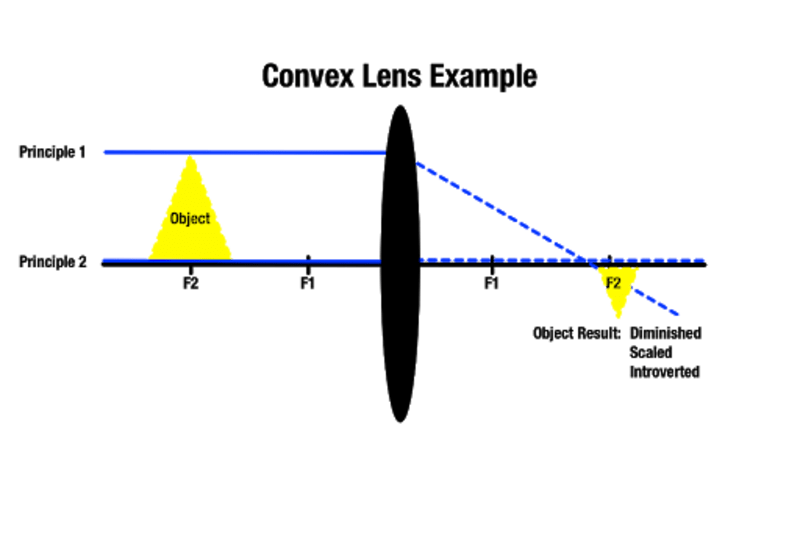
Abhängig davon, in welchem Brennpunkt sich ein Objekt befindet, ist es möglich, ein Bild zu erzeugen, das in etwa die gleiche Größe hat. Es ist auch möglich, echte Bilder zu erzeugen, die nicht sichtbar sind, wenn sich die vorbeilaufenden Lichtstrahlen nie schneiden, weil sie auf der anderen Seite parallel sind. In diesem Fall existiert das erzeugte Bild in einer unendlichen Entfernung.

Konkave Linsen

Jede konkave Linse hat einen dickeren Durchmesser und eine dünnere Mitte, da eine konkave Linse nach innen gebogen ist. Die Form konkaver Linsen erlaubt es dem Licht, sich auszubreiten, sobald es mit der Linse in Berührung kommt, wodurch virtuelle Objekte kleiner erscheinen. Die Fähigkeit der konkaven Linse, das Licht zu verteilen, macht sie zu einer idealen Linse für Werkzeuge wie Taschenlampen, bei denen eine zentrale Lichtquelle über eine größere Fläche genutzt werden kann.

Konkavlinsen erzeugen Bilder mit drei Prinzipien, die denen von Konvexlinsen ähnlich sind:

Prinzip 1: Jeder Lichtstrahl, der oberhalb des Objekts und parallel zur Hauptachse verläuft, wird beim Auftreffen auf die Linse gebrochen und erscheint so, als käme er aus der Richtung des nächstgelegenen Brennpunkts.

Grundsatz 2: Jeder Lichtstrahl, der durch den Mittelpunkt der konkaven Linse geht, wird ohne Brechung durchgelassen.
Prinzip 3: Jeder Lichtstrahl, der auf einen Brennpunkt auf der anderen Seite der konkaven Linse gerichtet ist, wird gebrochen und parallel zur Hauptachse verlaufen.

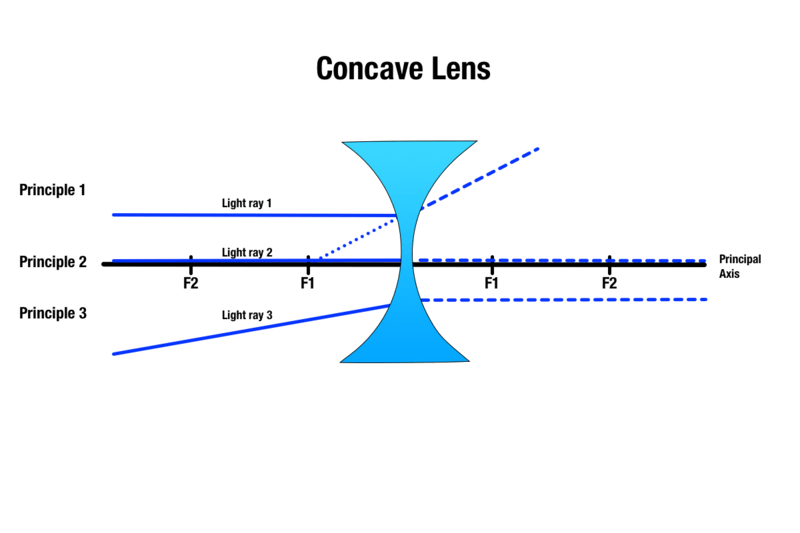
Während die Größe des Objektbildes je nach Entfernung des Objekts von einer konkaven Linse variiert, ist das erzeugte Bild immer virtuell, aufrecht, kleiner und erscheint auf derselben Seite der Linse wie das Objekt.

Konkav vs. konvex in der Schrift

Die Wörter konkav und konvex sind einander entgegengesetzt und beschreiben im Wesentlichen die Form von Objekten oder Oberflächen in der gleichen Weise, wie wir Wörter gegenüberstellen wie:

• Klein vs. groß
• groß vs. kurz
• schlank vs. breit
• rund vs. flach

Da konkav und konvex technische Wörter sind, kann ihre Verwendung in der Prosa zu einer eher metaphorischen oder abstrakten Interpretation für ein flüchtiges Publikum führen. Das bedeutet, dass ein Autor, der sich entschließt, konkav oder konvex außerhalb ihres typischen Verwendungsbereichs zu verwenden, entscheiden muss, wie klar er sein Schreiben gestalten will.

Betrachten Sie das Adjektiv

Ein prominentes Beispiel für die Verwendung von konkav oder konvex in der Literatur sind die Schriften des amerikanischen Autors David Foster Wallace (oder kurz DFW). DFW ist berüchtigt für seinen komplexen und technischen Schreibstil – und ja, er hat mehrmals konvex und konkav verwendet, um Substantive zu beschreiben. Wallace verwendet konkav und konvex in den folgenden Beispielen:

„Mein Hand-Auge war in Ordnung, aber ich war weder groß noch schnell, hatte eine fast konkave Brust und Handgelenke, die so dünn waren, dass ich sie mit Daumen und kleinem Finger zusammenhalten konnte…“

– „Tennis, Trigonometrie, Tornados: A Midwestern Boyhood“, Harper’s Magazine.

„…Puppenaugen, die sich mit dem Zug einer Herzschnur öffnen, konkav, wo ich konvex bin.“

– „Order and Flux in Northampton“, Conjunctions.

Die Verwendung von DFW-Beispielen soll nicht nur zeigen, wie Autoren konvex oder konkav außerhalb des mathematischen Kontextes verwendet haben, sondern die Autoren sollen vielmehr darüber nachdenken, ob die Verwendung von technischen oder abstrakten Begriffen für eine klare Kommunikation mit ihrem Publikum hilfreich ist.
Im ersten DFW-Beispiel ist die Verwendung von konkav sinnvoll, weil er die Struktur von etwas beschreibt. Die Verwendung von konkav und konvex zur Beschreibung von nicht-objektiven Substantiven, wie z. B. Gefühle oder Gedanken, führt jedoch dazu, dass die Bedeutung dessen, was wir zu erklären versuchen, verschleiert wird. Das zweite DFW-Beispiel bewegt sich bei der Verwendung von konvex und konkav auf einem schmalen Grat, weil ihre Verwendung sowohl wörtlich als auch metaphorisch ist.

FAQ: Verwandte Begriffe

Was ist eine Funktion?

Eine Funktion ist die Gleichung einer Linie in einem Diagramm. Funktionen sind für jede Linie in einem Graphen anders, aber sie haben die allgemeine Form,

f(x) = x + 1

Bei jeder Linienfunktion ist die abhängige Variable normalerweise f(x), während jede unbekannte Variable innerhalb der Funktion als unabhängige Variable bezeichnet wird.

Was ist die Domäne?

Die Domäne ist eine Menge unabhängiger Variablen in einem Graphen, der der Funktion einer Linie entspricht. Domänen sind wichtig zu verstehen, weil sie bestimmte Punkte auf dem Diagramm lokalisieren, die jedem realen Ausgang einer Gleichung entsprechen.

Was ist der Bereich?

Der Bereich einer Funktion stellt jeden möglichen Wert entlang der x- oder y-Achse in einem Diagramm dar, der einen gültigen Wert für die abhängige Variable ergibt. Alle Minimal- und Maximalwerte werden durch Ersetzen der Variablen auf der x- oder y-Achse ermittelt.

Was ist ein Intervall?

Ein Intervall ist eine Menge von Zahlen, die die ganzen Zahlen einer Linie, auch Domäne genannt, darstellen. Ein geschlossenes Intervall umfasst zwei endliche Punkte einer Linie, wobei die Linie außerhalb des Bereichs einer ganzen Zahl nicht mehr existiert. Ein offenes Intervall ist eine Menge von ganzen Zahlen, die nicht das absolute Ende des Bereichs einer Linie darstellen.

Teste dich selbst!

Teste mit den folgenden Multiple-Choice-Fragen, wie gut du den Unterschied zwischen konvex und konkav verstehst:

1. Während du einen glänzenden Löffel betrachtest, bemerkst du, dass dein Spiegelbild auf dem Kopf steht. Die Oberfläche des Löffels ist eine _________ Oberfläche.
   a. Konvex
   b. Spiegel
   c. Konkav
   d. Metall
2. Eine konvexe Funktion wird im Zusammenhang mit der graphischen Darstellung von Funktionen manchmal als:
   a. Konkav nach oben
   b. Konvex nach unten
   c. Konkav nach unten
   d. A und B
3. Welche der folgenden Aussagen beschreibt keine konkave Fläche:
   a. Hohle Halbkugel
   b. Augenlinse
   c. Müslischale
   d. Halbkugel
4. Welcher der folgenden Begriffe beschreibt keine konvexe Fläche:
   a. Die Figur Stewie aus Family Guy
   b. Sphäre
   c. Parkhausspiegel
   d. Fußball
5. Welche der folgenden Formen kann nicht als konkaves Polygon existieren:
   a. Fünfeck
   b. Sechseck
   c. Dreieck
   d. Achteck

Antworten

1. C: Konkav
2. D: A und B
3. D: Halbkugel
4. B: Kugel
5. C: Dreieck

Quellen:

1. Bourne, M. „Domain and Range of a Function.“ Interactive Mathematics, Jan. 4, 2019.
2. „Concave.“ Merriam-Webster Dictionary, 2019.
3. „Concave.“ The Oxford Dictionary of Word Histories, Ed. Chantrell, 2002, S. 110.
4. „Concave and Convex Mirrors.“ Manocha Academy, YouTube, 2019.
5. „Konkavlinse: Definition & Uses.“ Study.com, 2019.
6. „Convex.“ Merriam-Webster Dictionary, 2019.
7. „Konvexe und konkave Linsen.“ Manocha Academy, YouTube, 2019.
8. „Mathematics / Understanding Polygons.“ Learnhive Inc, 2018.
9. „Reflection from a concave mirror.“ UNSW Physics, YouTube, 2017.
10. Wallace, D.F. „Tennis, Trigonometry, Tornadoes: A Midwestern Boyhood.“ Harper’s Magazine, 1991.
11. Wallace, D.F. „Order and Flux in Northampton“. Conjunctions, 1991.
12. Weisstein, Eric W. „Concave Function.“ MathWorld-A Wolfram Web Resource, n.d.
13. Weisstein, Eric W. „Convex Function.“ MathWorld-A Wolfram Web Resource, n.d.

Der Wortzähler ist ein dynamisches Online-Tool zum Zählen von Wörtern, Zeichen, Sätzen, Absätzen und Seiten in Echtzeit, zusammen mit einer Rechtschreib- und Grammatikprüfung.