Introductory Business Statistics

Betrachten Sie den folgenden Datensatz.
4; 5; 6; 6; 6; 7; 7; 7; 7; 7; 7; 8; 8; 8; 9; 10

Dieser Datensatz kann durch das folgende Histogramm dargestellt werden. Jedes Intervall hat die Breite eins, und jeder Wert befindet sich in der Mitte eines Intervalls.

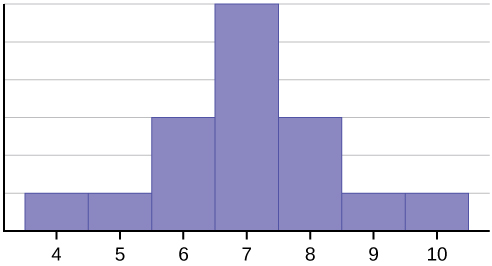
Das Histogramm zeigt eine symmetrische Verteilung der Daten. Eine Verteilung ist symmetrisch, wenn an einem Punkt des Histogramms eine vertikale Linie gezogen werden kann, so dass die Form links und rechts der vertikalen Linie spiegelbildlich zueinander ist. Der Mittelwert, der Median und der Modus sind jeweils sieben für diese Daten. Bei einer perfekt symmetrischen Verteilung sind der Mittelwert und der Median identisch. In diesem Beispiel gibt es nur einen Modus (unimodal), und der Modus ist derselbe wie der Mittelwert und der Median. Bei einer symmetrischen Verteilung mit zwei Modi (bimodal) würden sich die beiden Modi von Mittelwert und Median unterscheiden.

Das Histogramm für die Daten: 4566677778 ist nicht symmetrisch. Die rechte Seite scheint im Vergleich zur linken Seite „abgehackt“ zu sein. Eine solche Verteilung wird als schief nach links bezeichnet, weil sie nach links gezogen ist. Wir können die Schiefe einer Verteilung formell messen, genauso wie wir das Mittelgewicht der Daten oder ihre allgemeine „Speadness“ mathematisch messen können. Die mathematische Formel für die Schiefe lautet: . Je größer die Abweichung von Null ist, desto größer ist der Grad der Schiefe. Ist die Schiefe negativ, so ist die Verteilung linksschief (siehe Abbildung). Ein positives Maß für die Schiefe zeigt eine rechte Schiefe an, wie in (Abbildung).

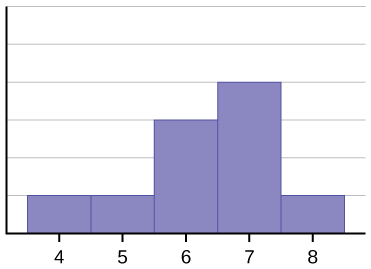
Der Mittelwert ist 6,3, der Median ist 6,5 und der Modus ist sieben. Beachten Sie, dass der Mittelwert kleiner ist als der Median und beide kleiner sind als der Modus. Sowohl der Mittelwert als auch der Median spiegeln die Schieflage wider, aber der Mittelwert spiegelt sie stärker wider.

Das Histogramm für die Daten: 67777888910, ist ebenfalls nicht symmetrisch. Es ist nach rechts geneigt.

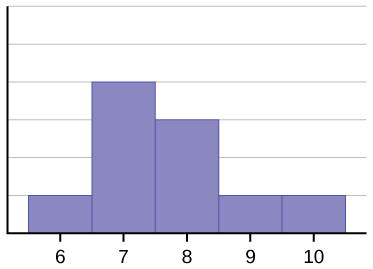
Der Mittelwert ist 7,7, der Median ist 7,5 und der Modus ist sieben. Von den drei Statistiken ist der Mittelwert der größte, während der Modus der kleinste ist. Auch hier spiegelt der Mittelwert die Schieflage am stärksten wider.

Zusammenfassend lässt sich sagen, dass bei einer linksschiefen Verteilung der Daten der Mittelwert im Allgemeinen kleiner ist als der Median, der wiederum oft kleiner ist als der Modus. Wenn die Verteilung der Daten nach rechts schief ist, ist der Modus oft kleiner als der Median, der wiederum kleiner als der Mittelwert ist.

Wie für den Mittelwert, den Median und den Modus und, wie wir gleich sehen werden, die Varianz, gibt es mathematische Formeln, die uns genaue Maße für diese Merkmale der Datenverteilung liefern. Wenn wir uns die Formel für die Schiefe noch einmal ansehen, sehen wir, dass es sich um eine Beziehung zwischen dem Mittelwert der Daten und den einzelnen Beobachtungen kubiert handelt.

wobei die Stichproben-Standardabweichung der Daten, und das arithmetische Mittel und der Stichprobenumfang ist.

Formell ist das arithmetische Mittel als das erste Moment der Verteilung bekannt. Das zweite Moment, das wir sehen werden, ist die Varianz, und die Schiefe ist das dritte Moment. Die Varianz misst die quadrierten Abweichungen der Daten vom Mittelwert und die Schiefe misst die kubierten Abweichungen der Daten vom Mittelwert. Während die Varianz niemals eine negative Zahl sein kann, kann die Schiefe eine negative Zahl sein, und auf diese Weise lässt sich feststellen, ob die Daten rechts- oder linksschief sind. Bei einer Normalverteilung ist die Schiefe gleich Null, und alle symmetrischen Daten sollten eine Schiefe nahe Null aufweisen. Negative Werte für die Schiefe zeigen an, dass die Daten linksschief sind, und positive Werte für die Schiefe zeigen an, dass die Daten rechtsschief sind. Mit linksschief ist gemeint, dass der linke Schwanz im Verhältnis zum rechten Schwanz lang ist. Entsprechend bedeutet schief rechts, dass der rechte Schwanz im Verhältnis zum linken lang ist. Die Schiefe charakterisiert den Grad der Asymmetrie einer Verteilung um ihren Mittelwert. Während der Mittelwert und die Standardabweichung dimensionale Größen sind (deshalb nehmen wir die Quadratwurzel aus der Varianz), d. h. dieselben Einheiten haben wie die gemessenen Größen , wird die Schiefe üblicherweise so definiert, dass sie dimensionslos ist. Sie ist eine reine Zahl, die nur die Form der Verteilung charakterisiert. Ein positiver Wert der Schiefe bedeutet eine Verteilung mit einem asymmetrischen Schwanz, der sich zu einem positiveren X hin ausdehnt, und ein negativer Wert bedeutet eine Verteilung, deren Schwanz sich zu einem negativeren X hin ausdehnt. Ein Maß von Null für die Schiefe zeigt eine symmetrische Verteilung an.

Schiefe und Symmetrie werden wichtig, wenn wir in späteren Kapiteln Wahrscheinlichkeitsverteilungen diskutieren.