Es gibt verschiedene Arten von Graphen, abhängig von der Anzahl der Knoten, der Anzahl der Kanten, der Vernetzbarkeit und ihrer Gesamtstruktur. Wir werden in diesem Kapitel nur einige wenige wichtige Arten von Graphen besprechen.
Null-Graph
Ein Graph, der keine Kanten hat, wird als Null-Graph bezeichnet.
Beispiel

In dem obigen Graphen gibt es drei Scheitelpunkte mit den Namen ‚a‘, ‚b‘ und ‚c‘, aber es gibt keine Kanten zwischen ihnen. Daher ist es ein Nullgraph.
Trivialgraph
Ein Graph mit nur einem Scheitelpunkt wird Trivialgraph genannt.
Beispiel
In dem oben gezeigten Graphen gibt es nur einen Scheitelpunkt ‚a‘ und keine anderen Kanten. Daher ist es ein trivialer Graph.
Nicht gerichteter Graph
Ein nicht gerichteter Graph enthält Kanten, aber die Kanten sind nicht gerichtet.
Beispiel
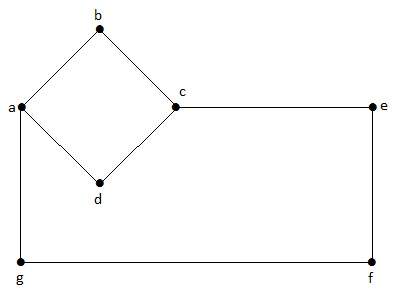
In diesem Graphen sind ‚a‘, ‚b‘, ‚c‘, ‚d‘, ‚e‘, ‚f‘, ‚g‘ die Eckpunkte und ‚ab‘, ‚bc‘, ‚cd‘, ‚da‘, ‚ag‘, ‚gf‘, ‚ef‘ die Kanten des Graphen. Da es sich um einen ungerichteten Graphen handelt, sind die Kanten ‚ab‘ und ‚ba‘ gleich. Auch die anderen Kanten werden auf die gleiche Weise betrachtet.
Gerichteter Graph
In einem gerichteten Graphen hat jede Kante eine Richtung.
Beispiel
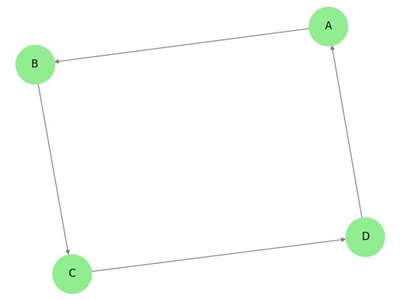
In dem obigen Graphen haben wir sieben Eckpunkte ‚a‘, ‚b‘, ‚c‘, ‚d‘, ‚e‘, ‚f‘ und ‚g‘ und acht Kanten ‚ab‘, ‚cb‘, ‚dc‘, ‚ad‘, ‚ec‘, ‚fe‘, ‚gf‘ und ‚ga‘. Da es sich um einen gerichteten Graphen handelt, ist jede Kante mit einem Pfeil gekennzeichnet, der ihre Richtung angibt. Man beachte, dass in einem gerichteten Graphen ‚ab‘ anders ist als ‚ba‘.
Ein einfacher Graph
Ein Graph ohne Schleifen und ohne parallele Kanten heißt einfacher Graph.
-
Die maximal mögliche Anzahl von Kanten in einem einzelnen Graphen mit ’n‘ Knoten ist nC2, wobei nC2 = n(n – 1)/2.
-
Die Anzahl der möglichen einfachen Graphen mit ’n‘ Scheitelpunkten ist 2nc2 = 2n(n-1)/2.
Beispiel
In dem folgenden Graphen gibt es 3 Scheitelpunkte mit 3 Kanten, was das Maximum ohne die parallelen Kanten und Schleifen ist. Dies kann mit Hilfe der obigen Formeln bewiesen werden.
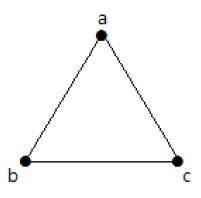
Die maximale Anzahl von Kanten mit n=3 Scheitelpunkten –
nC2 = n(n–1)/2 = 3(3–1)/2 = 6/2 = 3 edges
Die maximale Anzahl von einfachen Graphen mit n=3 Scheitelpunkten –
2nC2 = 2n(n-1)/2 = 23(3-1)/2 = 23 = 8
Diese 8 Graphen sind wie folgt dargestellt –
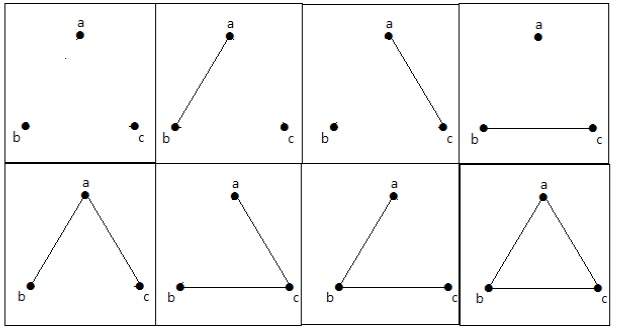
Verbundener Graph
Ein Graph G heißt verbunden, wenn es einen Pfad zwischen jedem Paar von Scheitelpunkten gibt. Für jeden Knoten im Graphen sollte es mindestens eine Kante geben. So dass man sagen kann, dass er mit einem anderen Scheitelpunkt auf der anderen Seite der Kante verbunden ist.
Beispiel
In dem folgenden Graphen hat jeder Scheitelpunkt seine eigene Kante, die mit einer anderen Kante verbunden ist. Es ist also ein zusammenhängender Graph.
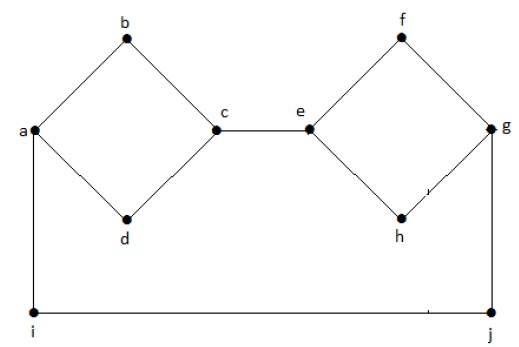
Unzusammenhängender Graph
Ein Graph G ist unzusammenhängend, wenn er nicht mindestens zwei zusammenhängende Knoten enthält.
Beispiel 1
Der folgende Graph ist ein Beispiel für einen unverbundenen Graphen, bei dem es zwei Komponenten gibt, eine mit ‚a‘, ‚b‘, ‚c‘, ‚d‘ Scheitelpunkten und eine andere mit ‚e‘, ‚f‘, ‚g‘, ‚h‘ Scheitelpunkten.
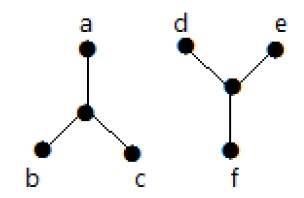
Die beiden Komponenten sind unabhängig und nicht miteinander verbunden. Daher nennt man es einen unverbundenen Graphen.
Beispiel 2
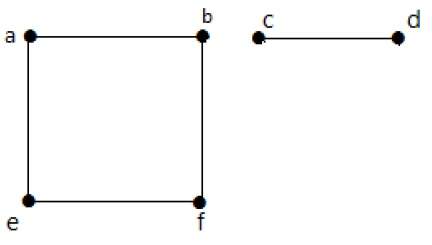
In diesem Beispiel gibt es zwei unabhängige Komponenten, a-b-f-e und c-d, die nicht miteinander verbunden sind. Es handelt sich also um einen unverbundenen Graphen.
Regulärer Graph
Ein Graph G heißt regulär, wenn alle seine Eckpunkte den gleichen Grad haben. Wenn in einem Graphen der Grad eines jeden Scheitelpunktes ‚k‘ ist, dann nennt man den Graphen einen ‚k-regulären Graphen‘.
Beispiel
In den folgenden Graphen haben alle Scheitelpunkte den gleichen Grad. Deshalb nennt man diese Graphen reguläre Graphen.
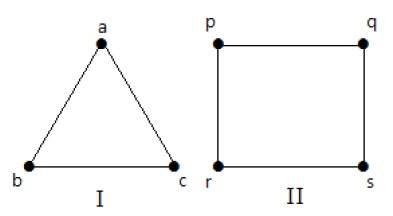
In beiden Graphen haben alle Scheitelpunkte den Grad 2. Sie werden 2-Regular Graphen genannt.
Vollständiger Graph
Ein einfacher Graph mit ’n‘ gegenseitigen Scheitelpunkten wird ein vollständiger Graph genannt und mit ‚Kn‘ bezeichnet. Wenn ein Scheitelpunkt mit allen anderen Scheitelpunkten verbunden ist, nennt man ihn einen vollständigen Graphen.
Mit anderen Worten, wenn ein Scheitelpunkt mit allen anderen Scheitelpunkten in einem Graphen verbunden ist, nennt man ihn einen vollständigen Graphen.
Beispiel
In den folgenden Graphen ist jeder Scheitelpunkt mit allen anderen Scheitelpunkten im Graphen verbunden, außer mit sich selbst.
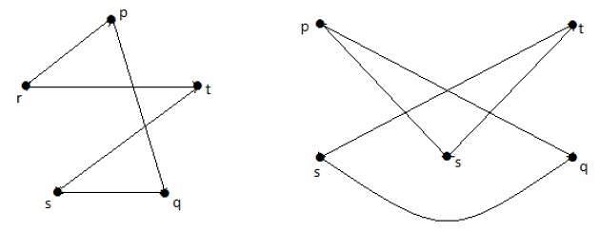
In Graph I,
| a | b | c | |
|---|---|---|---|
| a | Nicht verbunden | Verbunden | Verbunden |
| b | Verbunden | Nicht verbunden | Verbunden |
| c | Verbunden | Verbunden | Nicht verbunden |
In Graph II,
| p | q | r | s | |
|---|---|---|---|---|
| p | Nicht Verbunden | Verbunden | Verbunden | Verbunden |
| q | Verbunden | Nicht Verbunden | Verbunden | Verbunden |
| r | Verbunden | Verbunden | Nicht Verbunden | Verbunden |
| s | Verbunden | Verbunden | Verbunden | Nicht Verbunden |
Zyklusgraph
Ein einfacher Graph mit ’n‘ Knoten (n >= 3) und ’n‘ Kanten heißt ein Zyklusgraph, wenn alle seine Kanten einen Zyklus der Länge ’n‘ bilden.
Wenn der Grad jedes Scheitelpunktes im Graphen zwei ist, dann nennt man ihn einen Zyklusgraphen.
Notation – Cn
Beispiel
Betrachten wir die folgenden Graphen –
-
Graph I hat 3 Scheitelpunkte mit 3 Kanten, die einen Zyklus ‚ab-bc-ca‘ bilden.
-
Graph II hat 4 Eckpunkte mit 4 Kanten, die einen Zyklus ‚pq-qs-sr-rp‘ bilden.
-
Graph III hat 5 Eckpunkte mit 5 Kanten, die einen Zyklus ‚ik-km-ml-lj-ji‘ bilden.
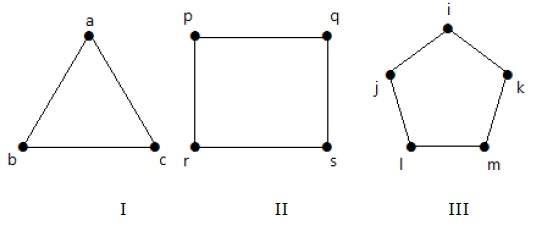
Alle gegebenen Graphen sind also Zyklusgraphen.
Radgraph
Ein Radgraph wird aus einem Zyklusgraphen Cn-1 durch Hinzufügen eines neuen Scheitelpunktes erhalten. Dieser neue Knoten wird Nabe genannt und ist mit allen Knoten von Cn verbunden.
Notation – Wn
No. of edges in Wn = No. of edges from hub to all other vertices + No. of edges from all other nodes in cycle graph without a hub. = (n–1) + (n–1) = 2(n–1)
Beispiel
Schauen Sie sich die folgenden Graphen an. Sie sind alle Radgraphen.
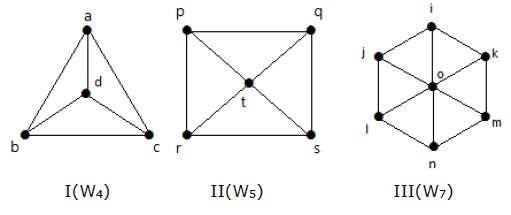
In Graph I wird er aus C3 durch Hinzufügen eines Scheitelpunkts in der Mitte mit der Bezeichnung „d“ gewonnen. Es wird als W4 bezeichnet.
Number of edges in W4 = 2(n-1) = 2(3) = 6
In Diagramm II wird es aus C4 durch Hinzufügen eines Scheitelpunktes in der Mitte mit der Bezeichnung „t“ erhalten. Es wird als W5.
Number of edges in W5 = 2(n-1) = 2(4) = 8
bezeichnet. In Diagramm III wird es aus C6 durch Hinzufügen eines Scheitelpunkts in der Mitte mit der Bezeichnung „o“ erhalten. Er wird als W7 bezeichnet.
Number of edges in W4 = 2(n-1) = 2(6) = 12
Zyklischer Graph
Ein Graph mit mindestens einem Zyklus wird als zyklischer Graph bezeichnet.
Beispiel
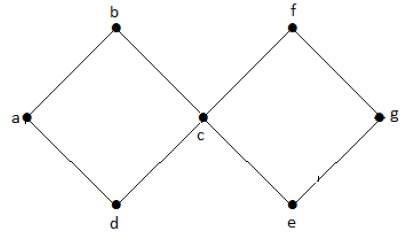
In dem obigen Beispielgraph gibt es zwei Zyklen a-b-c-d-a und c-f-g-e-c. Daher nennt man ihn einen zyklischen Graphen.
Azyklischer Graph
Einen Graphen ohne Zyklen nennt man einen azyklischen Graphen.
Beispiel
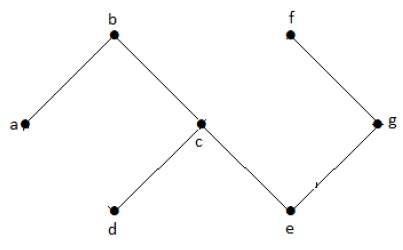
In dem obigen Beispielgraphen gibt es keine Zyklen. Daher ist er ein nicht-zyklischer Graph.
Zweigliedriger Graph
Ein einfacher Graph G = (V, E) mit der Knotenpartition V = {V1, V2} heißt ein zweigliedriger Graph, wenn jede Kante von E einen Knoten in V1 mit einem Knoten in V2 verbindet.
Im Allgemeinen hat ein bipartiter Graph zwei Mengen von Scheitelpunkten, sagen wir V1 und V2, und wenn eine Kante gezeichnet wird, sollte sie jeden Scheitelpunkt in der Menge V1 mit jedem Scheitelpunkt in der Menge V2 verbinden.
Beispiel
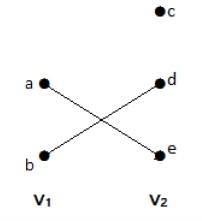
In diesem Graphen kann man zwei Mengen von Scheitelpunkten beobachten – V1 und V2. Hier verbinden zwei Kanten mit den Namen ‚ae‘ und ‚bd‘ die Scheitelpunkte der beiden Mengen V1 und V2.
Vollständiger zweistufiger Graph
Ein zweistufiger Graph ‚G‘, G = (V, E) mit der Partition V = {V1, V2} wird als vollständiger zweistufiger Graph bezeichnet, wenn jeder Scheitelpunkt in V1 mit jedem Scheitelpunkt von V2 verbunden ist.
Im Allgemeinen verbindet ein vollständiger bipartiter Graph jeden Scheitelpunkt aus der Menge V1 mit jedem Scheitelpunkt aus der Menge V2.
Beispiel
Der folgende Graph ist ein vollständiger bipartiter Graph, weil er Kanten hat, die jeden Scheitelpunkt aus der Menge V1 mit jedem Scheitelpunkt aus der Menge V2 verbinden.
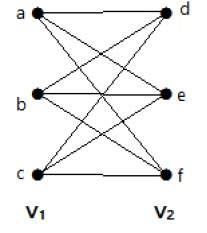
Wenn |V1| = m und |V2| = n, dann wird der vollständige bipartite Graph mit Km, n bezeichnet.
-
Km,n hat (m+n) Knoten und (mn) Kanten.
-
Km,n ist ein regulärer Graph, wenn m=n.
Im Allgemeinen ist ein vollständiger bipartiter Graph kein vollständiger Graph.
Km,n ist ein vollständiger Graph, wenn m=n=1.
Die maximale Anzahl der Kanten in einem zweiseitigen Graphen mit n Knoten ist
Wenn n=10, k5, 5= ⌊n2/4⌋ = ⌊102/4⌋ = 25
Also K6, 4=24
K7, 3=21
K8, 2=16
K9, 1=9
Wenn n=9, k5, 4 = ⌊n2/4⌋ = ⌊92/4⌋ = 20
Also K6, 3=18
K7, 2=14
K8, 1=8
‚G‘ ist ein bipartiter Graph, wenn ‚G‘ keine Zyklen von ungerader Länge hat. Ein Spezialfall eines bipartiten Graphen ist ein Sterngraph.
Sterngraph
Ein vollständiger bipartiter Graph der Form K1, n-1 ist ein Sterngraph mit n-Vertikeln. Ein Sterndiagramm ist ein vollständiges bipartites Diagramm, wenn ein einziger Scheitelpunkt zu einer Menge gehört und alle übrigen Scheitelpunkte zu der anderen Menge gehören.
Beispiel
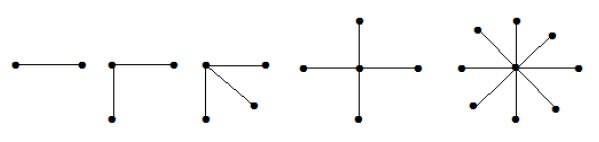
In den obigen Diagrammen sind von den „n“ Scheitelpunkten alle „n-1“ Scheitelpunkte mit einem einzigen Scheitelpunkt verbunden. Daher ist es in der Form von K1, n-1, die Sterngraphen sind.
Komplement eines Graphen
Lassen Sie ‚G-‚ einen einfachen Graphen mit einigen Scheitelpunkten wie die von ‚G‘ sein und eine Kante {U, V} ist in ‚G-‚ vorhanden, wenn die Kante nicht in G vorhanden ist. Das bedeutet, dass zwei Scheitelpunkte in ‚G-‚ benachbart sind, wenn die beiden Scheitelpunkte in G nicht benachbart sind.
Wenn die Kanten, die im Graphen I vorhanden sind, in einem anderen Graphen II fehlen, und wenn sowohl der Graph I als auch der Graph II zusammen einen vollständigen Graphen bilden, dann nennt man den Graphen I und den Graph II Komplemente voneinander.
Beispiel
Im folgenden Beispiel hat der Graph I zwei Kanten ‚cd‘ und ‚bd‘. Sein Komplement Graph-II hat vier Kanten.
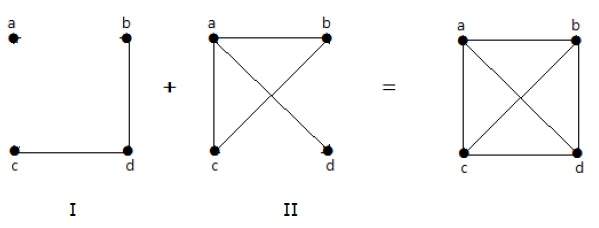
Beachte, dass die Kanten in Graph-I nicht in Graph-II vorhanden sind und umgekehrt. Daher ergibt die Kombination beider Graphen einen vollständigen Graphen mit ’n‘ Scheitelpunkten.
Anmerkung – Eine Kombination zweier komplementärer Graphen ergibt einen vollständigen Graphen.
Wenn ‚G‘ ein beliebiger einfacher Graph ist, dann
|E(G)| + |E(‚G-‚)| = |E(Kn)|, wobei n = Anzahl der Scheitelpunkte im Graphen.
Beispiel
Sei ‚G‘ ein einfacher Graph mit neun Scheitelpunkten und zwölf Kanten, finde die Anzahl der Kanten in ‚G-‚.
Sie haben, |E(G)| + |E(‚G-‚)| = |E(Kn)|
12 + |E(‚G-‚)| =