2.972 Wie ein Tragflächenboot funktioniert

HYDROFOILS
FRAGEN ODER KOMMENTARE
Vor & Nach 2.972	AUTHOR:	Tina Rosado
	E-MAIL:	[email protected]
	COURSE:	2
	KLASSE/JAHR:	2

HAUPTFUNKTIONALE ANFORDERUNG: Heben Sie den Bootsrumpf aus dem Wasser.

DESIGN PARAMETER: Hydrofoil(Es ist eine Folie oder Flügel unter Wasser verwendet, um den Bootsrumpf zu heben, bis es vollständig außerhalb des Wassers ist.)

GEOMETRIE/STRUKTUR:

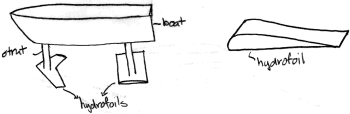
Detail der Tragflächengeometrie

ERKLÄRUNG WIE ES FUNKTIONIERT/ANGEWENDET WIRD:

1. Bei niedrigen Geschwindigkeiten liegt der Rumpf (Schiffskörper) im Wasser und die Tragflächen sind vollständig in das Wasser eingetaucht.

2. Wenn die Geschwindigkeit des Bootes zunimmt, erzeugen die Tragflächen einen Auftrieb.

3. Bei einer bestimmten Geschwindigkeit ist der von den Tragflächen erzeugte Auftrieb gleich der Summe der Gewichte von Boot und Ladung. Dadurch wird der Rumpf aus dem Wasser gehoben.

4. Anstatt dass der Luftwiderstand mit zunehmender Geschwindigkeit zunimmt, weil der Rumpf aus dem Wasser gehoben wird (im Gegensatz zu herkömmlichen Booten aufgrund des Druckwiderstands), bieten die Tragflächen eine effizientere Art der Fortbewegung. Die Verringerung des Luftwiderstands trägt dazu bei, die für die Bewegung des Bootes benötigte Kraft besser zu nutzen.

DOMINANT PHYSICS:

Wie entsteht der Auftrieb – Fluid Dynamics.

Für dieses Projekt werden zwei Erklärungen in allgemeiner und grundlegender Form vorgestellt. Diese Theorien sind die Anwendung der Bernoullis-Gleichung und der Eulers-Gleichung für den Stromlinienkrümmungseffekt.

Bernoullis-Gleichung: Po = P1 + ½

rv1² + rgy1 = P2 + ½rv2² + rgy2

Variablen	Einheiten
Po Stagnationsdruck	oder
P Druck	oder
r Dichte	oder
V Geschwindigkeit	oder
g Gravitationskonstante	oder
y Höhe	oder

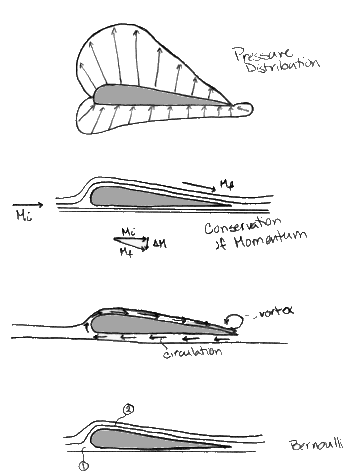
Detail des Tragflügels: a) Druckprofil b) Impulsübertragung c) Zirkulation d) Stromlinien

Diese Gleichung gilt für Strömungen entlang einer Stromlinie, die als: nicht viskos, inkompressibel, stationär, irrotierend und für die die Körperkräfte konservativ sind, modelliert werden können. Auch die Höhendifferenz der Folie (der Abstand zwischen dem unteren und dem oberen Abschnitt) ist so klein, dass die Differenz rgy2 – rgy1 im Vergleich zur Differenz der übrigen Terme vernachlässigbar ist. Es bleibt übrig, dass der Druck plus die halbe Dichte mal die Geschwindigkeit zum Quadrat eine Konstante (den Staudruck) ergibt.
Mit zunehmender Geschwindigkeit entlang dieser Stromlinien sinkt der Druck (dies wird in Kürze wichtig werden). Die Flüssigkeit, die sich über die Oberseite der Folie bewegt, bewegt sich schneller als die Flüssigkeit auf der Unterseite. Um den Drehimpuls zu erhalten, der durch die Rotation der Wirbel gegen den Uhrzeigersinn verursacht wird, muss ein gleicher, aber entgegengesetzter Impulsaustausch mit dem Wirbel an der Hinterkante der Folie stattfinden. Dies führt zu einer Zirkulation des Fluids um die Folie. Die vektorielle Summierung der Geschwindigkeiten ergibt eine höhere Geschwindigkeit auf der Oberseite und eine geringere Geschwindigkeit auf der Unterseite, was bei Bernoullis dazu führt, dass die Geschwindigkeitsänderung beim Durchschneiden des Fluids den für den Auftrieb erforderlichen Druckabfall erzeugt. Wie im Diagramm dargestellt, ist die resultierende oder Nettokraft (Kraft= (Druck)(Fläche)) nach oben gerichtet. Diese Erklärung kann durch den Impulserhaltungssatz ergänzt werden (Impuls = (Masse)(Geschwindigkeit)). Wenn die Geschwindigkeit eines Teilchens mit einem Anfangsimpuls erhöht wird, gibt es einen Gegenimpuls, der gleich groß und entgegengesetzt zur Differenz der Impulse ist. (Siehe Diagramm).(Mi = Mf + DM)

Eulers Gleichung: d(p+rgy)/dn = rv²/R

Variablen	Einheiten
P Druck	oder
r Dichte	oder
V Geschwindigkeit	oder
g Gravitationskonstante	oder
y Höhe	oder
n Vektor in Radialrichtung	—
R Krümmungsradius der Stromlinie	oder

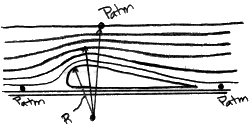
Detail des Drucks an Punkten über einem Tragflächenprofil

Hier wieder, wird der Term, der sich auf die Höhe bezieht, im Vergleich zu den anderen Termen der Gleichung als vernachlässigbar angenommen. Diese Gleichung besagt, dass der Druck auf die Stromlinien zunimmt, je weiter man sich vom Mittelpunkt des Krümmungsradius einer Stromlinie entfernt. Die Oberseite der Folie liegt näher am Krümmungsmittelpunkt der Stromlinien, daher ist der Druck über der Folie geringer als der Umgebungsdruck. Die Differenz zwischen dem Druck an der Oberseite und dem Umgebungsdruck an der Unterseite erzeugt einen Nettodruck, der den Auftrieb verursacht.(Seediagramm.)

Anstellwinkel:

Anstellwinkel

Wie bereits dargestellt, entsteht der Auftrieb durch die Dynamik des Fluids in den Bereichen um die Folie herum. Der Auftrieb kann jedoch optimiert werden, indem das Tragflächenprofil in einem Winkel (relativ zur einströmenden Flüssigkeit) positioniert wird, der Anstellwinkel genannt wird (siehe Diagramm). Ziel ist es, das Verhältnis zwischen Auftrieb und Widerstand zu optimieren. Dieses Verhältnis hängt von der Form der Folie ab, die in diesem Fall als dünne Folie betrachtet wird. Bei einem kleinen Anstellwinkel steigt der Auftrieb schnell an, während der Widerstand nur geringfügig zunimmt. Ab einem Winkel von ~10° nimmt der Auftrieb langsam zu, bis er bei ~15° ein Maximum erreicht. Nach ~15° kann der Strömungsabriss eintreten. Bei einem Anstellwinkel von 3° bis 4° ist das Verhältnis von Auftrieb zu Widerstand am größten.Daher ist das Profil bei diesen Winkeln (3° und 4°) mit einem Verhältnis von Auftrieb zu Widerstand von ~ 20 bis 25:1 effizienter

EINSCHRÄNKENDE PHYSIK:

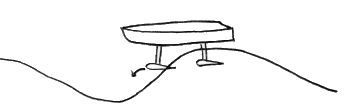
Detail der Tragflächengeometrie

Auf den ersten Blick könnte man meinen, dass der Strömungsabriss bei Tragflächenprofilen ebenso ein Problem darstellt wie bei Tragflügeln, aber überraschenderweise ist das nicht der Fall. Ein steiler Anstellwinkel ist für die Konstruktion des Tragflügels nicht erforderlich. Im Gegenteil, kleine Anstellwinkel werden bei Tragflächenprofilen verwendet, um das Verhältnis von Auftrieb zu Widerstand zu optimieren, wie bereits erläutert.

Das Hauptaugenmerk liegt auf der Konstruktion des Tragflügels, den Verstrebungen/Stützen und deren Positionierung. Alle diese Merkmale müssen berücksichtigt werden. Die Eigenschaften sind also so ausgelegt, dass eine Mindestgeschwindigkeit erreicht wird, die das Boot mit einem bestimmten Gewicht anhebt und es auf dem Profil hält.

Ein Problem, das bei einem Tragflächenboot auftreten kann, ist die Höhe der Wellen, die größer ist als die Streben. Wenn das Boot schneller fährt als die Wellen, können die Tragflächen an der Oberfläche und außerhalb des Wassers brechen, was zu einem Verlust an Auftrieb und einem negativen Anstellwinkel führt, wenn das Boot in die nächste Welle eintaucht, so dass es ins Meer stürzt. Ingenieure haben Tragflächen entworfen, um diese Einschränkungen zu minimieren und die Leistung der Schiffe zu verbessern.

PLOTS/GRAPHEN/TABELLEN:

Keine eingereicht

Einige Tragflächen und ihre Verwendung:

Hydrofolien sind sehr beliebt geworden. Sie werden für verschiedene Arten von Seereisen verwendet, vom militärischen Einsatz bis zum Wassersport. Die hohe Geschwindigkeit, die ruhige Fahrt und die besseren Kurvenfahrten von Tragflächenbooten werden in Militärschiffen genutzt. Auch im Segelsport werden Tragflächenboote eingesetzt, um eine höhere Geschwindigkeit zu erreichen. Sie ermöglichen neue Erfindungen, die das Bedürfnis der Menschen befriedigen können, sich der Gefahr zu stellen, wie z. B. der Sky Ski. Dabei handelt es sich um einen Wasserski, an dem ein Tragflächenboot befestigt ist, mit dem man über die Wasseroberfläche fliegen kann. Jeden Tag werden mehr Tragflächenboote eingesetzt, und in der Zukunft könnten sie die vorherrschende Methode der Fortbewegung auf dem Wasser sein.

REFERENZEN/weitere Informationen:

Siehe auch auf dieser Seite: Tragflächen, Segelboote

Alexander, Alan, James Grogono, und Donald Nigg; Hydrofoil Sailing. JuanitaKalerghi: London, 1972.

Bertin, John und Michael Smith; Aerodynamics for Engineers, Third Ediotion.Prentice Hall: New Jersey, 1998.

Hook, Cristopher und A.C. Kermode; Hydrofoils. Pitman Paperbags: London, 1967.

The International Hydrofoil Societys Web Page:http://www.erols.com/foiler/index.html