Există diferite tipuri de grafuri în funcție de numărul de vârfuri, numărul de muchii, interconectivitatea și structura lor generală. Vom discuta doar câteva tipuri importante de grafuri în acest capitol.
Grafic nul
Un graf care nu are muchii se numește graf nul.
Exemplu

În graful de mai sus, există trei vârfuri numite „a”, „b” și „c”, dar nu există muchii între ele. Prin urmare, este un graf nul.
Graf trivial
Un graf cu un singur vârf se numește graf trivial.
Exemplu
În graficul prezentat mai sus, există un singur vârf ‘a’ fără alte muchii. Prin urmare, este un graf trivial.
Graf neorientat
Un graf neorientat conține muchii, dar muchiile nu sunt direcționate.
Exemplu
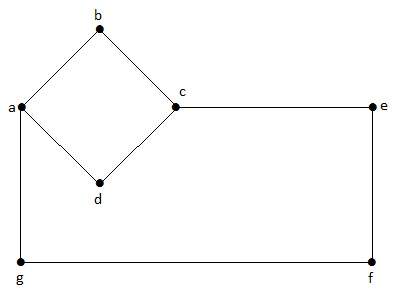
În acest graf, ‘a’, ‘b’, ‘c’, ‘d’, ‘e’, ‘f’, ‘g’ sunt vârfurile, iar ‘ab’, ‘bc’, ‘cd’, ‘da’, ‘ag’, ‘gf’, ‘ef’ sunt muchii ale grafului. Deoarece este un graf nedirijat, marginile „ab” și „ba” sunt identice. În mod similar, și celelalte muchii sunt considerate în același mod.
Grafic dirijat
Într-un graf dirijat, fiecare muchie are o direcție.
Exemplu
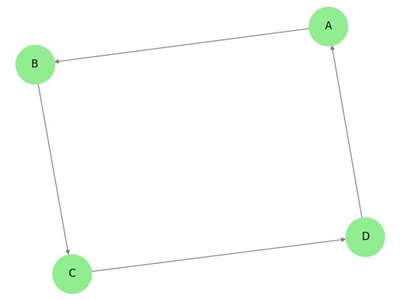
În graful de mai sus, avem șapte vârfuri „a”, „b”, „c”, „d”, „e”, „f”, și „g”, și opt muchii „ab”, „cb”, „dc”, „ad”, „ec”, „fe”, „gf”, și „ga”. Deoarece este un graf direcționat, fiecare muchie poartă un semn de săgeată care indică direcția sa. Rețineți că într-un graf dirijat, ‘ab’ este diferit de ‘ba’.
Graf simplu
Un graf fără bucle și fără muchii paralele se numește graf simplu.
-
Numărul maxim de muchii posibile într-un singur graf cu ‘n’ vârfuri este nC2, unde nC2 = n(n – 1)/2.
-
Numărul de grafuri simple posibile cu ‘n’ vârfuri = 2nc2 = 2n(n-1)/2.
Exemplu
În următorul graf, există 3 vârfuri cu 3 muchii care este maxim excluzând muchii paralele și bucle. Acest lucru poate fi demonstrat folosind formulele de mai sus.
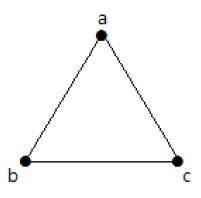
Numărul maxim de muchii cu n=3 vârfuri –
nC2 = n(n–1)/2 = 3(3–1)/2 = 6/2 = 3 edges
Numărul maxim de grafuri simple cu n=3 vârfuri –
2nC2 = 2n(n-1)/2 = 23(3-1)/2 = 23 = 8
Aceste 8 grafuri sunt așa cum se arată mai jos –
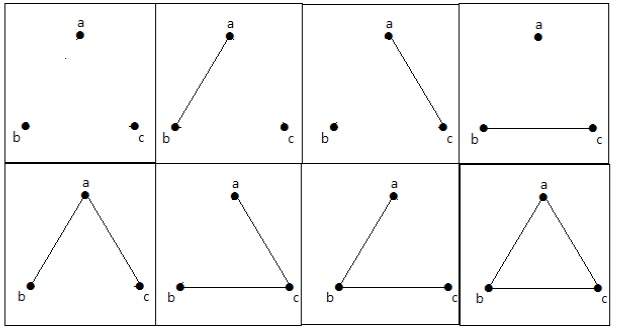
Grafic conex
Un graf G se spune că este conex dacă există o cale între fiecare pereche de vârfuri. Trebuie să existe cel puțin o muchie pentru fiecare vârf din graf. Astfel încât să putem spune că acesta este conectat cu un alt vârf aflat de cealaltă parte a muchiei.
Exemplu
În următorul graf, fiecare vârf are o muchie proprie conectată cu o altă muchie. Prin urmare, este un graf conex.
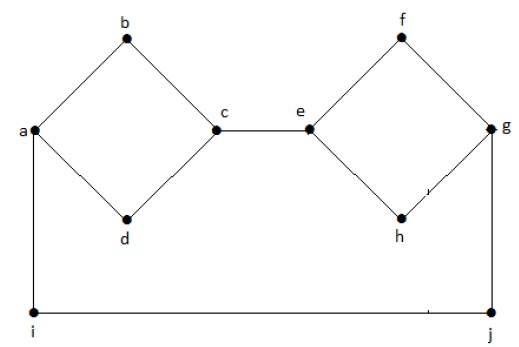
Graf deconectat
Un graf G este deconectat, dacă nu conține cel puțin două vârfuri conectate.
Exemplu 1
Graficul următor este un exemplu de Graf Deconectat, în care există două componente, una cu vârfurile „a”, „b”, „c”, „d” și alta cu vârfurile „e”, „f”, „g”, „h”.
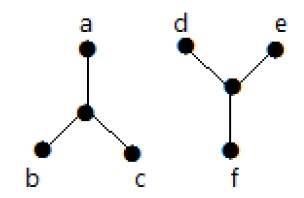
Cele două componente sunt independente și nu sunt conectate între ele. Prin urmare, se numește graf deconectat.
Exemplu 2
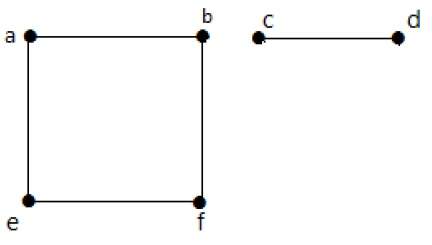
În acest exemplu, există două componente independente, a-b-f-e și c-d, care nu sunt conectate între ele. Prin urmare, acesta este un graf deconectat.
Grafic regulat
Un graf G se spune că este regulat, dacă toate vârfurile sale au același grad. Într-un graf, dacă gradul fiecărui vârf este „k”, atunci graful se numește „graf k-regular”.
Exemplu
În următoarele grafuri, toate vârfurile au același grad. Deci aceste grafuri se numesc grafuri regulate.
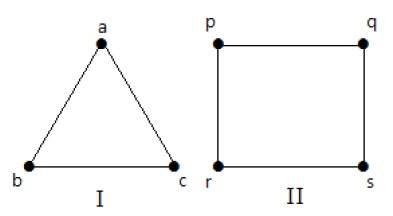
În ambele grafuri, toate vârfurile au gradul 2. Ele se numesc grafuri 2-regulare.
Graf complet
Un graf simplu cu „n” vârfuri comune se numește graf complet și se notează cu „Kn”. În graf, un vârf trebuie să aibă muchii cu toate celelalte vârfuri, atunci se numește graf complet.
Cu alte cuvinte, dacă un vârf este conectat cu toate celelalte vârfuri dintr-un graf, atunci acesta se numește graf complet.
Exemplu
În următoarele grafuri, fiecare vârf din graf este conectat cu toate celelalte vârfuri din graf, cu excepția lui însuși.
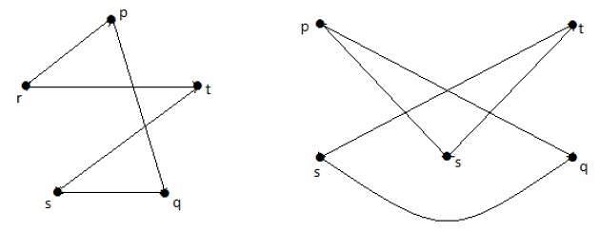
În graficul I,
| a | b | c | ||
|---|---|---|---|---|
| a | Nu sunt conectate | Conectate | Conectate | |
| b | Connected | Not Connected | Connected | |
| c | Connected | Connected | Connected | Not Connected |
În graficul II,
| p | q | r | s | ||
|---|---|---|---|---|---|
| p | Nu sunt conectate | Conectate | Conectate | Conectate | Connected |
| q | Connected | Not Connected | Connected | Connected | Connected |
| r | Connected | Connected | Connected | Not Connected | Connected |
| s | Connected | Connected | Connected | Connected | Not Conectat |
Graf cu ciclu
Un graf simplu cu „n” vârfuri (n >= 3) și „n” muchii se numește graf cu ciclu dacă toate muchiile sale formează un ciclu de lungime „n”.
Dacă gradul fiecărui vârf din graf este doi, atunci acesta se numește graf ciclic.
Notație – Cn
Exemplu
Consultați următoarele grafuri –
-
Graful I are 3 vârfuri cu 3 muchii care formează un ciclu ‘ab-bc-ca’.
-
Graficul II are 4 vârfuri cu 4 muchii care formează un ciclu ‘pq-qs-sr-rp’.
-
Graficul III are 5 vârfuri cu 5 muchii care formează un ciclu ‘ik-km-ml-lj-ji’.
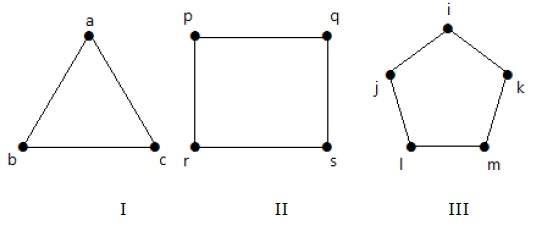
Înseamnă că toate grafurile date sunt grafuri ciclice.
Graficul roată
Un graf roată se obține dintr-un graf ciclic Cn-1 prin adăugarea unui nou vârf. Acest nou vârf se numește Hub care este conectat cu toate vârfurile din Cn.
Notație – Wn
No. of edges in Wn = No. of edges from hub to all other vertices + No. of edges from all other nodes in cycle graph without a hub. = (n–1) + (n–1) = 2(n–1)
Exemplu
Consultați următoarele grafuri. Toate sunt grafuri de roți.
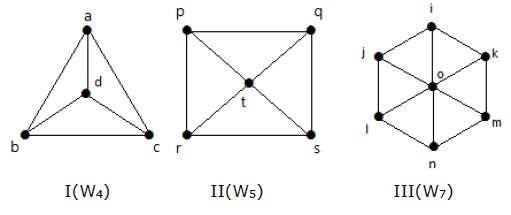
În graficul I, acesta se obține din C3 prin adăugarea unui vertex la mijloc numit „d”. Se notează ca W4.
Number of edges in W4 = 2(n-1) = 2(3) = 6
În graficul II, acesta se obține din C4 prin adăugarea unui vârf la mijloc numit ‘t’. Se notează ca W5.
Number of edges in W5 = 2(n-1) = 2(4) = 8
În graficul III, se obține din C6 prin adăugarea unui vârf la mijloc numit „o”. Se notează ca W7.
Number of edges in W4 = 2(n-1) = 2(6) = 12
Grafic ciclic
Un grafic cu cel puțin un ciclu se numește grafic ciclic.
Exemplu
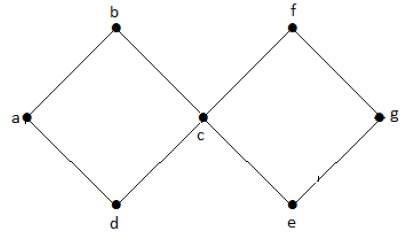
În graficul de exemplu de mai sus, avem două cicluri a-b-c-d-a și c-f-g-e-c. Prin urmare, se numește un graf ciclic.
Graf ciclic
Un graf fără cicluri se numește graf aciclic.
Exemplu
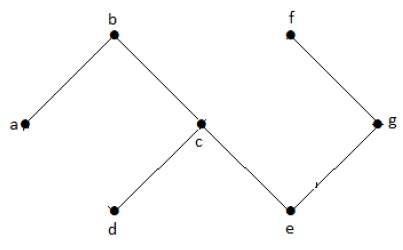
În graful de exemplu de mai sus, nu avem niciun ciclu. Prin urmare, este un graf neciclic.
Graf bipartit
Un graf simplu G = (V, E) cu partiția de vertexuri V = {V1, V2} se numește graf bipartit dacă fiecare muchie din E unește un vertex din V1 cu un vertex din V2.
În general, un graf bipartit are două seturi de vârfuri, să spunem, V1 și V2, iar dacă se trasează o muchie, aceasta trebuie să lege orice vârf din setul V1 cu orice vârf din setul V2.
Exemplu
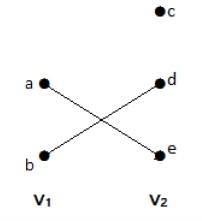
În acest graf, se pot observa două seturi de vârfuri – V1 și V2. Aici, două muchii numite „ae” și „bd” leagă vârfurile celor două seturi V1 și V2.
Graf bipartit complet
Un graf bipartit „G”, G = (V, E) cu partiția V = {V1, V2} se spune că este un graf bipartit complet dacă fiecare vârf din V1 este conectat cu fiecare vârf din V2.
În general, un graf bipartit complet conectează fiecare vârf din setul V1 cu fiecare vârf din setul V2.
Exemplu
Graful următor este un graf bipartit complet deoarece are muchii care conectează fiecare vârf din setul V1 cu fiecare vârf din setul V2.
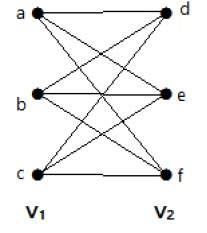
Dacă |V1| = m și |V2| = n, atunci graful bipartit complet se notează cu Km, n.
-
Km,n are (m+n) vârfuri și (mn) muchii.
-
Km,n este un graf regulat dacă m=n.
În general, un graf bipartit complet nu este un graf complet.
Km,n este un graf complet dacă m=n=1.
Numărul maxim de muchii într-un graf bipartit cu n vârfuri este
Dacă n=10, k5, 5= ⌊n2/4⌋ = ⌊102/4⌋ = 25
Similar K6, 4=24
K7, 3=21
K8, 2=16
K9, 1=9
Dacă n=9, k5, 4 = ⌊n2/4⌋ = ⌊92/4⌋ = 20
În mod similar K6, 3=18
K7, 2=14
K8, 1=8
‘G’ este un graf bipartit dacă ‘G’ nu are cicluri de lungime impară. Un caz special de graf bipartit este un graf stelar.
Graf stelar
Un graf bipartit complet de forma K1, n-1 este un graf stelar cu n verigi. Un graf stelar este un graf bipartit complet dacă un singur vârf aparține unui set și toate celelalte vârfuri aparțin celuilalt set.
Exemplu
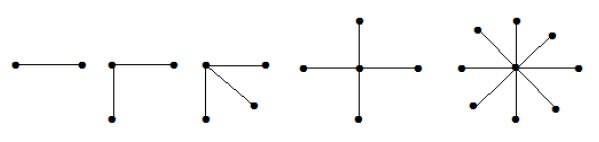
În grafurile de mai sus, din ‘n’ vârfuri, toate cele ‘n-1’ vârfuri sunt conectate la un singur vârf. Prin urmare, are forma K1, n-1, care sunt grafuri stelare.
Complementarul unui graf
Să fie ‘G-‘ un graf simplu cu unele vârfuri ca cele din ‘G’ și o muchie {U, V} este prezentă în ‘G-‘, dacă muchia nu este prezentă în G. Aceasta înseamnă că două vârfuri sunt adiacente în ‘G-‘ dacă cele două vârfuri nu sunt adiacente în G.
Dacă marginile care există în graful I sunt absente într-un alt graf II și dacă atât graful I cât și graful II sunt combinate împreună pentru a forma un graf complet, atunci graful I și graful II se numesc complemente unul altuia.
Exemplu
În următorul exemplu, graful I are două muchii ‘cd’ și ‘bd’. Complementul său graful-II are patru muchii.
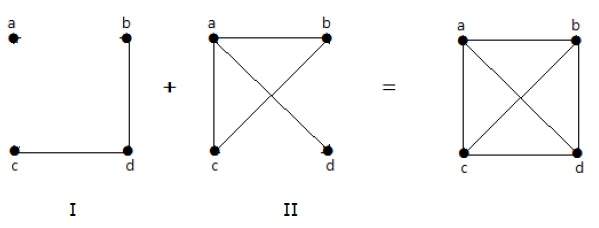
Rețineți că muchiile din graful-I nu sunt prezente în graful-II și viceversa. Prin urmare, combinația celor două grafuri dă un graf complet de ‘n’ vârfuri.
Nota – O combinație a două grafuri complementare dă un graf complet.
Dacă ‘G’ este un graf simplu oarecare, atunci
|E(G)| + |E(‘G-‘)| = |E(Kn)|, unde n = numărul de vârfuri din graf.
Exemplu
După ce ‘G’ este un graf simplu cu nouă vârfuri și douăsprezece muchii, aflați numărul de muchii din ‘G-‘.
Aveți, |E(G)| + |E(‘G-‘)| = |E(Kn)|
12 + |E(‘G-‘)| =
.