Introductory Business Statistics

Considerați următorul set de date.
4; 5; 5; 6; 6; 6; 6; 6; 7; 7; 7; 7; 7; 7; 7; 7; 7; 7; 8; 8; 8; 8; 9; 10

Acest set de date poate fi reprezentat prin următoarea histogramă. Fiecare interval are lățimea unu, iar fiecare valoare este situată în mijlocul unui interval.

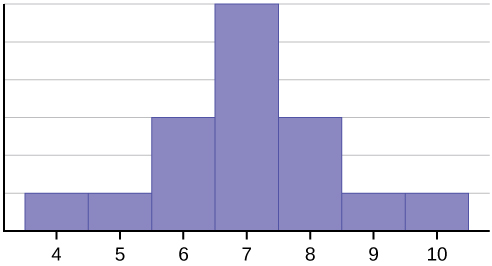
Histograma prezintă o distribuție simetrică a datelor. O distribuție este simetrică dacă la un anumit punct al histogramei se poate trasa o linie verticală astfel încât forma din stânga și din dreapta liniei verticale să fie imagini în oglindă una față de cealaltă. Media, mediana și modul sunt fiecare șapte pentru aceste date. Într-o distribuție perfect simetrică, media și mediana sunt identice. Acest exemplu are un singur mod (unimodal), iar modul este același cu media și mediana. Într-o distribuție simetrică care are două moduri (bimodală), cele două moduri ar fi diferite de medie și mediană.

Histograma pentru aceste date: 456667777778 nu este simetrică. Partea dreaptă pare „tăiată” în comparație cu partea stângă. O distribuție de acest tip se numește înclinată spre stânga, deoarece este trasă spre stânga. Putem măsura în mod formal asimetria unei distribuții, la fel cum putem măsura matematic greutatea centrală a datelor sau „viteza” generală a acestora. Formula matematică pentru asimetrie este: . Cu cât abaterea de la zero este mai mare, cu atât indică un grad mai mare de skewness. Dacă asimetria este negativă, atunci distribuția este înclinată spre stânga, ca în (Figura). O măsură pozitivă a asimetriei indică o asimetrie spre dreapta, cum ar fi (Figura).

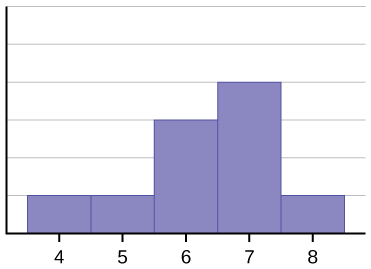
Media este 6,3, mediana este 6,5, iar modul este șapte. Observați că media este mai mică decât mediana, iar ambele sunt mai mici decât modul. Atât media, cât și mediana reflectă înclinarea, dar media o reflectă mai mult.

Histograma pentru date: 67777888910, nu este, de asemenea, simetrică. Ea este înclinată spre dreapta.

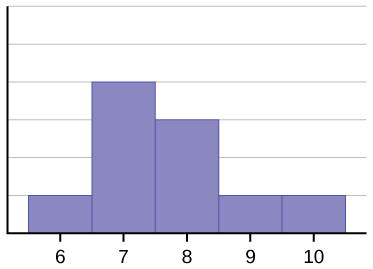
Media este 7,7, mediana este 7,5, iar modul este șapte. Dintre cele trei statistici, media este cea mai mare, în timp ce modul este cel mai mic. Din nou, media reflectă cel mai mult înclinarea.

Pentru a rezuma, în general, dacă distribuția datelor este înclinată spre stânga, media este mai mică decât mediana, care este adesea mai mică decât modul. Dacă distribuția datelor este înclinată spre dreapta, modul este adesea mai mic decât mediana, care este mai mică decât media.

Ca și în cazul mediei, medianei și modului și, după cum vom vedea în curând, a varianței, există formule matematice care ne oferă măsuri precise ale acestor caracteristici ale distribuției datelor. Privind din nou la formula pentru asimetrie, vedem că aceasta este o relație între media datelor și observațiile individuale cuplate.

unde este abaterea standard a eșantionului de date, , iar este media aritmetică și este dimensiunea eșantionului.

În mod normal, media aritmetică este cunoscută ca primul moment al distribuției. Al doilea moment pe care îl vom vedea este varianța, iar asimetria este al treilea moment. Varianța măsoară diferențele pătratice ale datelor față de medie, iar asimetria măsoară diferențele cubice ale datelor față de medie. În timp ce o varianță nu poate fi niciodată un număr negativ, măsura asimetriei poate fi un număr negativ, iar acesta este modul în care determinăm dacă datele sunt înclinate spre dreapta sau spre stânga. Skewness pentru o distribuție normală este zero, iar orice date simetrice ar trebui să aibă skewness aproape de zero. Valorile negative pentru skewness indică date care sunt înclinate spre stânga, iar valorile pozitive pentru skewness indică date care sunt înclinate spre dreapta. Prin „înclinat spre stânga”, ne referim la faptul că coada stângă este lungă în raport cu coada dreaptă. În mod similar, prin „skewed right” se înțelege că coada din dreapta este lungă în raport cu coada din stânga. Asimetria caracterizează gradul de asimetrie a unei distribuții în jurul mediei sale. În timp ce media și abaterea standard sunt mărimi dimensionale (acesta este motivul pentru care vom lua rădăcina pătrată a varianței ), adică au aceleași unități ca și mărimile măsurate , asimetria este definită în mod convențional astfel încât să o facă nondimensională. Ea este un număr pur care caracterizează doar forma distribuției. O valoare pozitivă a asimetriei semnifică o distribuție cu o coadă asimetrică care se extinde spre un X mai pozitiv, iar o valoare negativă semnifică o distribuție a cărei coadă se extinde spre un X mai negativ. o măsură zero a asimetriei va indica o distribuție simetrică.

Asimetria și simetria devin importante atunci când discutăm despre distribuțiile de probabilitate în capitolele ulterioare.

.