La fel ca în cazul unei prăjituri, poți avea 2 bucăți mici sau o bucată de două ori mai mare și este aceeași cantitate. Prin urmare, o mulțime de fracții sunt echivalente, cum ar fi 2/5 și 4/10.


Care număr poate fi scris sub formă de fracție
Scrieți orice număr întreg mai mare de 1 pentru a-l transforma în fracție, deoarece numărul total de părți din orice întreg indivizibil este unu.
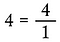
Multiplicați fracții în linie dreaptă
Multiplicarea fracțiilor este ușoară, trebuie doar să înmulțiți în linie dreaptă.
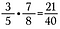
Nota: Numerele mixte trebuie transformate mai întâi în fracții improprii, citiți mai departe pentru mai multe informații despre acest lucru.
Înmulțiți oricând cu orice formă de unu
Numărul 1 se numește identitate multiplicativă pentru că îl putem înmulți cu orice număr și numărul rămâne același. Acest lucru este important pentru fracții, deoarece de multe ori trebuie să modificăm aspectul unei fracții fără a-i schimba de fapt valoarea.
De exemplu, pot schimba 1/3 în fracția echivalentă 3/9 prin înmulțirea cu 3/3.
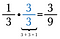
Să adunăm și să scădem părți de dimensiuni egale
Când adunăm și scădem fracții, numitorii trebuie să fie aceiași. Acest lucru are sens. Dacă dorim să combinăm sau să scădem părți trebuie să vorbim despre părți de aceeași mărime, altfel ar deveni confuz.
Atunci ce faci dacă fracțiile tale nu au aceleași mărimi?
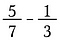
Înmulțiți cu o formă de unu pentru a schimba numitorii într-o mărime comună. În esență, împărțim fracțiile în bucăți de dimensiuni mai mici până când acestea au aceeași mărime. Acest lucru se numește găsirea unui numitor comun.
De fapt, orice numitor comun este suficient, dar oamenii preferă să-l găsească pe cel mai mic. În acest caz, cel mai mic număr în care intră atât 7 cât și 3 fără rest este 21. Deci, înmulțiți prima fracție cu 3/3 și a doua cu 7/7.
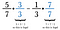
Dacă nu vă puteți gândi la cel mai mic numitor comun, puteți înmulți oricând fiecare fracție cu numitorul opus. Uneori, ca în acest caz, acesta se dovedește a fi cel mai mic numitor comun. Dacă nu este, doar reduceți răspunsul la sfârșit.
După ce numitorii se potrivesc, scădeți numărătorii pentru a obține 8/21.
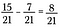
Acest lucru funcționează așa cum ne-am aștepta. Pictural, începeți cu 15 piese din 21 în total.

Îndepărtați coloritul de pe 7 din cele 15 blocuri albastre.

Ceea ce lasă 8/21 așa cum era de așteptat.
Schimbați mai întâi numerele mixte
Un număr mixt este combinația dintre un număr întreg și o fracție.
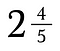
Numerele mixte nu se joacă bine cu alte fracții. Este o idee bună să le convertim mai întâi în fracții improprii.
Nota: O fracție improprie este o fracție al cărei numărător este mai mare decât numitorul său, având astfel o valoare mai mare decât unu.
Convertirea unui număr mixt este de fapt o adunare
Pentru a converti 2 și 4/5 într-o fracție improprie adăugați 2 + 4/5.
Pasul 1: Începeți prin a rescrie 2 ca 2/1.
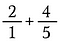
Pasul 2: Înmulțiți 2/1 cu 5/5 pentru a obține o fracție echivalentă de 10/5 care are numitorul comun dorit de 5.
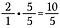
Etapa 3: Adăugați 10/5 + 4/5.
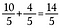
Rezultatul nostru este fracția improprie echivalentă 14/5.
Pentru a converti înapoi la un număr mixt efectuați împărțirea. De exemplu, 5 intră de două ori în 14 (deoarece 5 x 2 = 10), rămânând 4 bucăți.
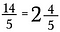
Comparați fracții folosind produsul încrucișat
Să presupunem că vrem să determinăm care este mai mare: 5/12 sau 6/13.
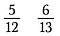
Primul pas: Înmulțiți o diagonală și scrieți produsul deasupra numărătorului.
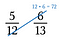
Pasul doi: Înmulțiți cealaltă diagonală și scrieți produsul acesteia deasupra numărătorului său.
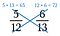
Pasul trei: Comparați produsele. Partea cu produsul cel mai mare este fracția cea mai mare. Deci, în acest caz, 5/12 este mai mic decât 6/13.
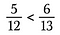
Potem determina dacă fracțiile sunt egale folosind și produsele încrucișate.
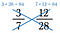
Produsul încrucișat al lui 3/7 și 12/28 sunt amândouă 84, prin urmare 3/7 = 12/28.
Anulați orice se împarte la unu
Cel mai bun lucru despre fracții este că puteți găsi o mulțime de oportunități de anulare. Ceea ce le face rapide și ușor de gestionat.
Supunem că am fracția 8/10. Atât 8 cât și 10 pot fi rescrise cu 2 ca factor.
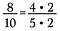
Pentru că 2/2 = 1, pot anula cei 2 lăsând 4/5 ca fracție redusă.
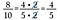
Utilizați această strategie pentru a face mai ușoară și înmulțirea fracțiilor.
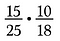
Începeți prin a rescrie fiecare număr în factori.
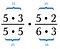
Anulați orice pereche de numere care se împart la 1. De exemplu, 5/5 = 1.
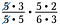
Am o altă pereche de 5, precum și o pereche de 3 care se împart tot la 1.
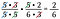
Oops! Aș fi putut rescrie 6 ca 2 x 3 și să anulez o pereche de 2. Este în regulă dacă vă scapă un factor, continuați până când le obțineți pe toate.
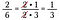
Dacă aș fi înmulțit direct 15/25 cu 10/18 ar fi fost multă aritmetică, folosind anularea pre-reduc fracțiile și fac mai simplă înmulțirea.
Utilizați înmulțirea pentru a împărți fracții
Conceptul de împărțire a fracțiilor este ușor cu exemple simple, cum ar fi:

Există două jumătăți într-un întreg, deci există 10 jumătăți în 5 întregi.
Dar conceptul devine dificil cu fracții mai complicate.
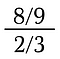
Pentru a rezolva această problemă vom utiliza două fapte:
- Potem înmulți cu orice formă de unu (i.adică orice peste el însuși)
- Multiplicând cu reciproca lui 3/2, care este 2/3, rezultă 1 prin anulare
Primul pas: Începeți prin a înmulți cu reciproca peste ea însăși.
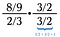
Acum avem de rezolvat două probleme mai mici (albastru și verde).
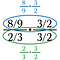
Pasul doi: Anulați tot ceea ce se împarte la 1 în fracția de jos (verde). Acest lucru ar trebui să rezulte întotdeauna în 1.

Acum ne rămâne de rezolvat problema de sus.
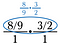
Pasul trei: Folosiți anularea pentru a pre-reduce fracția. După efectuarea acestor reduceri, înmulțiți transversal pentru a obține 4/3.

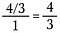
Shortcut
Aceasta este mecanica mâinii lungi a „întoarce și înmulțește”.”
Putem sări peste înmulțirea cu reciproca de jos, deoarece aceasta se anulează întotdeauna la 1. Prin urmare, tot ce trebuie să faceți este să înmulțiți numitorul cu reciproca numitorului.

Bonus: Teoria, în caz că vă interesează…
Bună întrebare! Pentru a generaliza, faceți două fracții folosind literele a, b, c și d pentru a reprezenta patru numere diferite.
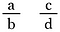
Multiplicați ambele fracții cu b-d (acest lucru ne va permite să anulăm numitorii).
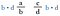
Acum anulăm b din stânga și d din dreapta, deoarece se împart la 1. Nu mai avem fracții, ci doar produsele d-a și c-b.
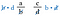
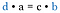
Vezi înapoi la fracțiile inițiale. Acestea sunt aceleași produse ca și cum am fi înmulțit diagonalele. Prin urmare, prescurtarea este să comparăm produsul încrucișat.
❤ RĂMÂNEȚI CONECTAT ❤
Stați la curent cu tot ce face Math Hacks!
.