Ecuațiile Lotka-Volterra descriu un model ecologic prădător-pradă (sau parazit-gazdă) care presupune că, pentru un set de constante pozitive fixe 
(rata de creștere a prăzii), 
(rata de distrugere a prăzii de către prădători), 
(rata de mortalitate a prădătorilor) și 
(rata de creștere a prădătorilor prin consumarea prăzii), se îndeplinesc următoarele condiții.
1. O populație de pradă 
crește cu o rată 
(proporțională cu numărul de prăzi), dar este simultan distrusă de prădători cu o rată 
(proporțională cu produsul dintre numărul de prăzi și numărul de prădători).
2. O populație de prădători 
scade cu o rată 
(proporțională cu numărul de prădători), dar crește cu o rată 
(din nou proporțională cu produsul dintre numărul de prăzi și numărul de prădători).
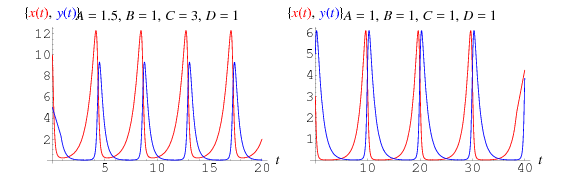
Aceasta dă ecuațiile diferențiale cuplate
 |
 |
 |
(1)
|
 |
 |
 |
(2)
|
soluțiile cărora sunt reprezentate grafic mai sus, în care prada este reprezentată în roșu, iar prădătorii în albastru. În acest tip de model, curba prăzii conduce întotdeauna curba prădătorilor.
Punctele critice apar atunci când 
, deci
 |
 |
 |
(3)
|
 |
 |
 |
(4)
|
Unicul punct staționar este așadar situat la 
.