Introducere
În această pagină se trece în revistă ecuația de continuitate, care impune conservarea masei într-o analiză euleriană. Aceasta nu este strict o descriere a comportamentului materialelor, dar ecuația rezultată este adesea folosită ca o identitate pentru a manipula algebric modelele constitutive care descriu comportamentul materialelor. Așadar, merită să fie analizată. Este, de asemenea, esențială pentru analiza curgerii fluidelor, deoarece analizele clasice ale fluidelor nu pot fi lagrangiane, deoarece pozițiile tuturor particulelor de fluid la \(t = 0\) sunt necunoscute.
Conservarea masei
Ecuația de continuitate reflectă faptul că masa se conservăîn orice analiză de mecanică a continuumului non-nucleară. Ecuația estedezvoltată prin însumarea vitezei cu care masa intră și iese dintr-un volum de control și prin stabilirea fluxului net de intrare egal cu rata de variație a masei în interiorul acestuia. Acest lucru este demonstrat în figura de mai jos.
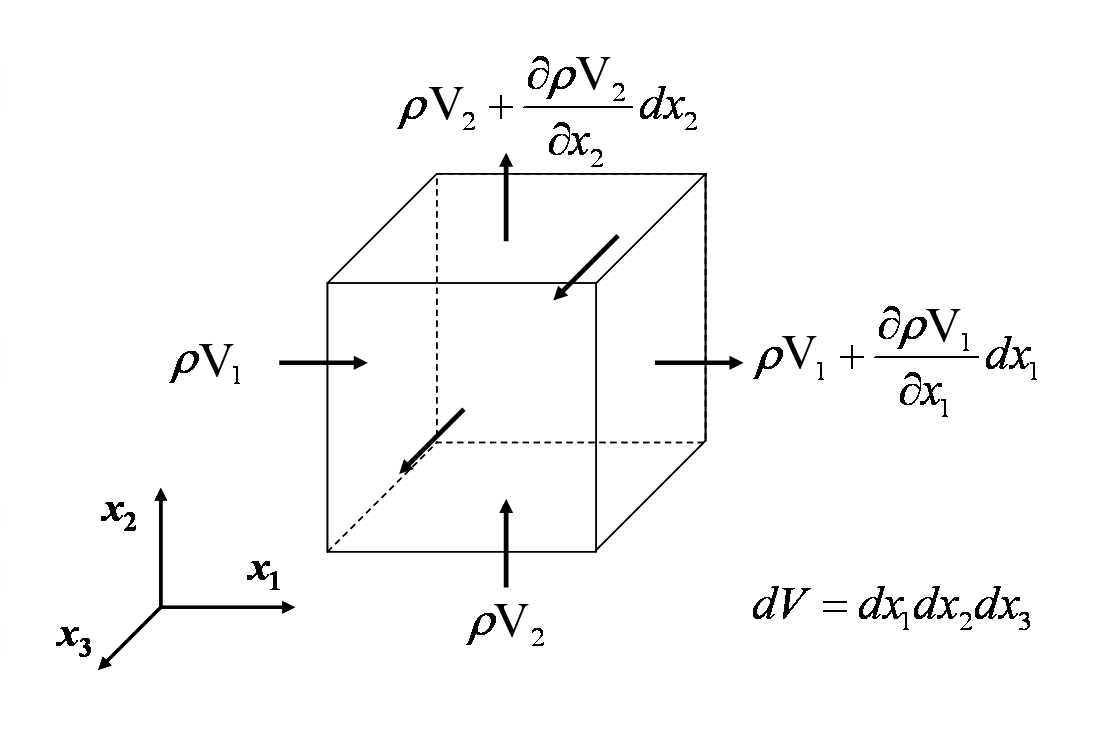
Să punem în ecuație toate debitele de masă care intră și ies din volumul de control diferențial rezultă
\
Cancelând termenii și împărțind prin \(dx_1 dx_2 dx_3\) rezultă
\
și rearanjând se obține
\
Acest lucru poate fi scris concis sub forma
\

Puncturi importante
Acestea sunt cele finale, complete și cele mai generale forme ale ecuației de continuitate care impune conservarea masei. Ea se aplică tuturor materialelor,nu doar fluidelor. Deci se aplică și la solide. Rețineți că este o singură ecuație scalară și că este de natură euleriană, deoarece termenii gradientului sunt \({\partial \ peste \partial x_i}\), nu \({\partial \ peste \partial X_i}\).
Se poate pune întrebarea dacă există un corespondent lagrangian la forma euleriană a acestei ecuații. Există. Aceasta se scrie de obicei sub forma
\
Aceasta afirmă pur și simplu că bucățica diferențială a masei în starea deformată\(\rho \, dV\) trebuie să fie egală cu valoarea sa inițială\(\rho_o dV_o\) în starea nedeformată.
Există mai multe cazuri speciale ale ecuației de continuitate.Primul apare atunci când curgerea este în regim staționar. În acest caz, derivata în raport cu timpul este zero, rămânând.
\
Cel de-al doilea caz special este cel al incompresibilității, adică, \(\rho = \)constantă.În acest caz, derivata în raport cu timpul este zero și \(\rho\) poate fi eliminată din ecuație, rămânând doar
\
Acest rezultat este suficient de simplu pentru a fi adesea extins.
\\
Rețineți că acest lucru nu este nimic mai mult decât \(\text{tr}({\bf D}) = 0\) pentru cazul materialelor incompresibile.

Derivată de material
Ceea ce urmează merită să fie subliniată deoarece permite separarea vectorului densitate și viteză. Primul pas este să aplicăm regula produsului la termenul de divergență din ecuația de continuitate.
\
Și apoi să observăm că\({\partial \rho \ peste \partial t} + {\bf v} \cdot \nabla \rho\)este doar derivata materială a densității,\({D \rho \ peste D t}\).
Deci ecuația de continuitate poate fi, de asemenea, scrisă ca
\
Dacă materialul este incompresibil, atunci \(\rho\) nu se poate modifica, deci \( {D \rho \ peste D t} \) trebuie să fie zero, lăsând
\
Și apoi se împarte prin \(\rho\) (deoarece nu este zero) pentru a obține
\

Ecuația de continuitate Exemplu
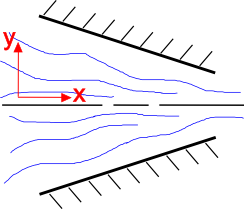
Este intuitiv faptul că curgerea fluidului se accelerează pe măsură ce suprafața secțiunii transversale scade, așa cum se arată în dreapta. Ecuația de continuitate explică acest lucru. Luați în considerare un câmp de curgere 2-D, în stare staționară, a unui fluid incompresibil.Ecuația de continuitate pentru această situație este
\
Începeți prin a privi componenta y a curgerii, \(v_2\). Geometria duzei convergente forțează componenta \(v_2\) să curgă în sus când \(y \lt 0\) și să curgă în jos când \(y \gt 0\). Deci \(v_2 \gt 0\) când \(y \lt 0\) și \(v_2 \lt 0\) când \(y \gt 0\).
Efectul net al acestui lucru este că \({\partial v_2 \ peste \partial x_2} \lt 0\)în duza convergentă.
Dar ecuația de continuitate dictează că suma celor două derivate parțiale trebuie să fie egală cu zero. Deci, dacă a doua este mai mică decât zero, atunci
\
Și asta înseamnă că fluxul de fluid trebuie să fie în accelerare.
.