Cum să-i ajutăm pe elevii care se luptă cu problemele de cuvinte

„Ei cunosc matematica. Pur și simplu nu pot face problemele de cuvinte. Este vorba de înțelegerea lor de lectură.”

Doamna Hartwell explica de ce elevii ei au avut dificultăți la testele de stat. Ea își cunoștea elevii și făcuse evaluări ample. Era sigură că dificultățile lor erau o problemă de alfabetizare.

„Nu înțeleg de ce fac cititul atât de greu. Copiii dau deja un test de limbă și literatură.”

Fusesem asociat cu doamna Hartwell (și cu alții din școala ei) ca parte a unui program al orașului New York pentru a stimula rezultatele la matematică. Scopul era de a aduce matematica conceptuală în școlile „Tier 1”. Școlile de nivel 1 erau cele care conduceau orașul în trei domenii. Cele mai mici venituri, cele mai mici rezultate la teste și cel mai mare procent de elevi de culoare.

Am auzit explicația „alfabetizării” de la alți profesori din program. Și avea sens. Dacă elevii cunoșteau matematica, de ce altfel se chinuiau la test, care avea o mulțime de probleme de cuvinte?

Dar exista o capcană. În ultimii trei ani, competențele de alfabetizare au trecut de la 30%-40%, la nivelul întregului oraș. În aceeași perioadă, scorurile la matematică rămăseseră în mare parte neschimbate.

Dacă aceasta ar fi fost o problemă de citire, creșterile scorurilor la citire ar trebui să deblocheze o creștere explozivă la matematică. În plus, limbajul din problemele de cuvinte pur și simplu nu părea suficient de complicat pentru a cauza probleme.

În următoarea perioadă, am fost programat să vizitez clasa doamnei Hartwell. Ea planificase o lecție pe probleme de cuvinte, astfel încât să pot vedea problema la fața locului.

Supra-încadrarea problemelor de cuvinte

Elevii stăteau la mese rotunde, iar ea stătea în față. Ea și elevii ei aveau cu toții tablă albă de mână.

Au deschis manualele la pagina 47 și ea a citit cu voce tare o problemă de cuvinte. „Sarah are 40 de kg de morcovi pentru caii ei. Dacă ea are 100 de cai, câte kilograme primește fiecare cal?”

„OK, clasă, ea are 40 de livre pe care le va da fiecărui cal. Deci de ce operațiune avem nevoie?”

A arătat spre o diagramă de ancorare care enumeră „cuvintele cheie” pentru fiecare operație. ‘Fiecare’ era în capul listei de diviziune.

„Diviziune!” a răspuns clasa.

„Corect. Deci cum împărțim un număr mic la un număr mare?”

Clasa a rămas tăcută. Doamna Hartwell a desenat un vinculum (casa diviziunii lungi) pe tablă. Elevii au copiat în timp ce ea a pus 40 sub casă și 100 afară.

„Acum 100 nu încape în 40, așa că trebuie să adăugăm o zecimală.” Ea a schimbat 40 în 40,0. „De câte ori intră 100 în 400?”.

Câțiva elevi au strigat „Patru!”.

„Exact. Acum, trebuie să punem o zecimală și în cutientul nostru. Răspunsul nostru final este?”

Clasa a citit răspunsul, „0,4”, de pe tablă.

A repartizat o problemă similară și a arătat spre posterul „CUBE” de pe perete. „Nu uitați să încercuiți numerele și să încadrați cuvintele cheie.”

Ea a circulat în timp ce elevii lucrau. Unii au întrebat unde să pună zecimalele. Alții au avut probleme în a alinia partea de scădere a împărțirii lungi. Unii elevi au lucrat în perechi, unul dintre ei făcând calculele, în timp ce celălalt copia.

Până la sfârșitul lecției, toată lumea avea răspunsul corect pe hârtie. „Vedeți?” a remarcat doamna Hartwell, „toți știu matematica.”

Ce a mers prost?

În timp ce acesta este un exemplu extrem, multe dintre greșelile pe care le-a făcut doamna Hartwell sunt de fapt destul de comune.

Supra-învățarea apare atunci când le oferim elevilor prea mult sprijin. În timp ce este obișnuit ca educatorii să se mândrească cu faptul că le oferă elevilor „atât de mult sprijin cât au nevoie”, supra-ajustarea este diferită.

Termenul „scaffolding” provine din munca lui Lev Vygotsky. El a inventat termenul „Zona de dezvoltare proximală”. ZPD include lucruri care se află chiar în afara razei de acțiune a celui care învață. Aceștia nu le pot face pe cont propriu, dar le pot face cu sprijin. Prin „eșafodaj”, putem muta aceste abilități în setul de abilități de bază al unui cursant.

Ceea ce este adesea trecut cu vederea este că eșafodajul se aplică numai la abilitățile care se află deja în ZPD a unui cursant. Există o gamă întreagă de competențe care, în prezent, nu sunt la îndemâna unui cursant. Atunci când încercăm să schelărim aceste abilități, facem mai mult rău decât bine.

O problemă a schelării excesive este că elevii nu internalizează niciodată abilitățile vizate. Atunci când ajutăm un elev cu ceva în afara ZPD-ului său, acesta va avea întotdeauna nevoie de ajutorul nostru. Cel puțin până când identificăm abilitățile intermediare care se află în ZPD-ul lor.

O altă problemă este că supra-învățarea ne dă un fals sentiment de succes. În acest caz, doamna Hartwell a crezut că elevii ei puteau „face calculele matematice” din problema de cuvinte. În realitate, ei nu făceau decât să imite acțiunile ei. Nu exista niciun motiv pentru a crede că ar fi putut găsi o soluție similară pe cont propriu.

De asemenea, ea a eliminat întregul proces de ‘formulare’ din procesul de rezolvare a problemelor. Mulți educatori consideră că înțelegerea și formularea sunt același lucru, dar formularea este o competență matematică separată.

Și s-ar putea să fie ingredientul care lipsește din modul în care predați în prezent problemele de cuvinte.

Classroom Resources and Professional Learning

Formulare: Cheia succesului în rezolvarea problemelor de cuvinte

Formularea problemelor de cuvinte presupune înțelegerea acestora. Dar merge dincolo de aceasta. Formularea seamănă mai mult cu traducerea decât cu înțelegerea.

Când un elev citește o problemă de cuvinte, mai întâi, trebuie să transforme literele în sunete (decodificare). Apoi, ei trebuie să înțeleagă ce înseamnă cuvintele (vocabular). Ei trebuie să înțeleagă cum se potrivesc cuvintele într-o propoziție (sintaxă). În cele din urmă, înțelegerea vine din punerea acestor piese împreună pentru a da sens.

Majoritatea elevilor de clasa a VI-a ar putea citi problema doamnei Hartwell și ar înțelege cu ușurință că Sarah împarte morcovi cailor ei. Dar mult mai puțini vor face legătura între „împărțirea” morcovilor și diviziune.

Aceasta este partea care îi încurcă pe mulți educatori. Nouă ni se pare atât de evidentă. „Ea împarte literalmente morcovii. Cum să nu vadă că este vorba de împărțire?”.

Ei pur și simplu nu văd. Dacă ar face-o, nu ați vedea diagrame cu cuvinte cheie atârnate în clasele de matematică. Și totul se întoarce la momentul în care predăm pentru prima dată operațiile.

De ce se luptă elevii cu formularea

Mulți profesori din multe școli îi învață pe elevi că matematica este o materie de formulare a sensurilor. Dar în altele, matematica este predată ca o materie de memorare.

Un exemplu de „matematică ca amintire” este atunci când elevii memorează date matematice. Dar algoritmii sunt, de asemenea, despre memorare. Puneți 120 peste 47. Urmați acești pași pentru a aduna, aceștia pentru a scădea scăderea și aceștia pentru a înmulți.

Elevii pot repeta acești pași fără să înțeleagă mărimea numerelor sau chiar ce înseamnă operațiile.

Când începem cu concepte (folosind modele vizuale sau propoziții numerice), elevii învață ce înseamnă operațiile. Când trecem direct la un algoritm, elevii se gândesc la operații ca la o serie de pași aleatorii.

An după an, îi punem pe elevi să rețină și să repete. Ei completează același algoritm de 30 de ori pentru temele pentru acasă. Schimbați numerele, iar procesul rămâne același. Dar dați-le o problemă de cuvinte, iar acum trebuie să le dea un sens.

Ce ne spun testele despre raționament

Am putea să le dăm elevilor noștri 10 probleme cu titlul „Probleme de cuvinte de împărțire”, pentru a le face mai ușor. Ei nici măcar nu vor avea nevoie să citească problemele. Ei trebuie doar să își dea seama (sau să ghicească) care număr este divizorul și care este dividendul.

Dar atunci când elevii se prezintă la un test de stat, scopul nu este de a-l face mai ușor. Scopul este de a evalua ceea ce pot face pe cont propriu.

Creatorii de teste nu vor să le spună ce operație să folosească. Ei vor pune chiar și cuvinte cheie pentru împărțire și adunare în aceeași problemă. „Sunt 20 de elevi în clasă. Dacă fiecare copil are trei dolari, cât au în total?”.

Deci, atunci când elevii se luptă cu problemele de cuvinte, nu este vorba doar de problemele de cuvinte. De obicei, înseamnă că ei fac matematică din memorie. Trebuie să-i învățăm că matematica se referă la crearea de sensuri.

Elevii au nevoie de strategii și procese pentru a rezolva probleme de cuvinte

O parte a problemei cu un sistem precum CUBES este că se numește pe sine o strategie, dar este de fapt un proces.

Un proces este o serie de pași. Odată ce identificați un proces eficient, îl puteți repeta din nou și din nou fără să vă gândiți prea mult. Algoritmii sunt un proces. La fel ca și alinierea „de la cel mai înalt la cel mai scund” pentru mersul pe jos spre prânz.

O strategie este diferită. Strategiile necesită o înțelegere profundă. Și capacitatea de a aplica înțelegerea în situații noi.

Nu putem pregăti elevii pentru fiecare scenariu pe care îl vor întâlni într-o problemă de cuvinte. Unele necesită ca ei să combine diferite abilități matematice pe care nu le-au combinat niciodată înainte. Sau pot necesita ca elevii să schimbe ordinea pașilor pentru a ajunge la soluția corectă.

Considerați următoarele:

Aveți 5 galoane de suc pentru un eveniment școlar cu 100 de elevi. Dacă fiecare pahar conține 3 oz, câte pahare poate bea fiecare elev? Cât va rămâne.

Un proces de rezolvare a problemelor îi poate ajuta pe elevi să înceapă să abordeze această problemă. „Identificați ceea ce se cere”. „Luați în considerare ce informații sunt date.”

Dar nu există un proces prestabilit pe care să îi învățăm să o rezolve efectiv. Aici intervine strategia. Ei trebuie să convertească unitățile. Să recunoască faptul că împărțim cu resturi, mai degrabă decât să împărțim complet. De asemenea, probabil că ar trebui să reordoneze operațiile, împărțind sucul în pahare înainte de a împărți la numărul de elevi.

Nu există niciun „truc” care să îi ducă pe elevi acolo. Ei trebuie să înțeleagă semnificația operațiilor. Ei trebuie să înțeleagă matematica ca pe un subiect de creare de sensuri. Și au nevoie să exerseze în mod repetat aplicarea gândirii strategice la problemele de tip word.

Procesul Polya pentru rezolvarea problemelor de tip word

George Pólya a fost un influent matematician maghiar și profesor la Stanford care a găsit un proces care poate fi folosit pentru a rezolva orice problemă. Munca sa a atins nenumărați matematicieni și educatori, dintre care cei mai mulți nu-i cunosc numele.

De fapt, CUBES și alte așa-numite strategii de rezolvare a problemelor se bazează vag pe munca sa. Problema este că ele încearcă să o simplifice. În acest proces, ele elimină tot ceea ce seamănă cu o gândire profundă.

Polya credea că orice problemă poate fi rezolvată în patru pași: Înțelege, Planifică, Rezolvă și Reflectează. Cred că procesul original în patru pași al lui Polya este foarte bun pentru a fi folosit în școli.

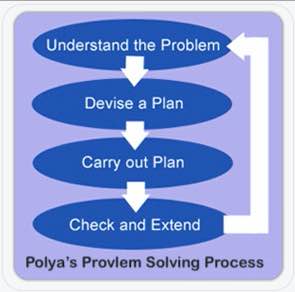Pentru a înțelege problema, identificăm ce informații sunt date și ce vrem să găsim. De aici vin „C” și „U” din cuburi. Dacă elevii vor să încercuiască numerele și să sublinieze întrebarea, foarte bine. Eu prefer ca ei să le scrie (cu unitățile) într-un organizator grafic, cel puțin la început. Acest lucru îi ajută să proceseze ceea ce citesc. De asemenea, mă ajută și pe mine, în calitate de profesor, să le evaluez înțelegerea în timp ce mă plimb prin sală.

În continuare este partea dificilă. „Planul” este locul în care formulăm problema. Luăm un scenariu din lumea reală și îl transformăm într-o altă reprezentare matematică.

Al treilea pas este să rezolvăm. Dacă am formulat corect, aici este momentul în care calculăm. Elevii folosesc de obicei un algoritm, dar încurajez utilizarea ecuațiilor și a modelelor vizuale, de asemenea.

În cele din urmă, elevii se uită înapoi și își verifică munca. Ei ar trebui, de asemenea, să reflecteze asupra procesului lor. Dacă am făcut o greșeală, de ce? Ar putea această strategie să mă ajute să rezolv probleme similare în viitor?

Strategii pentru rezolvarea problemelor de cuvinte

Având un proces de abordare a problemelor de cuvinte este cu siguranță util. Dar nu putem pretinde că matematica semnificativă se învață doar urmând niște pași. Întregul scop al problemelor de cuvinte este de a extinde matematica dincolo de „fapte matematice” și algoritmi.

Există câteva strategii utile pentru a-i ajuta pe elevi cu formularea. La început, predau în mod explicit o serie de strategii diferite.

În timp ce predau strategiile, îi pun pe elevi să rezolve probleme care se potrivesc bine cu strategia respectivă. Unele tipuri de probleme se potrivesc foarte bine cu ‘Ghicește și verifică’. Altele sunt mai potrivite pentru ‘Desenează o imagine’.

În cele din urmă, le dau probleme de cuvinte provocatoare care pot fi rezolvate în mai multe moduri. Odată ce au instrumentele în centura de instrumente, ei pot alege care este cea mai bună pentru situația respectivă.

Combinarea strategiilor poate fi, de asemenea, foarte eficientă. De exemplu, desenarea unei imagini poate fi adesea utilă pentru a ajuta la formulare. Dacă un fermier are 18 rânduri de morcovi și 10 morcovi în fiecare rând, un elev poate începe prin a desena câmpul. La un moment dat, ei se pot gândi „Wow, aceasta este o matrice” și își dau seama că pot înmulți folosind matematica mentală, o expresie sau un algoritm.

Alteori, elevii pot folosi modele vizuale pentru a formula și a rezolva problema.

Ajutați-i pe elevii dvs. să abordeze probleme de cuvinte dificile

Dacă sunteți ca mulți profesori, s-ar putea să fiți îngrijorat de modul în care elevii dvs. vor face față la toate acestea. Procese, strategii, gândire critică… sunt multe lucruri implicate.

S-ar putea chiar să vă gândiți că problemele de cuvinte păreau mai ușoare înainte de acest articol. Dacă este așa, îmi cer scuze.

Cheia este să nu vă simțiți copleșiți încercând să faceți totul deodată. Începeți prin a rezolva o problemă simplă de cuvinte folosind procesul lui Polya. Apoi, introduceți o nouă strategie în fiecare săptămână. Până la sfârșitul anului, veți fi uimit de cât de departe au ajuns.

Poate că sunteți interesat să aprofundați rezolvarea creativă a problemelor. Luați în considerare participarea la un atelier practic de matematică sau colaborarea cu un antrenor online.

Dacă sunteți gata să aduceți mâine un pic de Polya în clasa dumneavoastră, acest organizator grafic este o modalitate excelentă de a începe. Acesta va schelda procesul în patru pași și vă va ajuta să identificați unde elevii dvs. se abat de la drumul cel bun.

Organizator gratuit de probleme de cuvinte

Despre autor

Jeff Lisciandrello este fondatorul Room to Discover și un consultant în educație specializat în învățarea centrată pe elev. Designul său de 3 poduri pentru învățare ajută școlile să exploreze practici inovatoare în cadrul mediilor tradiționale. Îi place să îi ajute pe educatori să adopte abordări bazate pe anchetă și abordări personalizate ale instruirii. Puteți lua legătura cu el prin Twitter @EdTechJeff

.