Algoritmul Toom-Cook
Învățăm aici o aplicație ingenioasă a unui algoritm de împărțire și cucerire combinat cu algebra liniară pentru a înmulți numere mari, rapid. Și o introducere în notația big-O!
De fapt, acest rezultat este atât de contra-intuitiv încât marele matematician Kolmogorov a conchis că un algoritm atât de rapid nu există.
Partea 0: Înmulțirea lungă este o înmulțire lentă. (Și o introducere în notarea Big-O)
Cu toții ne amintim că am învățat să înmulțim la școală. De fapt, eu am o mărturisire de făcut. Țineți minte, aceasta este o zonă fără judecată 😉
La școală, aveam „joaca umedă” atunci când ploua prea tare pentru a ne juca în terenul de joacă. În timp ce ceilalți copii (normali / iubitori de distracție / cu adjectiv pozitiv de alegere) se jucau și își făceau de cap, eu luam uneori o foaie de hârtie și înmulțeam numere mari împreună, doar de dragul de a o face. Bucuria pură a calculului! Aveam chiar și o competiție de înmulțire, „Super 144”, în care trebuia să înmulțim o grilă de numere de 12 pe 12 amestecate (de la 1 la 12) cât mai repede posibil. Am exersat acest lucru cu religiozitate, până într-acolo încât aveam propriile mele foi de exerciții pregătite în prealabil, pe care le fotocopiam și apoi le foloseam prin rotație. În cele din urmă am reușit să reduc timpul la 2 minute și 1 secundă, moment în care mi-a fost atinsă limita fizică de mâzgălit.
În ciuda acestei obsesii pentru înmulțire, nu m-am gândit niciodată că am putea să o facem mai bine. Am petrecut atâtea ore înmulțind, dar nu am încercat niciodată să îmbunătățesc algoritmul.
Considerați înmulțirea lui 103 cu 222.
Calculăm 2 ori 3 ori 1 +2 ori 0 ori 10 + 2 ori 1 ori 100 + 20 ori 3 ori 1 + 20 ori 0 ori 10 + 20 ori 1 ori 100 = 22800
În general, pentru a înmulți la numere de n cifre, este nevoie de O(n²) operații. Notația „big-O” înseamnă că, dacă ar fi să reprezentăm grafic numărul de operații în funcție de n, termenul n² este cel care contează cu adevărat. Forma este în esență pătratică.
Astăzi ne vom îndeplini toate visele din copilărie și vom îmbunătăți acest algoritm. Dar mai întâi! Big-O ne așteaptă.
Big-O
Vezi cele două grafice de mai jos

Întrebați un matematician, „sunt x² și x²+x^(1/3) la fel?”, și probabil că va vomita în ceașca de cafea și va începe să plângă, și va mormăi ceva despre topologie. Cel puțin, aceasta a fost reacția mea (la început), și eu abia dacă știu ceva despre topologie.
Ok. Nu sunt același lucru. Dar computerului nostru nu-i pasă de topologie. Computerele diferă în ceea ce privește performanța în atât de multe moduri pe care nici măcar nu le pot descrie pentru că nu știu nimic despre computere.
Dar nu are rost să reglăm fin un rulou cu abur. Dacă două funcții, pentru valori mari ale intrării lor, cresc cu același ordin de mărime, atunci, în scopuri practice, acest lucru conține cea mai mare parte a informațiilor relevante.
În graficul de mai sus, vedem că cele două funcții arată destul de asemănător pentru intrări mari. Dar, la fel, x² și 2x² sunt similare – cea din urmă este doar de două ori mai mare decât prima. La x = 100, una este de 10.000 și cealaltă de 20.000. Asta înseamnă că dacă putem calcula una, probabil că o putem calcula și pe cealaltă. În timp ce o funcție care crește exponențial, să zicem 10^x, la x = 100 este deja mult mai mare decât numărul de atomi din univers. (10¹⁰⁰ >>>>> 10⁸⁰ care este o estimare, numărul Eddington, privind numărul de atomi din univers, conform căutării mele pe Google*).
*de fapt, am folosit DuckDuckGo.
Scrierea numerelor întregi sub formă de polinoame este atât foarte naturală, cât și foarte nefirească. A scrie 1342 = 1000 + 300 + 40 + 2 este foarte natural. A scrie 1342 = x³+3x²+4x + 2, unde x = 10, este ușor ciudat.
În general, să presupunem că vrem să înmulțim două numere mari, scrise în baza b, cu n cifre fiecare. Scriem fiecare număr cu n cifre sub forma unui polinom. Dacă împărțim numărul de n cifre în r bucăți, acest polinom are n/r termeni.
De exemplu, fie b = 10, r = 3, iar numărul nostru este 142,122,912
Potem transforma acest lucru în
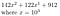
Acest lucru funcționează foarte bine atunci când r = 3 și numărul nostru, scris în baza 10, avea 9 cifre. Dacă r nu împarte perfect n, atunci putem adăuga doar câteva zerouri în față. Din nou, acest lucru este cel mai bine ilustrat de un exemplu.
27134 = 27134 + 0*10⁵ = 027134, pe care îl reprezentăm ca
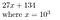
De ce ar putea fi util acest lucru? Pentru a afla coeficienții polinomului P, dacă polinomul este de ordinul N, atunci prin eșantionarea lui în N+1 puncte putem determina coeficienții săi.
De exemplu, dacă polinomul x⁵ + 3x³ +4x-2, care este de ordinul 5, este eșantionat în 6 puncte, putem apoi să calculăm întregul polinom.
Intuitiv, un polinom de ordin 5 are 6 coeficienți: coeficientul lui 1, x, x, x², x³, x⁴, x⁵. Având 6 valori și 6 necunoscute, putem afla valorile.
(Dacă știți algebră liniară, puteți trata diferitele puteri ale lui x ca vectori liniar independenți, puteți face o matrice pentru a reprezenta informația, inversați matricea și iată)
Eșantionarea polinoamelor pentru a determina coeficienții (opțional)
Aici analizăm puțin mai în profunzime logica care stă la baza eșantionării unui polinom pentru a deduce coeficienții săi. Nu ezitați să treceți la secțiunea următoare.
Ceea ce vom arăta este că, dacă două polinoame de grad N sunt de acord în N+1 puncte, atunci ele trebuie să fie identice. Adică N+1 puncte specifică în mod unic un polinom de ordinul N.
Considerăm un polinom de ordinul 2. Acesta este de forma P(z) = az² +bz + c. Prin teorema fundamentală a algebrei – fără rușine, conectați-vă aici, am petrecut câteva luni de zile pentru a pune cap la cap o demonstrație în acest sens și apoi am scris-o, aici – acest polinom poate fi factorizat. Asta înseamnă că îl putem scrie ca A(z-r)(z-w)
Rețineți că la z = r, și la z = w, polinomul se evaluează la 0. Spunem că w și r sunt rădăcini ale polinomului.
Acum vom arăta că P(z) nu poate avea mai mult de două rădăcini. Să presupunem că are trei rădăcini, pe care le numim w, r, s. Apoi factorizăm polinomul. P(z) = A(z-r)(z-w). Atunci P(s) = A(s-r)(s-w). Acesta nu este egal cu 0, deoarece înmulțirea numerelor care nu sunt zero dă un număr care nu este zero. Aceasta este o contradicție deoarece ipoteza noastră inițială a fost că s este o rădăcină a polinomului P.
Acest argument poate fi aplicat unui polinom de ordin N într-un mod esențial identic.
Acum, să presupunem că două polinoame P și Q de ordin N sunt în acord în N+1 puncte. Atunci, dacă ele sunt diferite, P-Q este un polinom de ordin N care este 0 în N+1 puncte. Prin cele anterioare, acest lucru este imposibil, deoarece un polinom de ordin N are cel mult N rădăcini. Așadar, presupunerea noastră trebuie să fi fost greșită, iar dacă P și Q sunt de acord în N+1 puncte, ele sunt același polinom.
Să vezi înseamnă să crezi: A Worked Example
Să ne uităm la un număr foarte mare pe care îl numim p. În baza 10, p are 24 de cifre (n=24) și îl vom împărți în 4 bucăți (r=4). n/r = 24/4 = 6
p = 292,103,243,859,143,157,364,152.
Și fie ca polinomul care îl reprezintă să se numească P,
P(x) = 292,103 x³ + 243,859 x² +143,157 x+ 364,152
cu P(10⁶) = p.
Cum gradul acestui polinom este 3, putem calcula toți coeficienții din eșantionarea în 4 locuri. Să ne facem o idee despre ce se întâmplă când îl eșantionăm în câteva puncte.
- P(0) = 364,152
- P(1) = 1,043,271
- P(-1) = 172,751
- P(2) = 3,962,726
Un lucru izbitor este că toate acestea au 6 sau 7 cifre. Asta în comparație cu cele 24 de cifre găsite inițial în p.
Să înmulțim p cu q. Fie q = 124,153,913,241,143,634,899,130 și
Q(x) = 124,153 x³ + 913,241 x²+143,634 x + 899,130
Calcularea t=pq ar putea fi oribilă. Dar în loc să o facem direct, încercăm să calculăm reprezentarea polinomială a lui t, pe care o etichetăm T. Cum P este un polinom de ordinul r-1=3, iar Q este un polinom de ordinul r-1 = 3, T este un polinom de ordinul 2r-2 = 6.
T(10⁶) = t = pq
T(10⁶) = P(10⁶)Q(10⁶)
Trucul constă în faptul că vom calcula coeficienții lui T, în loc să înmulțim direct p și q împreună. Apoi, calcularea lui T(1⁰⁶) este ușoară, deoarece pentru a înmulți cu 1⁰⁶ nu trebuie decât să lipim 6 zerouri în spate. Însumarea tuturor părților este, de asemenea, ușoară, deoarece adunarea este o acțiune foarte puțin costisitoare pentru calculatoare.
Pentru a calcula coeficienții lui T, trebuie să îl eșantionăm în 2r-1 = 7 puncte, deoarece este un polinom de ordinul 6. Probabil că dorim să alegem numere întregi mici, așa că alegem
- T(0)=P(0)Q(0)= 364,152*899,130
- T(1)=P(1)Q(1)= 1,043,271*2,080,158
- T(2)=P(2)Q(2)= 3,962,726*5,832,586
- T(-1)=P(-1)Q(-1)= 172751*1544584
- T(-2)=P(-2)Q(-2)= -1,283,550*3,271,602
- T(3)=P(-3)Q(-3)= -5,757,369*5,335,266
Rețineți mărimea lui P(-3), Q(-3), P(2), Q(2) etc… Toate acestea sunt numere cu aproximativ n/r = 24/4 = 6 cifre. Unele sunt de 6 cifre, altele de 7 cifre. Pe măsură ce n devine mai mare, această aproximare devine din ce în ce mai rezonabilă.
Până acum am redus problema la următorii pași, sau algoritm:
(1) Mai întâi calculați P(0), Q(0), P(1), Q(1), etc. (acțiune cu costuri reduse)
(2) Pentru a obține cele 2r-1= 7 valori ale lui T(x), trebuie acum să înmulțim 2r-1 numere de dimensiuni aproximative de n/r cifre. Și anume, trebuie să calculăm P(0)Q(0), P(1)Q(1), P(-1)Q(-1), etc. (Acțiune cu costuri ridicate)
(3) Reconstruiți T(x) din punctele noastre de date. (Acțiune cu costuri reduse: dar va fi luată în considerare mai târziu).
(4) Cu T(x) reconstruit de noi, evaluați T(10⁶) în acest caz
Acest lucru duce frumos la o analiză a timpului de execuție al acestei abordări.
Timp de execuție
Din cele de mai sus, am aflat că, ignorând temporar acțiunile cu costuri reduse (1) și (3), costul înmulțirii a două numere de n cifre cu algoritmul lui Toom va respecta:
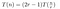
Acest lucru este ceea ce am văzut în exemplul lucrat. Înmulțirea fiecărui P(0)Q(0), P(1)Q(1), etc. costă T(n/r), deoarece înmulțim două numere de lungime aproximativ n/r. Trebuie să facem acest lucru de 2r-1 ori, deoarece dorim să eșantionăm T(x) – fiind un polinom de ordin 2r-2 – în 2r-1 locuri.
Cât de rapid este acest lucru? Putem rezolva acest tip de ecuație în mod explicit.

Tot ce mai rămâne acum este o oarecare algebră dezordonată
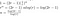
Ca urmare a altor costuri generate de procesul de înmulțire a matricei („reasamblare”), și din adunare, nu putem spune cu adevărat că soluția noastră este timpul de execuție exact, așa că, în schimb, concluzionăm că am găsit big-O al timpului de execuție
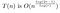
Optimizarea lui r
Acest timp de execuție depinde încă de r. Corectați r și am terminat. Dar curiozitatea noastră nu este încă satisfăcută!
Cum n devine mai mare, dorim să găsim o valoare aproximativ optimă pentru alegerea lui r. Adică dorim să alegem o valoare a lui r care să se modifice pentru diferite valori ale lui n.
Ceea ce este esențial aici este că, în cazul în care r variază, trebuie să acordăm o anumită atenție costului de reasamblare – matricea care efectuează această operație are un cost de O(r²). Când r era fix, nu trebuia să ne uităm la acest aspect, deoarece, pe măsură ce n creștea cu r fix, termenii care implicau n erau cei care determinau creșterea cantității de calcul necesare. Deoarece alegerea noastră optimă a lui r va crește pe măsură ce n crește, nu mai putem ignora acest lucru.
Această distincție este crucială. Inițial, analiza noastră a ales o valoare a lui r, poate 3, poate 3 miliarde, și apoi a analizat dimensiunea big-O pe măsură ce n creștea arbitrar de mare. Acum, ne uităm la comportamentul pe măsură ce n crește arbitrar de mare și r crește cu n cu o anumită rată pe care o stabilim. Această schimbare de perspectivă privește O(r²) ca pe o variabilă, în timp ce atunci când r era menținut fix, O(r²) era o constantă, deși una pe care nu o cunoșteam.
Acum, actualizăm analiza noastră de dinainte:
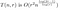
unde O(r²) reprezintă costul matricei de reasamblare. Acum dorim să alegem o valoare a lui r pentru fiecare valoare a lui n, care minimizează aproximativ această expresie. Pentru a minimiza, încercăm mai întâi să diferențiem în raport cu r. Acest lucru dă expresia cu aspect oarecum hidos

În mod normal, pentru a găsi punctul minim, se stabilește derivata egală cu 0. Dar această expresie nu are un minim frumos. În schimb, găsim o soluție „suficient de bună”. Folosim r = r^(sqrt(logN)) ca valoare estimativă. Din punct de vedere grafic, aceasta este destul de aproape de minim. (În diagrama de mai jos, factorul 1/1000 este acolo pentru a face graficul vizibil la o scară rezonabilă)
Graficul de mai jos arată funcția noastră pentru T(N), scalată cu o constantă, în roșu. Linia verde este la x = 2^sqrt(logN), care a fost valoarea noastră estimativă. ‘x’ ia locul lui ‘r’, iar în fiecare dintre cele trei imagini se folosește o valoare diferită a lui N.



Acest lucru este destul de convingător pentru mine că alegerea noastră a fost una bună. Cu această alegere a lui r, putem să o introducem și să vedem cum arată big-O-ul final al algoritmului nostru:

unde am introdus pur și simplu valoarea noastră pentru r și am folosit o aproximare pentru log(2r-1)/log(r) care este foarte precisă pentru valori mari ale lui r.
Cât de mare este îmbunătățirea?
Pe cât de mare este îmbunătățirea?
Poate că faptul că nu am observat acest algoritm când eram mic copil și făceam înmulțiri a fost rezonabil. În graficul de mai jos, dau coeficientul funcției noastre big-O să fie 10 (în scop demonstrativ) și îl împart cu x² (deoarece abordarea originală a înmulțirii era O(n²). Dacă linia roșie tinde spre 0, asta ar arăta că noul nostru timp de execuție se descurcă asimptotic mai bine decât O(n²).
Și, într-adevăr, deși forma funcției arată că abordarea noastră este în cele din urmă mai rapidă, și în cele din urmă este mult mai rapidă, trebuie să așteptăm până când vom avea numere lungi de aproape 400 de cifre pentru ca acest lucru să fie cazul! Chiar dacă coeficientul ar fi doar 5, numerele ar trebui să aibă aproximativ 50 de cifre pentru a vedea o îmbunătățire a vitezei.

Pentru copilul meu de 10 ani, înmulțirea numerelor de 400 de cifre ar fi un pic cam greu! Urmărirea diverselor apeluri recursive ale funcției mele ar fi, de asemenea, oarecum descurajantă. Dar pentru un calculator care îndeplinește o sarcină în inteligența artificială sau în fizică, aceasta este o problemă obișnuită!
Cât de profund este acest rezultat?
Ce-mi place la această tehnică este că nu este o știință a rachetelor. Nu este cea mai halucinantă matematică care a fost descoperită vreodată. În retrospectivă, poate că pare evidentă!
Și totuși, aceasta este strălucirea și frumusețea matematicii. Am citit că Kolmogorov a conchis într-un seminar că înmulțirea este în mod fundamental O(n²). Practic, Kolmogorov a inventat o mulțime de teorie și analiză modernă a probabilităților. A fost unul dintre marii matematicieni ai secolului XX. Cu toate acestea, când a venit vorba de acest domeniu fără legătură, s-a dovedit că exista un întreg corpus de cunoștințe care aștepta să fie descoperit, așezat chiar sub nasul său și al tuturor celorlalți!”
De fapt, algoritmii de împărțire și cucerire ne vin în minte destul de repede astăzi, deoarece sunt atât de frecvent utilizați. Dar ei sunt un produs al revoluției computerelor, în sensul că abia cu o putere de calcul imensă mințile umane s-au concentrat în mod specific asupra vitezei de calcul ca domeniu al matematicii demn de a fi studiat de sine stătător.
De aceea, matematicienii nu sunt dispuși să accepte că Ipoteza Riemann este adevărată doar pentru că li se pare că ar putea fi adevărată, sau că P nu este egal cu NP doar pentru că așa pare cel mai probabil. Minunata lume a matematicii păstrează întotdeauna capacitatea de a ne confunda așteptările.
De fapt, puteți găsi modalități și mai rapide de a înmulți. Cele mai bune abordări actuale folosesc transformările Fourier rapide. Dar voi păstra asta pentru o altă zi 🙂
Să-mi spuneți ce părere aveți mai jos. Sunt mai nou pe Twitter ca ethan_the_mathmo, mă puteți urmări aici.
Am dat peste această problemă într-o carte minunată pe care o folosesc, numită „The Nature of Computation” de fizicienii Moore și Mertens, unde una dintre probleme te ghidează prin analiza algoritmului lui Toom.
.