Când datele sunt pregătite pentru a fi analizate, ar trebui să se evalueze temeinic, pe baza inspecției datelor, dacă ar trebui să se utilizeze metode statistice pentru tratarea datelor lipsă. Bell et al. și-au propus să evalueze amploarea și modul de tratare a datelor lipsă în studiile clinice randomizate publicate între iulie și decembrie 2013 în BMJ, JAMA, Lancet și New England Journal of Medicine . 95 % din cele 77 de studii identificate au raportat unele date de rezultat lipsă. Cea mai frecvent utilizată metodă de tratare a datelor lipsă în analiza primară a fost analiza completă a cazurilor (45 %), imputația unică (27 %), metodele bazate pe model (de exemplu, modele mixte sau ecuații de estimare generalizate) (19 %) și imputația multiplă (8 %) .
Analiza completă a cazurilor
Analiza completă a cazurilor este o analiză statistică bazată pe participanți cu un set complet de date de rezultat. Participanții cu orice date lipsă sunt excluși din analiză. După cum este descris în introducere, dacă datele lipsă sunt MCAR, analiza de caz completă va avea o putere statistică redusă din cauza dimensiunii reduse a eșantionului, dar datele observate nu vor fi distorsionate . Atunci când datele lipsă nu sunt MCAR, estimarea analizei cazului complet a efectului intervenției ar putea fi bazată, adică va exista adesea un risc de supraestimare a beneficiilor și de subestimare a daunelor . Vă rugăm să consultați secțiunea „Ar trebui să se utilizeze imputația multiplă pentru a trata datele lipsă?” pentru o discuție mai detaliată a validității potențiale în cazul în care se aplică analiza de caz completă.
Imputație unică
Când se utilizează imputația unică, valorile lipsă sunt înlocuite cu o valoare definită de o anumită regulă . Există mai multe forme de imputare unică, de exemplu, ultima observație reportată (valorile lipsă ale unui participant sunt înlocuite cu ultima valoare observată a participantului), cea mai proastă observație reportată (valorile lipsă ale unui participant sunt înlocuite cu cea mai proastă valoare observată a participantului) și imputare medie simplă . În cazul imputării medii simple, valorile lipsă sunt înlocuite cu media pentru variabila respectivă . Utilizarea imputației simple duce adesea la o subestimare a variabilității, deoarece fiecare valoare neobservată are aceeași pondere în analiză ca și valorile cunoscute, observate . Valabilitatea imputației unice nu depinde de faptul că datele sunt MCAR; imputația unică depinde mai degrabă de ipoteze specifice conform cărora valorile lipsă, de exemplu, sunt identice cu ultima valoare observată . Aceste ipoteze sunt adesea nerealiste și, prin urmare, imputarea unică este adesea o metodă potențial părtinitoare și ar trebui utilizată cu mare prudență .
Imputarea multiplă
Imputarea multiplă s-a dovedit a fi o metodă generală valabilă pentru tratarea datelor lipsă în studiile clinice randomizate, iar această metodă este disponibilă pentru majoritatea tipurilor de date . În secțiunile următoare vom descrie când și cum ar trebui utilizată imputația multiplă.
Ar trebui utilizată imputația multiplă pentru a trata datele lipsă?
Motive pentru care imputația multiplă nu ar trebui să fie utilizată pentru a trata datele lipsă
Este validă ignorarea datelor lipsă?
Analiza datelor observate (analiza cazurilor complete) ignorând datele lipsă este o soluție validă în trei circumstanțe.
- a)
Analiza cazurilor complete poate fi utilizată ca analiză primară dacă proporțiile de date lipsă sunt sub aproximativ 5% (ca regulă generală) și nu este plauzibil ca anumite grupuri de pacienți (de exemplu, participanții foarte bolnavi sau participanții foarte „sănătoși”) să fie în mod specific pierdute la urmărire în unul dintre grupurile comparate . Cu alte cuvinte, dacă impactul potențial al datelor lipsă este neglijabil, atunci datele lipsă pot fi ignorate în analiză . În cazul în care există îndoieli, se pot utiliza analize de sensibilitate în cel mai bun și cel mai rău caz și în cel mai rău caz: mai întâi se generează un set de date cu scenariul „cel mai bun și cel mai rău caz”, în care se presupune că toți participanții pierduți la urmărire din unul dintre grupuri (denumit grupul 1) au avut un rezultat benefic (de exemplu, nu au avut niciun eveniment advers grav); și toți cei cu rezultate lipsă din celălalt grup (grupul 2) au avut un rezultat dăunător (de exemplu, au avut un eveniment advers grav) . Apoi, se generează un set de date cu scenariul „cel mai pesimist”, în care se presupune că toți participanții pierduți la urmărire din grupul 1 au avut un rezultat dăunător; și că toți cei pierduți la urmărire din grupul 2 au avut un rezultat benefic . În cazul în care se utilizează rezultate continue, atunci un „rezultat benefic” ar putea fi media grupului plus 2 deviații standard (sau 1 deviație standard) din media grupului, iar un „rezultat dăunător” ar putea fi media grupului minus 2 deviații standard (sau 1 deviație standard) din media grupului. În cazul datelor dihotomizate, aceste analize de sensibilitate „cel mai bun – cel mai rău” și „cel mai rău – cel mai bun caz” vor arăta apoi intervalul de incertitudine datorat datelor lipsă, iar dacă acest interval nu dă rezultate contradictorii din punct de vedere calitativ, atunci datele lipsă pot fi ignorate. Pentru datele continue, imputarea cu 2 SD va reprezenta un interval posibil de incertitudine având în vedere 95% din datele observate (dacă sunt distribuite normal).
- b)
Dacă numai variabila dependentă are valori lipsă și nu sunt identificate variabile auxiliare (variabile neincluse în analiza de regresie, dar corelate cu o variabilă cu valori lipsă și/sau legate de lipsa acesteia), analiza de caz completă poate fi utilizată ca analiză primară și nu ar trebui să se utilizeze metode specifice pentru a trata datele lipsă . Nu se vor obține informații suplimentare, de exemplu, prin utilizarea imputației multiple, dar erorile standard pot crește din cauza incertitudinii introduse de imputația multiplă .
- c)
După cum s-a menționat mai sus (a se vedea Metode de tratare a datelor lipsă), ar fi, de asemenea, valabil să se efectueze doar analiza cazurilor complete dacă este relativ sigur că datele sunt MCAR (a se vedea Introducere). Este relativ rar cazul în care este sigur că datele sunt MCAR. Este posibil să se testeze ipoteza că datele sunt MCAR cu testul lui Little , dar ar putea fi imprudent să se bazeze pe teste care s-au dovedit a fi nesemnificative. Prin urmare, dacă există o îndoială rezonabilă dacă datele sunt MCAR, chiar dacă testul lui Little este nesemnificativ (nu reușește să respingă ipoteza nulă că datele sunt MCAR), atunci MCAR nu ar trebui să fie asumată.
Sunt proporțiile de date lipsă prea mari?
Dacă lipsesc proporții mari de date, ar trebui să se ia în considerare doar să se raporteze rezultatele analizei complete a cazului și apoi să se discute în mod clar limitările interpretative rezultate din interpretarea rezultatelor studiului. În cazul în care se utilizează imputații multiple sau alte metode pentru a trata datele lipsă, s-ar putea indica faptul că rezultatele studiului sunt confirmative, ceea ce nu este cazul dacă numărul de date lipsă este considerabil. În cazul în care proporțiile de date lipsă sunt foarte mari (de exemplu, mai mult de 40 %) pentru variabile importante, atunci rezultatele trialului pot fi considerate doar ca rezultate generatoare de ipoteze . O excepție rară ar fi în cazul în care mecanismul care stă la baza datelor lipsă poate fi descris ca fiind MCAR (a se vedea punctul de mai sus).
Apoi ipoteza MCAR și ipoteza MAR par amândouă neverosimile?
Dacă ipoteza MAR pare neverosimilă pe baza caracteristicilor datelor lipsă, atunci rezultatele studiului vor fi expuse riscului de a obține rezultate distorsionate din cauza „distorsiunii datelor incomplete privind rezultatele” și nicio metodă statistică nu poate ține seama cu certitudine de această potențială distorsiune . Validitatea metodelor utilizate pentru a trata datele MNAR necesită anumite ipoteze care nu pot fi testate pe baza datelor observate. Analizele de sensibilitate în cel mai bun și cel mai rău caz și în cel mai rău caz pot arăta întreaga gamă teoretică de incertitudine, iar concluziile ar trebui să fie legate de această gamă de incertitudine. Limitările analizelor ar trebui să fie discutate și luate în considerare în mod amănunțit.
Variabila de rezultat cu valori lipsă este continuă și modelul analitic este complicat (de exemplu, cu interacțiuni)?
În această situație, se poate lua în considerare utilizarea metodei maxime de verosimilitate directă pentru a evita problemele de compatibilitate a modelului între modelul analitic și modelul de imputare multiplă, în cazul în care primul este mai general decât cel de-al doilea. În general, se pot utiliza metodele de verosimilitate maximă directă, dar, după cunoștințele noastre, metodele disponibile în comerț sunt în prezent disponibile numai pentru variabilele continue.
Când și cum să se utilizeze imputațiile multiple
Dacă nu este îndeplinit niciunul dintre „Motivele pentru care nu ar trebui să se utilizeze imputația multiplă pentru a trata datele lipsă” de mai sus, atunci ar putea fi utilizată imputația multiplă. Diferite proceduri au fost sugerate în literatura de specialitate în ultimele câteva decenii pentru a trata datele lipsă . Am prezentat considerațiile menționate mai sus cu privire la metodele statistice de tratare a datelor lipsă în Fig. 1.
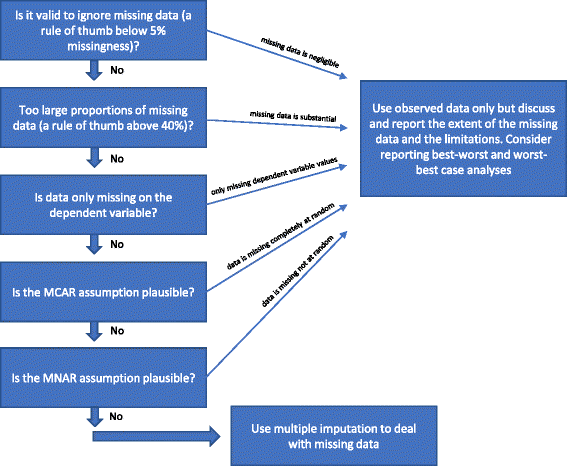
Flowchart: când ar trebui utilizată imputația multiplă pentru a trata datele lipsă atunci când se analizează rezultatele studiilor clinice randomizate
Imputația multiplă își are originea la începutul anilor 1970 și a câștigat o popularitate din ce în ce mai mare de-a lungul anilor . Imputarea multiplă este o tehnică statistică bazată pe simulare pentru tratarea datelor lipsă . Imputarea multiplă constă în trei etape:
-
Etapa de imputare. O „imputare” reprezintă, în general, un set de valori plauzibile pentru datele lipsă – imputarea multiplă reprezintă mai multe seturi de valori plauzibile . Atunci când se utilizează imputația multiplă, valorile lipsă sunt identificate și sunt înlocuite cu un eșantion aleatoriu de imputații de valori plauzibile (seturi de date completate). Seturile multiple de date completate sunt generate prin intermediul unui anumit model de imputare ales . Cinci seturi de date imputate au fost sugerate în mod tradițional ca fiind suficiente din motive teoretice, dar 50 de seturi de date (sau mai multe) par a fi preferabile pentru a reduce variabilitatea de eșantionare din procesul de imputare .
-
Etapa de analiză a datelor completate (estimare). Analiza dorită se efectuează separat pentru fiecare set de date care este generat în timpul etapei de imputare . Astfel, de exemplu, se construiesc 50 de rezultate de analiză.
-
Etapa de punere în comun. Rezultatele obținute din fiecare analiză a datelor completate sunt combinate într-un singur rezultat de imputare multiplă . Nu este necesar să se efectueze o meta-analiză ponderată, deoarece se consideră că toate spun 50 de rezultate de analiză au aceeași pondere statistică.
Este de mare importanță fie că există compatibilitate între modelul de imputare și modelul de analiză, fie că modelul de imputare este mai general decât modelul de analiză (de exemplu, că modelul de imputare include mai multe covariate independente decât modelul de analiză) . De exemplu, dacă modelul de analiză are interacțiuni semnificative, atunci modelul de imputare ar trebui să le includă și pe acestea , dacă modelul de analiză utilizează o versiune transformată a unei variabile, atunci modelul de imputare ar trebui să utilizeze aceeași transformare , etc.
Diferite tipuri de imputare multiplă
Există diferite tipuri de metode de imputare multiplă. Le vom prezenta în funcție de gradele lor crescânde de complexitate: 1) analiza de regresie cu valoare unică; 2) imputare monotonă; 3) ecuații înlănțuite sau metoda Markov chain Monte Carlo (MCMC). În paragrafele următoare vom descrie aceste diferite metode de imputare multiplă și modul de alegere între ele.
O analiză de regresie cu o singură valoare include o variabilă dependentă și variabilele de stratificare utilizate în randomizare. Variabilele de stratificare includ adesea un indicator de centru dacă studiul este un studiu multicentric și, de obicei, una sau mai multe variabile de ajustare cu informații prognostice care sunt corelate cu rezultatul. În cazul în care se utilizează o variabilă dependentă continuă, se poate include, de asemenea, o valoare inițială a variabilei dependente. După cum se menționează la „Motive pentru care nu ar trebui să se utilizeze metode statistice pentru tratarea datelor lipsă”, în cazul în care numai variabila dependentă are valori lipsă și nu sunt identificate variabile auxiliare, ar trebui efectuată o analiză completă a cazului și nu ar trebui să se utilizeze metode specifice pentru tratarea datelor lipsă. În cazul în care au fost identificate variabile auxiliare, se poate efectua o imputație cu o singură variabilă. În cazul în care există date lipsă semnificative în ceea ce privește variabila de bază a unei variabile continue, o analiză completă a cazului poate furniza rezultate distorsionate . Prin urmare, în toate cazurile, se efectuează o imputare cu o singură variabilă (cu sau fără variabile auxiliare incluse, după caz) dacă doar variabila de bază lipsește.
Dacă atât variabila dependentă, cât și variabila de bază lipsesc și lipsa este monotonă, se efectuează o imputare monotonă. Să presupunem o matrice de date în care pacienții sunt reprezentați prin rânduri și variabilele prin coloane. Se spune că lipsa unei astfel de matrice de date este monotonă dacă coloanele sale pot fi reordonate astfel încât, pentru orice pacient, (a) dacă o valoare lipsește, toate valorile din dreapta poziției sale sunt, de asemenea, lipsă, și (b) dacă o valoare este observată, toate valorile din stânga acestei valori sunt, de asemenea, observate. În cazul în care lipsa este monotonă, metoda de imputare multiplă este, de asemenea, relativ simplă, chiar dacă mai mult de o variabilă are valori lipsă . În acest caz, este relativ simplu să se impută datele lipsă utilizând imputarea prin regresie secvențială, în care valorile lipsă sunt imputate pentru fiecare variabilă în parte . Multe pachete statistice (de exemplu, STATA) pot analiza dacă lipsa este monotonă sau nu.
În cazul în care lipsa nu este monotonă, se efectuează o imputare multiplă utilizând ecuațiile înlănțuite sau metoda MCMC. Variabilele auxiliare sunt incluse în model în cazul în care acestea sunt disponibile. Am rezumat modul de alegere între diferitele metode de imputare multiplă în Fig. 2.
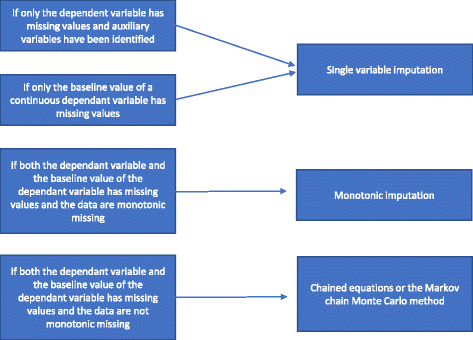
Flowchart of multiple imputation
Full information maximum likelihood
Full information maximum likelihood este o metodă alternativă de tratare a datelor lipsă . Principiul estimării maximului de verosimilitate este de a estima parametrii distribuției comune a rezultatului (Y) și a covariatelor (X1,…, Xk) care, dacă ar fi adevărate, ar maximiza probabilitatea de a observa valorile pe care le-am observat de fapt . În cazul în care valorile lipsesc la un anumit pacient, putem obține probabilitatea prin însumarea probabilității obișnuite pentru toate valorile posibile ale datelor lipsă, cu condiția ca mecanismul datelor lipsă să fie ignorabil. Această metodă este denumită probabilitate maximă cu informații complete .
Verosimilitudinea maximă cu informații complete are atât puncte forte, cât și limitări în comparație cu imputația multiplă.
Potriviri ale verosimilitudinii maxime cu informații complete în comparație cu imputația multiplă
- 1)
Este mai simplu de implementat, adică. nu este necesar să se parcurgă diferite etape ca atunci când se utilizează imputația multiplă.
- 2)
În comparație cu imputația multiplă, verosimilitatea maximă cu informații complete nu are probleme potențiale de incompatibilitate între modelul de imputare și modelul de analiză (a se vedea „Imputația multiplă”). Validitatea rezultatelor imputației multiple va fi pusă sub semnul întrebării în cazul în care există o incompatibilitate între modelul de imputare și modelul de analiză sau dacă modelul de imputare este mai puțin general decât modelul de analiză .
- 3)
Când se utilizează imputarea multiplă, toate valorile lipsă din fiecare set de date generat (etapa de imputare) sunt înlocuite cu un eșantion aleatoriu de valori plauzibile . Prin urmare, dacă nu se specifică „o sămânță aleatorie”, de fiecare dată când se efectuează o analiză de imputare multiplă vor fi afișate rezultate diferite . Analizele atunci când se utilizează maximum de verosimilitate cu informații complete pe același set de date vor produce aceleași rezultate de fiecare dată când se efectuează analiza și, prin urmare, rezultatele nu depind de o sămânță de numere aleatoare. Cu toate acestea, în cazul în care valoarea sămânței aleatoare este definită în planul de analiză statistică, această problemă poate fi rezolvată.
Limitele utilizării verosimilitudinii maxime cu informații complete în comparație cu imputația multiplă
Limitele utilizării verosimilitudinii maxime cu informații complete în comparație cu utilizarea imputației multiple, este că utilizarea verosimilitudinii maxime cu informații complete este posibilă numai cu ajutorul unui software special conceput . Au fost dezvoltate programe software preliminare proiectate, dar majoritatea acestora nu dispun de caracteristicile programelor statistice proiectate în comerț (de exemplu, STATA, SAS sau SPSS). În STATA (utilizând comanda SEM) și SAS (utilizând comanda PROC CALIS), este posibilă utilizarea probabilității maxime cu informații complete, dar numai atunci când se utilizează variabile dependente (rezultate) continue. Pentru regresia logistică și regresia Cox, singurul pachet comercial care oferă maximum de verosimilitate cu informații complete pentru datele lipsă este Mplus.
O altă limitare potențială atunci când se utilizează maximum de verosimilitate cu informații complete este că poate exista o presupunere de normalitate multivariată subiacentă . Cu toate acestea, este posibil ca încălcările ipotezei normalității multivariate să nu fie atât de importante, astfel încât ar putea fi acceptabilă includerea variabilelor independente binare în analiză .
Am inclus în fișierul suplimentar 1 un program (SAS) care produce un set complet de date de jucărie care include mai multe analize diferite ale acestor date. Tabelul 1 și Tabelul 2 arată rezultatul și modul în care diferite metode care tratează datele lipsă produc rezultate diferite.
Analiza de regresie a valorilor de panel
Datele de panel sunt de obicei conținute într-un așa-numit fișier de date larg, în care primul rând conține numele variabilelor, iar rândurile ulterioare (unul pentru fiecare pacient) conțin valorile corespunzătoare. Rezultatul este reprezentat de variabile diferite – una pentru fiecare măsurătoare planificată și cronometrată a rezultatului. Pentru a analiza datele, trebuie să se convertească fișierul într-un așa-numit fișier lung, cu o înregistrare pentru fiecare măsurătoare planificată a rezultatului, inclusiv valoarea rezultatului, momentul măsurătorii și o copie a tuturor celorlalte valori ale variabilelor, cu excepția celor ale variabilei rezultatului. Pentru a păstra corelațiile în interiorul pacientului între măsurătorile de rezultat cronometrate, este o practică obișnuită să se efectueze o calculare multiplă a fișierului de date în forma sa largă, urmată de o analiză a fișierului rezultat după ce acesta a fost convertit în forma sa lungă. Proc mixed (SAS 9.4) poate fi utilizat pentru analiza valorilor rezultatelor continue, iar proc. glimmix (SAS 9.4) pentru alte tipuri de rezultate. Deoarece aceste proceduri aplică metoda directă de maximă verosimilitate asupra datelor de rezultat, dar ignoră cazurile cu valori lipsă ale covariatelor, procedurile pot fi utilizate direct atunci când lipsesc doar valorile variabilei dependente și nu sunt disponibile variabile auxiliare bune. În caz contrar, ar trebui să se utilizeze proc. mixed sau proc. glimmix (oricare dintre acestea este adecvată) după o calculare multiplă. În mod evident, o abordare corespunzătoare poate fi posibilă folosind alte pachete statistice.
Analize de sensibilitate
Analizele de sensibilitate pot fi definite ca un set de analize în care datele sunt tratate într-un mod diferit față de analiza primară. Analizele de sensibilitate pot arăta modul în care ipotezele, diferite de cele făcute în analiza primară, influențează rezultatele obținute . Analizele de sensibilitate ar trebui să fie predefinite și descrise în planul de analiză statistică, dar ar putea fi justificate și valabile analize de sensibilitate post hoc suplimentare. Atunci când influența potențială a valorilor lipsă este neclară, recomandăm următoarele analize de sensibilitate:
-
Am descris deja utilizarea analizelor de sensibilitate în cel mai bun și cel mai rău caz și în cel mai rău caz pentru a arăta intervalul de incertitudine datorat datelor lipsă (a se vedea Evaluarea măsurii în care ar trebui să se utilizeze metode pentru a gestiona datele lipsă). Descrierea noastră anterioară a analizelor de sensibilitate în cel mai bun și cel mai rău caz și în cel mai rău caz a fost legată de datele lipsă fie pe o variabilă dependentă dihotomică, fie pe o variabilă dependentă continuă, dar aceste analize de sensibilitate pot fi utilizate și atunci când lipsesc date privind variabilele de stratificare, valorile de referință etc. Influența potențială a datelor lipsă ar trebui evaluată pentru fiecare variabilă în parte, adică ar trebui să existe un scenariu cel mai bun – cel mai rău și un scenariu cel mai rău – cel mai bun pentru fiecare variabilă (variabila dependentă, indicatorul de rezultat și variabilele de stratificare) cu date lipsă.
-
Dacă se decide că, de exemplu, ar trebui să se utilizeze imputații multiple, atunci aceste rezultate ar trebui să fie rezultatul principal al rezultatului dat. Fiecare analiză primară de regresie ar trebui să fie întotdeauna completată de o analiză corespunzătoare a cazurilor observate (sau disponibile).
Când se utilizează metode cu efecte mixte
Utilizarea unui proiect de studiu multicentric va fi adesea necesară pentru a recruta un număr suficient de participanți la studiu într-un interval de timp rezonabil . Un proiect de studiu multicentric oferă, de asemenea, o bază mai bună pentru generalizarea ulterioară a constatărilor sale . S-a demonstrat că cele mai frecvent utilizate metode de analiză în studiile clinice randomizate au performanțe bune cu un număr mic de centre (analizând rezultate dependente binare) . În cazul unui număr relativ mare de centre (50 sau mai multe), este adesea optimă utilizarea „centrului” ca efect aleatoriu și utilizarea metodelor de analiză a efectelor mixte. De asemenea, va fi adesea validă utilizarea metodelor de analiză cu efecte mixte atunci când se analizează date longitudinale . În anumite circumstanțe, ar putea fi valabil să se includă covariabila cu „efect aleatoriu” (de exemplu, „centru”) ca o covariabilă cu efect fix în timpul etapei de imputare și apoi să se utilizeze o analiză cu model mixt sau ecuații de estimare generalizată (GEE) în timpul etapei de analiză . Cu toate acestea, aplicarea unui model cu efecte mixte (cu, de exemplu, „centru” ca efect aleatoriu) implică faptul că structura multistratificată a datelor trebuie să fie luată în considerare la modelarea imputației multiple. În prezent, software-ul comercial nu este direct disponibil pentru a face acest lucru. Cu toate acestea, se poate utiliza pachetul REALCOME, care poate fi interfațat cu STATA . Interfața exportă datele cu valori lipsă din STATA în REALCOM, unde imputarea se face ținând cont de natura pe mai multe niveluri a datelor și utilizând o metodă MCMC care include variabilele continue și, prin utilizarea unui model normal latent, permite, de asemenea, o tratare adecvată a datelor discrete. Seturile de date imputate pot fi apoi analizate cu ajutorul comenzii STATA „mi estimate:”, care poate fi combinată cu instrucțiunea „mixed” (pentru un rezultat continuu) sau cu instrucțiunea „meqrlogit” pentru rezultate binare sau ordinale în STATA . Cu toate acestea, în cadrul analizei datelor de panel, ne putem confrunta cu ușurință cu o situație în care datele includ trei sau mai multe niveluri, de exemplu, măsurători în cadrul aceluiași pacient (nivel 1), pacienți în cadrul centrelor (nivel 2) și centre (nivel 3) . Pentru a nu ne implica într-un model destul de complicat care poate duce la lipsa de convergență sau la erori standard instabile și pentru care nu este disponibil un software comercial, am recomanda fie tratarea efectului de centru ca fiind fix (direct sau în urma fuzionării centrelor mici într-unul sau mai multe centre de dimensiuni adecvate, folosind o procedură care trebuie prescrisă în planul de analiză statistică), fie excluderea centrului ca o covariabilă. În cazul în care randomizarea a fost stratificată în funcție de centru, această din urmă abordare va conduce la o distorsiune în sus a erorilor standard, ceea ce va duce la o procedură de testare oarecum conservatoare .