Recent, un coleg mi-a pus câteva întrebări de genul „de ce avem atât de multe funcții de activare?”, „de ce una funcționează mai bine decât cealaltă?”, „cum știm pe care să o folosim?”, „este o matematică dură?” și așa mai departe. Așa că m-am gândit, de ce să nu scriu un articol pe această temă pentru cei care sunt familiarizați cu rețelele neuronale doar la un nivel de bază și care, prin urmare, se întreabă despre funcțiile de activare și despre „de ce-cum-matematica lor!”.
NOTA: Acest articol presupune că aveți cunoștințe de bază despre un „neuron” artificial. V-aș recomanda să citiți elementele de bază ale rețelelor neuronale înainte de a citi acest articol, pentru o mai bună înțelegere.
Funcții de activare
Atunci ce face un neuron artificial? Pur și simplu, calculează o „sumă ponderată” a intrărilor sale, adaugă o polarizare și apoi decide dacă ar trebui să fie „concediat” sau nu ( da, corect, o funcție de activare face acest lucru, dar haideți să mergem pe firul curentului pentru un moment ).
Considerăm deci un neuron.
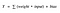
Acum, valoarea lui Y poate fi orice variind de la -inf la +inf. Neuronul nu cunoaște cu adevărat limitele valorii. Deci, cum decidem dacă neuronul ar trebui să tragă sau nu ( de ce acest model de tragere? Pentru că am învățat din biologie că așa funcționează creierul, iar creierul este o mărturie funcțională a unui sistem minunat și inteligent).
Am decis să adăugăm „funcții de activare” în acest scop. Pentru a verifica valoarea Y produsă de un neuron și a decide dacă conexiunile exterioare ar trebui să considere acest neuron ca fiind „tras” sau nu. Sau mai degrabă să spunem – „activat” sau nu.
Funcție de activare
Primul lucru care ne vine în minte este ce zici de o funcție de activare bazată pe prag? Dacă valoarea lui Y este peste o anumită valoare, să o declarăm activată. Dacă este mai mică decât pragul, atunci declarăm că nu este activată. Hmm grozav. Acest lucru ar putea funcționa!
Funcția de activare A = „activată” dacă Y > prag altfel nu
Alternativ, A = 1 dacă y> prag, 0 altfel
Bine, ceea ce tocmai am făcut este o „funcție în trepte”, vezi figura de mai jos.
Să iasă 1 ( activat) când valoarea > 0 (prag) și iese un 0 ( neactivat) în caz contrar.
Genial. Deci, aceasta face o funcție de activare pentru un neuron. Fără confuzii. Cu toate acestea, există totuși anumite dezavantaje cu acest lucru. Pentru a înțelege mai bine, gândiți-vă la următoarele.
Să presupunem că creați un clasificator binar. Ceva care ar trebui să spună un „da” sau „nu” ( activați sau nu activați ). O funcție Step ar putea face asta pentru dumneavoastră! Asta este exact ceea ce face, spune un 1 sau 0. Acum, gândiți-vă la cazul de utilizare în care ați dori ca mai mulți astfel de neuroni să fie conectați pentru a aduce mai multe clase. Clasa1, clasa2, clasa3 etc. Ce se va întâmpla dacă mai mult de 1 neuron este „activat”. Toți neuronii vor emite un 1 ( din funcția de pas). Acum ce ați decide? Care este clasa? Hmm greu, complicat.
Ați dori ca rețeaua să activeze doar 1 neuron, iar ceilalți să fie 0 ( numai atunci ați putea spune că a clasificat corect/identificat clasa ). Ah!!! Este mai greu de antrenat și de convergent în acest fel. Ar fi fost mai bine dacă activarea nu ar fi fost binară și ar fi spus în schimb „50% activat” sau „20% activat” și așa mai departe. Și apoi, dacă mai mult de 1 neuron se activează, ați putea găsi care neuron are „cea mai mare activare” și așa mai departe ( mai bine decât max, un softmax, dar să lăsăm asta deocamdată ).
În acest caz, de asemenea, dacă mai mult de 1 neuron spune „100% activat”, problema persistă în continuare.știu! Dar..din moment ce există valori intermediare de activare pentru ieșire, învățarea poate fi mai lină și mai ușoară ( mai puțin agitată ) și șansele ca mai mult de 1 neuron să fie 100% activat sunt mai mici în comparație cu funcția în trepte în timpul antrenamentului ( de asemenea, în funcție de ceea ce se antrenează și de date ).
Ok, deci vrem ceva care să ne dea valori intermediare ( analogice ) de activare în loc să spună „activat” sau nu ( binar ).
Primul lucru care ne vine în minte ar fi funcția liniară.
Funcție liniară
A = cx
O funcție de linie dreaptă în care activarea este proporțională cu intrarea ( care este suma ponderată de la neuron ).
În acest fel, oferă o gamă de activări, deci nu este o activare binară. Putem conecta cu siguranță câțiva neuroni împreună și dacă se activează mai mult de 1, am putea lua maximul ( sau softmax) și să decidem pe baza acestuia. Deci și acest lucru este în regulă. Atunci care este problema?
Dacă sunteți familiarizați cu coborârea gradientului pentru instruire, veți observa că pentru această funcție, derivata este o constantă.
A = cx, derivata în raport cu x este c. Asta înseamnă că gradientul nu are nicio relație cu X. Este un gradient constant și coborârea se va face pe gradient constant. În cazul în care există o eroare de predicție, modificările efectuate prin propagare inversă sunt constante și nu depind de modificarea intrării delta(x) !!!
Aceasta nu este atât de bună! ( nu întotdeauna, dar aveți răbdare cu mine ). Mai există și o altă problemă. Gândiți-vă la straturile conectate. Fiecare strat este activat de o funcție liniară. Această activare, la rândul ei, intră în nivelul următor ca intrare, iar al doilea strat calculează suma ponderată pe această intrare și, la rândul său, se declanșează pe baza unei alte funcții de activare liniare.
Nu contează câte straturi avem, dacă toate sunt de natură liniară, funcția de activare finală a ultimului strat nu este altceva decât o funcție liniară a intrării primului strat! Faceți o mică pauză și gândiți-vă la asta.
Aceasta înseamnă că aceste două straturi ( sau N straturi ) pot fi înlocuite cu un singur strat. Ah! Tocmai am pierdut capacitatea de suprapunere a straturilor în acest fel. Indiferent de modul în care suprapunem, întreaga rețea este în continuare echivalentă cu un singur strat cu activare liniară ( o combinație de funcții liniare într-o manieră liniară este tot o altă funcție liniară ).
Să mergem mai departe, da?
Funcția Sigmoid
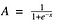
Bine, aceasta pare netedă și „asemănătoare unei funcții în trepte”. Care sunt avantajele acestui lucru? Gândiți-vă puțin la asta. Mai întâi de toate, este de natură neliniară. Combinațiile acestei funcții sunt, de asemenea, neliniare! Minunat. Acum putem suprapune straturi. Cum rămâne cu activările non-binare? Da, și asta!. Aceasta va da o activare analogică, spre deosebire de funcția în trepte. Are și un gradient neted.
Și dacă observați, între valorile X de la -2 la 2, valorile Y sunt foarte abrupte. Ceea ce înseamnă că orice schimbare mică a valorilor lui X în acea regiune va determina ca valorile lui Y să se schimbe semnificativ. Ah, asta înseamnă că această funcție are tendința de a aduce valorile Y la ambele capete ale curbei.
Se pare că este bună pentru un clasificator având în vedere proprietatea sa? Da !!! Într-adevăr, așa este. Ea are tendința de a aduce activările la ambele părți ale curbei ( peste x = 2 și sub x = -2, de exemplu). Făcând distincții clare la predicție.
Un alt avantaj al acestei funcții de activare este că, spre deosebire de funcția liniară, ieșirea funcției de activare va fi întotdeauna în intervalul (0,1) în comparație cu (-inf, inf) a funcției liniare. Așadar, avem activările noastre delimitate într-un interval. Frumos, nu va arunca în aer activările atunci.
Este grozav. Funcțiile Sigmoid sunt una dintre cele mai utilizate funcții de activare în prezent. Atunci care sunt problemele cu aceasta?
Dacă observați, spre oricare dintre capetele funcției sigmoide, valorile Y tind să răspundă foarte puțin la schimbările în X. Ce înseamnă asta? Gradientul în acea regiune va fi mic. Aceasta dă naștere la o problemă de „gradienți care dispar”. Hmm. Deci, ce se întâmplă atunci când activările ajung aproape de partea „aproape orizontală” a curbei de o parte și de alta?
Gradientul este mic sau a dispărut ( nu poate face schimbări semnificative din cauza valorii extrem de mici ). Rețeaua refuză să învețe mai departe sau este drastic de lentă ( în funcție de cazul de utilizare și până când gradientul /calculul se lovește de limitele valorilor în virgulă mobilă ). Există modalități de a ocoli această problemă, iar sigmoidul este încă foarte popular în problemele de clasificare.
Funcția Tanh
O altă funcție de activare care este utilizată este funcția tanh.
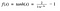
Hm. Aceasta arată foarte asemănător cu sigmoidul. De fapt, este o funcție sigmoidă scalată!

Ok, acum aceasta are caracteristici similare cu sigmoida pe care am discutat-o mai sus. Este de natură neliniară, deci minunat că putem suprapune straturi! Este limitată la intervalul (-1, 1), astfel încât nu trebuie să ne facem griji cu privire la activările care explodează. Un aspect care trebuie menționat este că gradientul este mai puternic pentru tanh decât pentru sigmoid (derivatele sunt mai abrupte). Decizia de a alege între sigmoid sau tanh va depinde de cerința dumneavoastră privind puterea gradientului. Ca și sigmoidul, tanh are și ea problema gradientului care dispare.
Tanh este, de asemenea, o funcție de activare foarte populară și utilizată pe scară largă.
ReLu
Mai târziu, vine funcția ReLu,
A(x) = max(0,x)
Funcția ReLu este așa cum este prezentată mai sus. Ea dă o ieșire x dacă x este pozitiv și 0 în caz contrar.
La prima vedere, aceasta ar părea că are aceleași probleme ca și funcția liniară, deoarece este liniară pe axa pozitivă. În primul rând, ReLu este neliniară prin natura sa. Iar combinațiile lui ReLu sunt, de asemenea, neliniare! ( de fapt este un bun aproximator. Orice funcție poate fi aproximată cu combinații de ReLu). Minunat, deci asta înseamnă că putem suprapune straturi. Totuși, nu este legat. Intervalul lui ReLu este [0, inf). Acest lucru înseamnă că poate umfla activarea.
Un alt punct pe care aș dori să-l discut aici este dispersia activării. Imaginați-vă o rețea neuronală mare, cu o mulțime de neuroni. Folosirea unui sigmoid sau tanh va face ca aproape toți neuronii să se activeze într-un mod analogic ( vă amintiți? ). Asta înseamnă că aproape toate activările vor fi procesate pentru a descrie ieșirea unei rețele. Cu alte cuvinte, activarea este densă. Acest lucru este costisitor. Ideal ar fi să ne dorim ca câțiva neuroni din rețea să nu se activeze și astfel să facem activările rare și eficiente.
ReLu ne oferă acest beneficiu. Imaginați-vă o rețea cu greutăți inițializate aleatoriu ( sau normalizate ) și aproape 50% din rețea dă 0 activare din cauza caracteristicii ReLu ( ieșire 0 pentru valori negative ale lui x ). Acest lucru înseamnă că mai puțini neuroni trag ( activare rară ) și rețeaua este mai ușoară. Frumos! ReLu pare să fie minunată! Da, este, dar nimic nu este fără cusur… Nici măcar ReLu.
Din cauza liniei orizontale din ReLu ( pentru X negativ ), gradientul poate merge spre 0. Pentru activările din acea regiune din ReLu, gradientul va fi 0, din cauza căreia ponderile nu vor fi ajustate în timpul coborârii. Asta înseamnă că acei neuroni care intră în acea stare nu vor mai răspunde la variațiile erorii/intrării ( pur și simplu pentru că gradientul este 0, nu se schimbă nimic ). Aceasta se numește problema ReLu muribundă. Această problemă poate face ca mai mulți neuroni să moară pur și simplu și să nu mai răspundă, făcând pasivă o parte substanțială a rețelei. Există variații în ReLu pentru a atenua această problemă prin simpla transformare a liniei orizontale într-o componentă non-orizontală . de exemplu y = 0,01x pentru x<0 va face ca aceasta să fie o linie ușor înclinată mai degrabă decât o linie orizontală. Acesta este ReLu cu scurgeri. Există și alte variante. Ideea principală este de a lăsa gradientul să nu fie zero și să se recupereze în timpul antrenamentului în cele din urmă.
ReLu este mai puțin costisitor din punct de vedere computațional decât tanh și sigmoid deoarece implică operații matematice mai simple. Acesta este un punct bun de luat în considerare atunci când proiectăm rețele neuronale profunde.
Ok, acum pe care o folosim?
Acum, ce funcții de activare să folosim. Asta înseamnă că folosim doar ReLu pentru tot ceea ce facem? Sau sigmoid sau tanh? Ei bine, da și nu. Atunci când știți că funcția pe care încercați să o aproximați are anumite caracteristici, puteți alege o funcție de activare care va aproxima funcția mai rapid, ceea ce duce la un proces de instruire mai rapid. De exemplu, un sigmoid funcționează bine pentru un clasificator (vedeți graficul sigmoidului, nu-i așa că arată proprietățile unui clasificator ideal? ), deoarece aproximarea unei funcții de clasificare sub forma unor combinații de sigmoide este mai ușoară decât poate ReLu, de exemplu. Ceea ce va duce la un proces de instruire și convergență mai rapid. De asemenea, puteți utiliza propriile funcții personalizate!. Dacă nu cunoașteți natura funcției pe care încercați să o învățați, atunci poate că v-aș sugera să începeți cu ReLu și apoi să lucrați în sens invers. ReLu funcționează de cele mai multe ori ca un aproximator general!
În acest articol, am încercat să descriu câteva funcții de activare utilizate în mod obișnuit. Există și alte funcții de activare, dar ideea generală rămâne aceeași. Cercetările pentru funcții de activare mai bune sunt încă în curs de desfășurare. Sper că ați prins ideea din spatele funcției de activare, de ce sunt folosite și cum decidem pe care să o folosim.
.