Wklęsły vs. wypukły?

Jaka jest różnica między wklęsłym a wypukłym?

Jeśli mielibyśmy opisać różnicę między wklęsłym a wypukłym w najbardziej ogólny sposób, powiedzielibyśmy, że każdy pusty, podobny do miski obiekt jest wklęsły, podczas gdy każdy obiekt przypominający piłkę do rugby lub piłkę nożną ma kształt wypukły. Ale być może powodem, dla którego wypukły i wklęsły są tak powszechnie nadużywane jest to, że te dwa słowa nie są tak proste, jak byśmy chcieli, aby były.

Większość źródeł gramatyki kładzie nacisk na to, jak używanie mnemotechnik jest możliwe do rozszyfrowania convex i concave przez słowo cave. Podczas gdy pojęcie kojarzenia wklęsłości z wydarzeniem czegoś „caving-in” pomaga w nauce o cechach powierzchni, to jest mylące, aby odnieść ten pomysł do tematów obejmujących wykresy.

Aby zrozumieć, jak wklęsłe i wypukłe różnią się od siebie, musimy dowiedzieć się, jak każdy termin jest używany w zdolności matematyki, lustra, soczewki, i wreszcie, w ramach twórczego pisania. Kiedy już zdecydujesz, w jakim kontekście chciałbyś używać słów takich jak wklęsły i wypukły, poznanie ich technicznych aspektów pozwoli Ci być bardziej pewnym siebie w używaniu ich w mowie codziennej.

Co oznacza wklęsły?

Wklęsły jest używany jako przymiotnik lub rzeczownik do opisania kształtu przedmiotu lub powierzchni, która jest zakrzywiona do wewnątrz lub wydrążona jak miska. Examples of concave in a sentence include,

„She scooped the ice cream from the container, leaving a concave footprint.”

According to The Oxford Dictionary of Word Histories, the word concave stems from late Middle English. Wklęsłość i wklęsłość oddają łaciński termin concavus (con- i cavus), który tłumaczy się na 'razem’ i 'pusty’ („Concave,” 110).

Synonimy wklęsłości obejmują:

Dented, depressed, dished, hollow, indented, recessed, and sunken.

Antonimy concave include:

Bulwiasty, zakrzywiony, wystający, wystający, wypukły.

Co to znaczy wypukły?

Słowo wypukły, lub wypukłość, jest przymiotnikiem opisującym obiekt lub powierzchnię, która jest zaokrąglona lub zakrzywiona. W odniesieniu do obiektów, środkowa powierzchnia wypukłego obiektu jest szersza niż jego zewnętrzny narożnik. Przykłady wypukłości w zdaniu obejmują,

„Wpadłem w trujący bluszcz i teraz mam czerwone, wypukłe guzy na całej skórze.”

Synonimy convex include:

Łukowate, wygięte, wybrzuszone, uniesione.

Antonimy convex include:

Depresyjny, zapadający się.

Funkcje wklęsłe vs wypukłe

Funkcja wypukła reprezentuje linię ciągłą na wykresie, gdzie punkt środkowy, lub mediana liczby całkowitej dziedziny, nie przekracza średniej przedziału. Funkcja wklęsła jest dokładnym przeciwieństwem funkcji wypukłej, ponieważ, aby f(x) była wklęsła, f(x) musi być ujemna. Aby różnice były bardziej zrozumiałe, poniżej znajduje się krótki opis porównania tych pojęć:

Wklęsła w górę = wypukła = wypukła w dół

Wklęsła w dół = wklęsła = wypukła w górę

Różnicę między funkcjami wklęsłymi i wypukłymi widać wyraźniej, jeśli spojrzymy na wykres. Zauważ, jak funkcja wypukła otwiera się w górę, podczas gdy funkcja wklęsła otwiera się w dół.

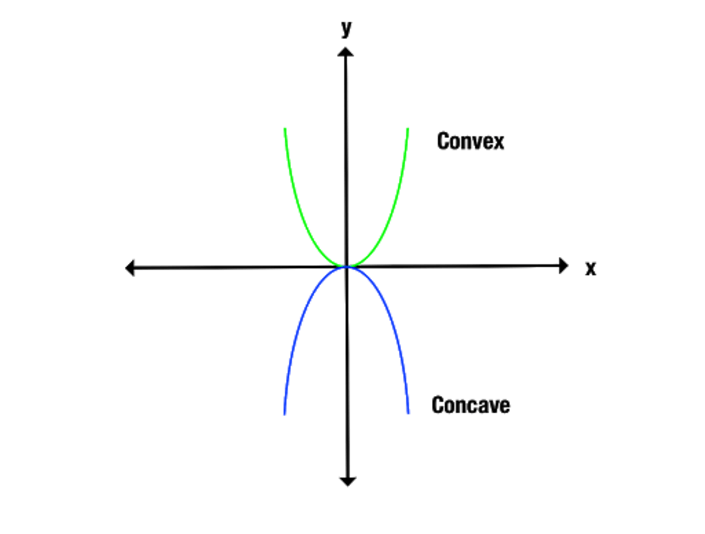
Innym sposobem identyfikacji funkcji wklęsłych i wypukłych jest połączenie punktów na wykresie wzdłuż osi x. Funkcja wklęsła łączy tylko linie poniżej wykresu, podczas gdy funkcja wypukła tworzy tylko linie powyżej wykresu.

Możemy dodatkowo użyć rachunku do rozszyfrowania, czy funkcja jest wypukła czy wklęsła. Jeśli druga pochodna f(x) jest większa od zera, to funkcja jest wypukła. Ale jeśli druga pochodna f(x) jest mniejsza od zera, to funkcja jest wklęsła.

Wypukłe vs. wklęsłe wielokąty

Nie panikuj, ale słowa wypukłe i wklęsłe są również używane w geometrii. Wypukłe i wklęsłe kształty są najczęściej omawiane w odniesieniu do wielokątów, które są kształtami z minimum trzema bokami i kątami.

Regularne wielokąty istnieją z równymi bokami i kątami, ale wypukłe i wklęsłe wielokąty są nieco bardziej skomplikowane. Wielokąty wypukłe zawierają kąty wewnętrzne, które są mniejsze niż 180 stopni, natomiast wielokąty wklęsłe zawierają jeden lub więcej kątów wewnętrznych, które są większe niż 180 stopni.

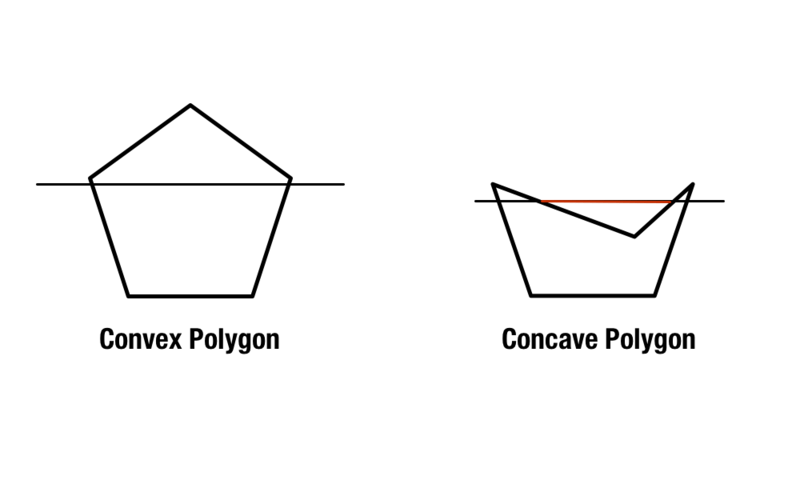
Drugą metodą identyfikacji wielokątów wklęsłych i wypukłych jest narysowanie dwóch ukośnych linii w poprzek kształtu, zaczynając od jego rogów. Jeśli każda linia istnieje wewnątrz kształtu, kształt jest wypukły. Jeśli jest co najmniej jedna linia, która przecina poza kształtem, to jest on wklęsły.

Wklęsłe vs. wypukłe lustra

Słowa wklęsłe i wypukłe są powszechnie używane podczas omawiania obiektów optycznych, takich jak lustra i soczewki. Każda wypukła powierzchnia będzie wystawać na zewnątrz, podobnie jak bańka, co daje efekt szerokości. Lustra wypukłe są powszechnie spotykane wewnątrz garaży, gdzie kierowcy potrzebują szerokiego widoku wokół zakrętów lub potencjalnych martwych punktów.

W kontraście, wklęsłe lustro jest zakrzywione do wewnątrz i produkuje powiększone odbicie, które jest do góry nogami. Jak pokazała Szkoła Fizyki Uniwersytetu Południowej Walii, każdy, kto ma błyszczącą łyżkę, może sprawdzić tę obserwację, patrząc na swoje odbicie w łyżce. Na wklęsłej powierzchni łyżki, gdzie podnosisz jedzenie, twoje odbicie jest zniekształcone w wąski sposób, a ty wydajesz się być do góry nogami. Ale jeśli odwrócisz swoją łyżkę na wypukłą stronę, twoje odbicie będzie pionowe i mniejsze.

Odbicia różnią się tak bardzo pomiędzy powierzchniami wypukłymi i wklęsłymi, ponieważ czy powierzchnia zakrzywia się na zewnątrz czy do wewnątrz, lustro samo w sobie jest częścią sfery. Ponieważ powierzchnia kuli nie jest płaska, światło odbite od jej powierzchni przebywa różne odległości zanim zetknie się z lustrem.

Zależnie od tego, z którym obszarem powierzchni światło się styka, promień światła może odbijać się od pobliskich powierzchni, tworząc bardziej skupiony obszar widoczności. To dlatego, patrząc na wewnętrzną powierzchnię łyżki, można zobaczyć tylko odbicie tego, co jest najbliżej powierzchni łyżki – nawet jeśli nadal wydaje się ona mniejsza. Ponadto, jeśli umieścimy palec wewnątrz łyżki, powierzchnia lustra może wytworzyć dwa lub trzy różne odbicia w tym samym czasie.

Soczewka wklęsła vs. soczewka wypukła

Soczewki wklęsłe i wypukłe występują w przedmiotach codziennego użytku, takich jak okulary, kontakty, lornetki i teleskopy. Podobnie jak nauka o odbiciu światła w lustrach wypukłych i wklęsłych, istnieją również wzory na to, jak światło przechodzi przez soczewki wklęsłe i wypukłe, aby wytworzyć widoczny obraz.

Soczewki wypukłe

Według Akademii Manocha soczewki wypukłe są nazywane soczewkami zbieżnymi ze względu na ich zdolność do wytwarzania obrazów, które są pomniejszone, powiększone lub introwertyczne. To, jak dokładnie obraz pojawia się przez soczewkę wypukłą, zależy od tego, jak blisko obiektu znajduje się punkt ogniskowy soczewki. Dla każdej soczewki wypukłej istnieją symetryczne punkty ogniskowe po obu stronach soczewki.

To, jak dokładnie obiekt jest wytwarzany przez soczewkę wypukłą, można przewidzieć na podstawie trzech zasad:

Zasada 1: Każdy promień światła przechodzący przez soczewkę wypukłą jest równoległy do osi głównej, która jest linią centralną przechodzącą przez absolutny środek soczewki sferycznej. Gdy światło zetknie się z soczewką, ulega załamaniu i przechodzi przez ognisko po drugiej stronie. Przechodzące promienie światła, które są równoległe do osi głównej, wędrują ponad obiektem znajdującym się przed soczewką.

Zasada 2: Każdy promień światła, który przechodzi przez środek soczewki wypukłej, będzie kontynuowany w linii prostej po drugiej stronie.

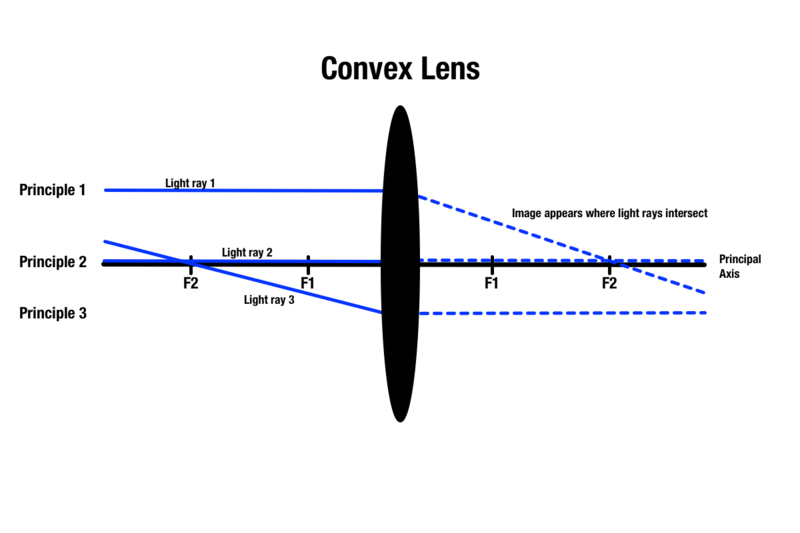
Choć istnieją trzy zasady przewidywania jakości obrazu przez soczewkę wypukłą, podczas rysowania wykresu promieni do obiektu można zastosować tylko dwie zasady. Dowolne dwie zasady spowodują powstanie przecięcia światła po drugiej stronie soczewki, co wskaże obszar, w którym pojawia się obraz obiektu.

Im dalej od soczewki wypukłej znajduje się obiekt, tym mniejszy będzie jego obraz po drugiej stronie, a im bliżej soczewki wypukłej znajduje się obiekt, tym większy będzie się on pojawiał. Obiekt znajdujący się poza najbliższym punktem ogniskowym daje większy obraz za nim. Jak zauważa Akademia Manocha, ten typ powiększenia soczewki jest używany w narzędziach optycznych, takich jak szkła powiększające.

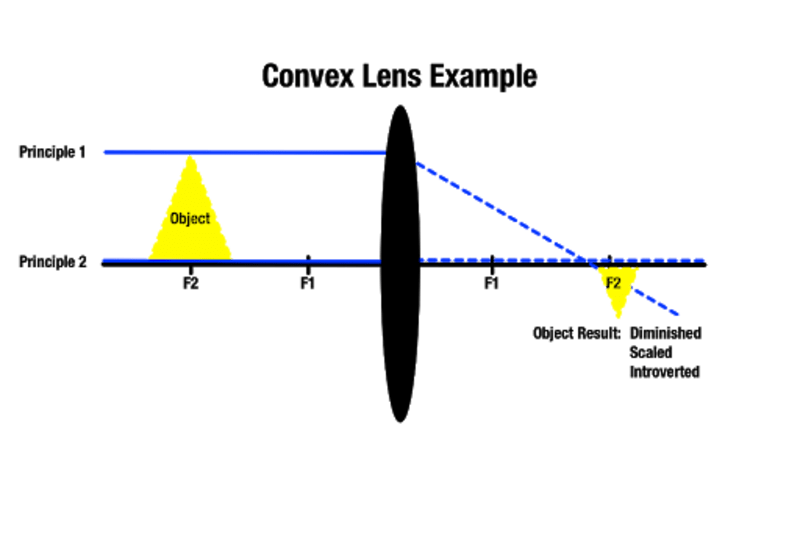
Zależnie od tego, w którym punkcie ogniskowym znajduje się obiekt, możliwe jest uzyskanie obrazu o przybliżonym rozmiarze. Możliwe jest również tworzenie prawdziwych obrazów, które nie są widoczne, jeśli przechodzące promienie światła nigdy się nie przecinają, ponieważ są równoległe po drugiej stronie. W tym przypadku wytworzony obraz istnieje w nieskończonej odległości.

Soczewki wklęsłe

Każda soczewka wklęsła będzie miała grubszą średnicę, a cieńszy środek, ponieważ soczewka wklęsła jest zakrzywiona do wewnątrz. Kształt soczewek wklęsłych pozwala światłu rozproszyć się po zetknięciu z soczewką, co pozwala wirtualnym obiektom wydawać się mniejszymi. Zdolność soczewki wklęsłej do rozpraszania światła sprawia, że jest to idealna soczewka dla narzędzi takich jak latarki, gdzie centralne źródło światła może być używane na większej powierzchni.

Soczewki wklęsłe generują obrazy z trzema zasadami, które są podobne do zasad działania soczewek wypukłych:

Zasada 1: Każdy promień światła poruszający się nad obiektem i równoległy do osi głównej załamuje się po zetknięciu z soczewką i wygląda tak, jakby pochodził z kierunku najbliższego ogniska.

Zasada 2: Każdy promień światła przechodzący przez środek soczewki wklęsłej przejdzie przez nią bez załamania.
Zasada 3: Każdy promień światła skierowany w stronę ogniska po drugiej stronie soczewki wklęsłej załamuje się i staje się równoległy do osi głównej.

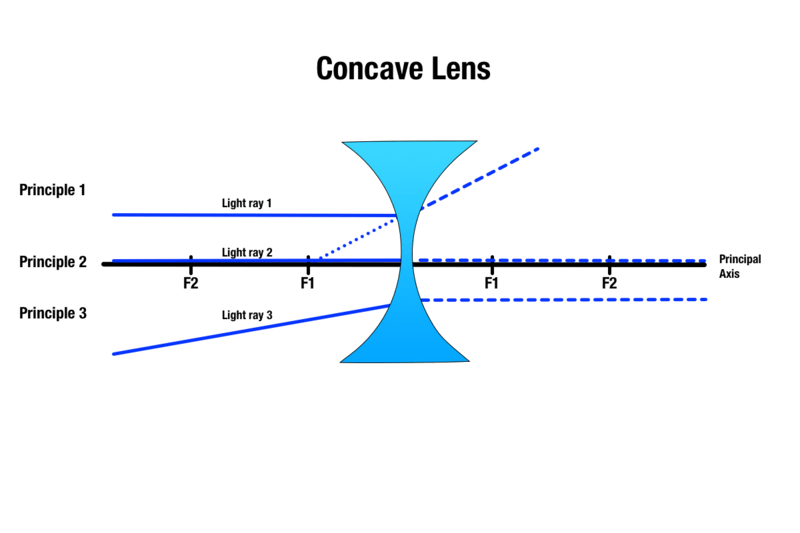
Pomimo że rozmiar obrazu obiektu będzie się różnił w zależności od odległości obiektu od soczewki wklęsłej, wytworzony obraz jest zawsze wirtualny, pionowy, mniejszy i pojawia się po tej samej stronie soczewki co obiekt.

Wklęsły vs. wypukły w piśmie

Słowa wklęsły i wypukły są sobie przeciwstawne i zasadniczo opisują kształt przedmiotów lub powierzchni w ten sam sposób, w jaki przeciwstawiamy sobie słowa takie jak:

• Mały vs. big
• Tall vs. short
• Slim vs. wide
• Round vs. flat

Because concave and convex are technical words, using them descriptively for prose can produce a more metaphorical or abstract interpretation for casual audiences. Oznacza to, że jeśli pisarze zdecydują się użyć wklęsłości lub wypukłości poza sferą ich typowego użycia, pisarz musi zdecydować, jak jasne ma być ich pismo.

Rozważmy przymiotnik

Znakomitym przykładem użycia wklęsłości lub wypukłości w literaturze jest rozważenie pism amerykańskiego autora Davida Fostera Wallace’a (lub DFW w skrócie). DFW jest znany ze swojego złożonego i technicznego stylu pisania – i tak, użył wklęsłości i wypukłości do opisania rzeczowników kilka razy. Wallace używa wklęsłości i wypukłości w następujących przykładach:

„Moje oko było w porządku, ale nie byłem ani duży, ani szybki, miałem prawie wklęsłą klatkę piersiową i nadgarstki tak cienkie, że mogłem je usztywnić kciukiem i palcem…”

– „Tennis, Trigonometry, Tornados: A Midwestern Boyhood”, Harper’s Magazine.

„…oczy lalki, które otwierają się z pociągnięciem struny serca, wklęsłe tam, gdzie ja jestem wypukły.”

– „Order and Flux in Northampton,” Conjunctions.

Punktem użycia przykładów DFW nie jest tylko pokazanie, jak pisarze użyli convex lub concave poza kontekstem matematycznym, ale raczej, dla pisarzy do rozważenia, czy użycie technicznych lub abstrakcyjnych terminów jest pomocne dla jasnego komunikowania się z ich publicznością.
W pierwszym przykładzie DFW, użycie wklęsłości ma sens, ponieważ opisuje on strukturę czegoś. Ale, używając wklęsłości i wypukłości do opisania nieobiektywnych rzeczowników, takich jak uczucia lub myśli, ma tendencję do zaciemniania znaczenia tego, co próbujemy wyjaśnić. Drugi przykład DFW idzie po cienkiej linii podczas używania wklęsłości i wypukłości, ponieważ ich użycie jest zarówno dosłowne jak i metaforyczne.

FAQ: Related terms

What is a function?

A function is the equation of a line on a graph. Funkcje są różne dla każdej linii na wykresie, ale przyjmują ogólną postać,

f(x) = x + 1

W przypadku każdej funkcji liniowej zmienną zależną jest zazwyczaj f(x), a każda nieznana zmienna w funkcji jest nazywana zmienną niezależną.

Co to jest dziedzina?

Działka to zbiór zmiennych niezależnych na wykresie, który odpowiada funkcji linii. Domeny są ważne do zrozumienia, ponieważ lokalizują konkretne punkty na wykresie, który odpowiada każdemu rzeczywistemu wyjściu równania.

Co to jest przedział?

Zakres dowolnej funkcji reprezentuje każdą możliwą wartość wzdłuż osi x lub y na wykresie, która daje ważną wartość dla zmiennej zależnej. Wszystkie minimalne i maksymalne liczby całkowite są identyfikowane przez zastąpienie zmiennych na osi x lub y.

Co to jest przedział?

Przedział jest zbiorem liczb, które reprezentują liczby całkowite linii, aka dziedzinę. Zamknięty przedział zawiera dwa skończone punkty linii, gdzie linia nie istnieje już poza zakresem liczby całkowitej. Otwarty przedział to zbiór liczb całkowitych, które nie reprezentują absolutnego końca domeny linii.

Sprawdź się!

Sprawdź, jak dobrze rozumiesz różnicę między wypukłością i wklęsłością za pomocą następujących pytań wielokrotnego wyboru:

1. Patrząc na błyszczącą łyżkę, zauważasz, że twoje odbicie jest do góry nogami. Powierzchnia łyżki jest powierzchnią _________.
   a. Wypukła
   b. Lustrzana
   c. Wklęsła
   d. Metalowa
2. Z punktu widzenia wykresów funkcji, funkcją wypukłą nazywa się czasem:
   a. Wklęsła do góry
   b. Wypukła w dół
   c. Wklęsła do dołu
   d. A i B
3. Które z poniższych stwierdzeń nie opisuje powierzchni wklęsłej:
   a. Wydrążona półkula
   b. Soczewka do oczu
   c. Miska na płatki zbożowe
   d. Półkula
4. Które z poniższych określeń nie opisuje powierzchni wypukłej:
   a. Postać Stewie z serialu Family Guy
   b. Sfera
   c. Lustro na parkingu
   d. Piłka nożna
5. Który z poniższych kształtów nie może istnieć jako wielokąt wklęsły:
   a. Pięciokąt
   b. Sześciokąt
   c. Trójkąt
   d. Octagon

Answers

1. C: Concave
2. D: A i B
3. D: Hemisphere
4. B: Sphere
5. C: Triangle

Źródła:

1. Bourne, M. „Domain and Range of a Function.” Interactive Mathematics, Jan. 4, 2019.
2. „Concave.” Merriam-Webster Dictionary, 2019.
3. „Concave.” The Oxford Dictionary of Word Histories, Ed. Chantrell, 2002, s. 110.
4. „Concave and Convex Mirrors.” Akademia Manocha, YouTube, 2019.
5. „Soczewki wklęsłe: Definition & Uses.” Study.com, 2019.
6. „Convex.” Merriam-Webster Dictionary, 2019.
7. „Convex and Concave Lenses.” Manocha Academy, YouTube, 2019.
8. „Mathematics / Understanding Polygons.” Learnhive Inc, 2018.
9. „Odbicie od lustra wklęsłego.” UNSW Physics, YouTube, 2017.
10. Wallace, D.F. „Tennis, Trigonometry, Tornadoes: A Midwestern Boyhood.” Harper’s Magazine, 1991.
11. Wallace, D.F. „Order and Flux in Northampton.” Conjunctions, 1991.
12. Weisstein, Eric W. „Concave Function.” MathWorld-A Wolfram Web Resource, n.d.
13. Weisstein, Eric W. „Convex Function.” MathWorld-A Wolfram Web Resource, n.d.

The Word Counter jest dynamicznym narzędziem online używanym do liczenia słów, znaków, zdań, akapitów i stron w czasie rzeczywistym, wraz ze sprawdzaniem pisowni i gramatyki.

.