Gdy dane są gotowe do analizy, należy dokładnie ocenić, na podstawie inspekcji danych, czy metody statystyczne powinny być stosowane do obsługi brakujących danych. Bell i wsp. mieli na celu ocenę zakresu i sposobu postępowania z brakującymi danymi w randomizowanych badaniach klinicznych opublikowanych między lipcem a grudniem 2013 r. w BMJ, JAMA, Lancet i New England Journal of Medicine . 95% z 77 zidentyfikowanych prób zgłaszało pewne brakujące dane dotyczące wyników. Najczęściej stosowaną metodą obsługi brakujących danych w analizie pierwotnej była kompletna analiza przypadku (45%), pojedyncza imputacja (27%), metody oparte na modelu (na przykład modele mieszane lub uogólnione równania szacunkowe) (19%) i wielokrotna imputacja (8%) .
Kompletna analiza przypadku
Kompletna analiza przypadku jest analizą statystyczną opartą na uczestnikach z kompletnym zestawem danych wynikowych. Uczestnicy z jakimikolwiek brakującymi danymi są wyłączani z analizy. Jak opisano we wstępie, jeśli brakujące dane są MCAR, analiza kompletnych przypadków będzie miała zmniejszoną moc statystyczną ze względu na zmniejszoną wielkość próby, ale obserwowane dane nie będą tendencyjne. Jeżeli brakujące dane nie są MCAR, oszacowanie efektu interwencji na podstawie kompletnej analizy przypadku może być oparte, tzn. często będzie istniało ryzyko przeszacowania korzyści i niedoszacowania szkód. Proszę zapoznać się z sekcją „Should multiple imputation be used to handle missing data?” w celu bardziej szczegółowego omówienia potencjalnej ważności w przypadku zastosowania analizy kompletnego przypadku.
Single imputation
W przypadku zastosowania imputacji pojedynczej, brakujące wartości są zastępowane wartością określoną przez pewną regułę . Istnieje wiele form pojedynczej imputacji, na przykład ostatnia obserwacja przeniesiona do przodu (brakujące wartości uczestnika są zastępowane przez ostatnią zaobserwowaną wartość uczestnika), najgorsza obserwacja przeniesiona do przodu (brakujące wartości uczestnika są zastępowane przez najgorszą zaobserwowaną wartość uczestnika) i prosta imputacja średnia. W prostej imputacji średniej, brakujące wartości są zastępowane przez średnią dla tej zmiennej. Stosowanie pojedynczej imputacji często prowadzi do niedoszacowania zmienności, ponieważ każda nieobserwowana wartość ma taką samą wagę w analizie jak znane, obserwowane wartości. Ważność pojedynczej imputacji nie zależy od tego, czy dane są MCAR; pojedyncza imputacja zależy raczej od określonych założeń, że brakujące wartości, na przykład, są identyczne z ostatnią obserwowaną wartością. Te założenia są często nierealistyczne i dlatego pojedyncza imputacja jest często potencjalnie stronniczą metodą i powinna być stosowana z dużą ostrożnością.
Wielokrotna imputacja
Wielokrotna imputacja okazała się być ważną ogólną metodą radzenia sobie z brakującymi danymi w randomizowanych badaniach klinicznych, a metoda ta jest dostępna dla większości typów danych. W następnych sekcjach opiszemy, kiedy i jak należy stosować imputację wielokrotną.
Czy imputacja wielokrotna powinna być stosowana do obsługi brakujących danych?
Powody, dla których imputacja wielokrotna nie powinna być stosowana do obsługi brakujących danych
Czy ważne jest ignorowanie brakujących danych?
Analiza danych obserwowanych (analiza kompletnych przypadków) ignorująca brakujące dane jest ważnym rozwiązaniem w trzech okolicznościach.
- a)
Analiza kompletnych przypadków może być stosowana jako analiza pierwotna, jeśli odsetek brakujących danych jest mniejszy niż około 5% (jako zasada kciuka) i nie jest prawdopodobne, że pewne grupy pacjentów (na przykład bardzo chorzy lub bardzo „zdrowi” uczestnicy) są szczególnie utracone na rzecz obserwacji w jednej z porównywanych grup. Innymi słowy, jeśli potencjalny wpływ brakujących danych jest nieistotny, wówczas brakujące dane mogą być pominięte w analizie. W razie wątpliwości można zastosować analizy wrażliwości dla najlepszego i najgorszego przypadku: najpierw generowany jest zbiór danych scenariusza „najlepszy-najgorszy przypadek”, w którym zakłada się, że wszyscy uczestnicy utraceni w obserwacji w jednej grupie (zwanej grupą 1) mieli korzystny wynik (na przykład nie mieli poważnego zdarzenia niepożądanego), a wszyscy z brakującymi wynikami w drugiej grupie (grupa 2) mieli szkodliwy wynik (na przykład mieli poważne zdarzenie niepożądane) . Następnie generowany jest zbiór danych scenariusza „najgorszy-najlepszy przypadek”, w którym zakłada się, że wszyscy uczestnicy utraceni w obserwacji w grupie 1 mieli szkodliwy wynik, a wszyscy utraceni w obserwacji w grupie 2 mieli korzystny wynik. Jeżeli stosowane są wyniki ciągłe, wówczas „korzystny wynik” może być średnią grupy plus 2 odchylenia standardowe (lub 1 odchylenie standardowe) średniej grupy, a „szkodliwy wynik” może być średnią grupy minus 2 odchylenia standardowe (lub 1 odchylenie standardowe) średniej grupy. Dla danych dychotomizowanych, te analizy wrażliwości dla najlepszego i najgorszego przypadku pokażą zakres niepewności z powodu brakujących danych, i jeśli ten zakres nie daje jakościowo sprzecznych wyników, wtedy brakujące dane mogą być pominięte. Dla danych ciągłych imputacja z 2 SD będzie reprezentować możliwy zakres niepewności biorąc pod uwagę 95% obserwowanych danych (jeśli są one normalnie rozłożone).
- b)
Jeśli tylko zmienna zależna ma brakujące wartości i zmienne pomocnicze (zmienne nie włączone do analizy regresji, ale skorelowane ze zmienną z brakującymi wartościami i/lub związane z jej brakiem) nie są zidentyfikowane, analiza kompletnego przypadku może być użyta jako analiza pierwotna i nie należy stosować żadnych szczególnych metod do obsługi brakujących danych. Nie uzyska się żadnych dodatkowych informacji poprzez, na przykład, zastosowanie wielokrotnej imputacji, ale błędy standardowe mogą wzrosnąć ze względu na niepewność wprowadzoną przez wielokrotną imputację .
- c)
Jak wspomniano powyżej (patrz Metody postępowania z brakującymi danymi), ważne byłoby również przeprowadzenie kompletnej analizy przypadku, jeżeli jest względnie pewne, że dane są MCAR (patrz Wprowadzenie). Stosunkowo rzadko zdarza się, że jest pewne, że dane są MCAR. Możliwe jest przetestowanie hipotezy, że dane są MCAR za pomocą testu Little’a, ale nierozsądne może być opieranie się na testach, które okazały się nieistotne. W związku z tym, jeśli istnieją uzasadnione wątpliwości, czy dane są MCAR, nawet jeśli test Little’a jest nieistotny (nie udaje się odrzucić hipotezy zerowej, że dane są MCAR), nie należy zakładać MCAR.
Czy proporcje brakujących danych są zbyt duże?
Jeśli brakuje dużych proporcji danych, należy rozważyć jedynie przekazanie wyników kompletnej analizy przypadku, a następnie wyraźnie omówić wynikające z tego ograniczenia interpretacyjne wyników badania. Jeśli wielokrotna imputacja lub inne metody są stosowane do obsługi brakujących danych, może to wskazywać, że wyniki badania są potwierdzające, co nie jest prawdą, jeśli brak danych jest znaczny. Jeżeli proporcje brakujących danych są bardzo duże (np. ponad 40%) w odniesieniu do ważnych zmiennych, wówczas wyniki badania mogą być traktowane jedynie jako wyniki generujące hipotezę. Rzadki wyjątek stanowi sytuacja, w której mechanizm leżący u podstaw brakujących danych można opisać jako MCAR (patrz akapit powyżej).
Czy zarówno założenie MCAR, jak i MAR wydają się niewiarygodne?
Jeśli założenie MAR wydaje się niewiarygodne w oparciu o charakterystykę brakujących danych, wówczas wyniki badania będą narażone na ryzyko tendencyjnych wyników z powodu „tendencyjności niekompletnych danych dotyczących wyników”, a żadna metoda statystyczna nie może z pewnością uwzględnić tej potencjalnej tendencyjności. Prawidłowość metod stosowanych do obsługi danych MNAR wymaga pewnych założeń, których nie można przetestować w oparciu o obserwowane dane. Analizy wrażliwości dla najlepszego i najgorszego przypadku mogą wykazać pełen teoretyczny zakres niepewności, a wnioski powinny być odnoszone do tego zakresu niepewności. Ograniczenia analiz powinny być dokładnie przedyskutowane i rozważone.
Czy zmienna wynikowa z brakującymi wartościami jest ciągła i czy model analityczny jest skomplikowany (np. z interakcjami)?
W tej sytuacji można rozważyć zastosowanie bezpośredniej metody największej wiarygodności, aby uniknąć problemów zgodności modelu między modelem analitycznym a modelem wielokrotnej imputacji, gdzie pierwszy jest bardziej ogólny niż drugi. Ogólnie, bezpośrednie metody największej wiarygodności mogą być używane, ale według naszej wiedzy komercyjnie dostępne metody są obecnie dostępne tylko dla zmiennych ciągłych.
Kiedy i jak używać wielokrotnej imputacji
Jeśli żaden z „Powodów, dla których wielokrotna imputacja nie powinna być używana do obsługi brakujących danych” z powyżej jest spełniony, wtedy wielokrotna imputacja może być użyta. Różne procedury zostały zaproponowane w literaturze w ciągu ostatnich kilku dekad, aby poradzić sobie z brakującymi danymi. Powyższe rozważania na temat metod statystycznych do obsługi brakujących danych przedstawiliśmy na Rys. 1.
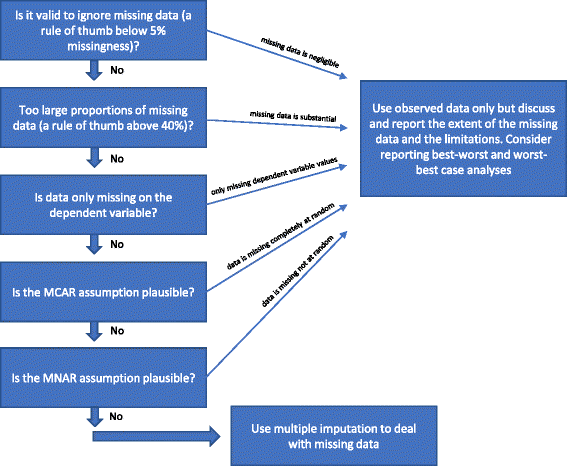
Flowchart: when should multiple imputation be used to handle missing data when analysing results of randomised clinical trials
Multiple imputation originated in the early 1970s, and has gained increasing popularity over the years . Wielokrotna imputacja jest opartą na symulacji techniką statystyczną do obsługi brakujących danych. Imputacja wielokrotna składa się z trzech kroków:
-
Krok imputacji. Imputacja” zasadniczo reprezentuje jeden zestaw prawdopodobnych wartości dla brakujących danych – imputacja wielokrotna reprezentuje wiele zestawów prawdopodobnych wartości. Przy imputacji wielokrotnej brakujące wartości są identyfikowane i zastępowane losową próbką imputacji prawdopodobnych wartości (uzupełnione zbiory danych). Wielokrotne uzupełnione zbiory danych są generowane poprzez pewien wybrany model imputacji. Pięć imputowanych zbiorów danych było tradycyjnie sugerowane jako wystarczające na gruncie teoretycznym, ale 50 zbiorów danych (lub więcej) wydaje się być preferowane w celu zmniejszenia zmienności próbkowania z procesu imputacji .
-
Krok analizy (estymacji) danych uzupełnionych. Pożądana analiza jest wykonywana oddzielnie dla każdego zbioru danych, który jest generowany podczas etapu imputacji. W ten sposób konstruuje się np. 50 wyników analizy.
-
Krok łączenia danych. Wyniki uzyskane z każdej zakończonej analizy danych są łączone w jeden wynik wielokrotnej imputacji . Nie ma potrzeby przeprowadzania metaanalizy ważonej, ponieważ wszystkie powiedzmy 50 wyników analiz uważa się za mające tę samą wagę statystyczną.
Ważne jest, aby istniała albo zgodność między modelem imputacji a modelem analizy, albo model imputacji jest bardziej ogólny niż model analizy (na przykład, że model imputacji obejmuje więcej niezależnych zmiennych niż model analizy) . Na przykład, jeśli model analizy ma znaczące interakcje, to model imputacji powinien je również zawierać, jeśli model analizy używa przekształconej wersji zmiennej, to model imputacji powinien używać tego samego przekształcenia, itd. Przedstawimy je zgodnie z ich rosnącym stopniem złożoności: 1) analiza regresji jednowartościowej; 2) imputacja monotoniczna; 3) równania łańcuchowe lub metoda łańcucha Markowa Monte Carlo (MCMC). W kolejnych punktach opiszemy te różne metody imputacji wielokrotnej i sposób wyboru między nimi.
Jednowartościowa analiza regresji obejmuje zmienną zależną i zmienne stratyfikacyjne używane w randomizacji. Zmienne stratyfikacyjne często zawierają wskaźnik ośrodka, jeśli badanie jest badaniem wieloośrodkowym i zwykle jedną lub więcej zmiennych korygujących z informacjami prognostycznymi, które są skorelowane z wynikiem. Kiedy używana jest ciągła zmienna zależna, może być również uwzględniona wartość początkowa zmiennej zależnej. Jak wspomniano w części „Powody, dla których nie należy stosować metod statystycznych do obsługi brakujących danych”, jeżeli tylko zmienna zależna ma brakujące wartości, a zmienne pomocnicze nie zostały zidentyfikowane, należy przeprowadzić pełną analizę przypadku i nie należy stosować żadnych szczególnych metod do obsługi brakujących danych. Jeżeli zmienne pomocnicze zostały zidentyfikowane, można przeprowadzić imputację pojedynczej zmiennej. Jeśli występują znaczne braki w zmiennej wyjściowej zmiennej ciągłej, pełna analiza przypadku może dostarczyć tendencyjnych wyników. Dlatego we wszystkich przypadkach imputacja pojedynczej zmiennej (z lub bez zmiennych pomocniczych włączonych odpowiednio) jest przeprowadzana, jeśli brakuje tylko zmiennej linii podstawowej.
Jeśli zarówno zmienna zależna, jak i zmienna linii podstawowej są brakujące, a brak jest monotoniczny, wykonuje się imputację monotoniczną. Przyjmijmy macierz danych, w której pacjenci są reprezentowani przez wiersze, a zmienne przez kolumny. Brak w takiej macierzy danych jest monotoniczny, jeśli jej kolumny mogą być uporządkowane w taki sposób, że dla każdego pacjenta (a) jeśli brakuje wartości, brakuje również wszystkich wartości na prawo od tej pozycji i (b) jeśli wartość jest obserwowana, wszystkie wartości na lewo od tej wartości są również obserwowane. Jeśli brak wartości jest monotoniczny, metoda wielokrotnej imputacji jest również stosunkowo prosta, nawet jeśli więcej niż jedna zmienna ma brakujące wartości. W tym przypadku stosunkowo proste jest imputowanie brakujących danych przy użyciu sekwencyjnej imputacji regresji, gdzie brakujące wartości są imputowane dla każdej zmiennej na raz . Wiele pakietów statystycznych (na przykład STATA) może analizować, czy brak jest monotoniczny czy nie.
Jeśli brak nie jest monotoniczny, wielokrotna imputacja jest przeprowadzana przy użyciu równań łańcuchowych lub metody MCMC. Zmienne pomocnicze są włączane do modelu, jeśli są dostępne. Podsumowaliśmy, jak wybrać między różnymi metodami imputacji wielokrotnej na Rys. 2.
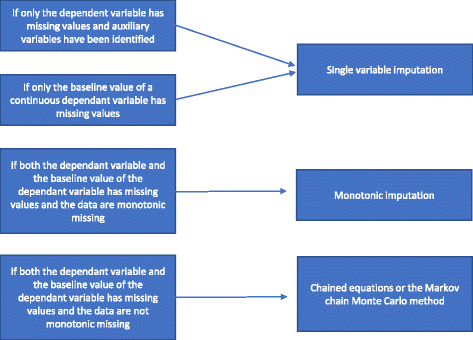
Flowchart of multiple imputation
Full information maximum likelihood
Full information maximum likelihood jest alternatywną metodą radzenia sobie z brakującymi danymi . Zasada estymacji maksymalnej wiarygodności polega na oszacowaniu parametrów wspólnego rozkładu wyniku (Y) i zmiennych (X1,…, Xk), które, jeśli są prawdziwe, zmaksymalizowałyby prawdopodobieństwo zaobserwowania wartości, które w rzeczywistości zaobserwowaliśmy. Jeśli brakuje wartości u danego pacjenta, możemy uzyskać prawdopodobieństwo poprzez zsumowanie zwykłego prawdopodobieństwa nad wszystkimi możliwymi wartościami brakujących danych, pod warunkiem, że mechanizm brakujących danych jest ignorowalny. Metoda ta jest określana mianem maksymalnego prawdopodobieństwa z pełną informacją .
Pełna informacja maksymalna prawdopodobieństwo ma zarówno mocne strony, jak i ograniczenia w porównaniu z imputacją wielokrotną.
Mocne strony pełnej informacji maksymalna prawdopodobieństwo w porównaniu z imputacją wielokrotną
- 1)
Jest prostsza do wdrożenia, tj. nie jest konieczne przechodzenie przez różne kroki, jak w przypadku imputacji wielokrotnej.
- 2)
W przeciwieństwie do imputacji wielokrotnej, pełna informacja największej wiarygodności nie ma potencjalnych problemów z niezgodnością między modelem imputacji a modelem analizy (patrz „Imputacja wielokrotna”). Ważność wyników imputacji wielokrotnej będzie wątpliwa, jeśli istnieje niezgodność między modelem imputacji a modelem analizy lub jeśli model imputacji jest mniej ogólny niż model analizy .
- 3)
W przypadku stosowania imputacji wielokrotnej wszystkie brakujące wartości w każdym wygenerowanym zbiorze danych (krok imputacji) są zastępowane losową próbką prawdopodobnych wartości . W związku z tym, o ile nie określono „losowego materiału siewnego”, za każdym razem, gdy przeprowadzana jest analiza imputacji wielokrotnej, wyświetlane będą różne wyniki. Analizy przy użyciu maksymalnego prawdopodobieństwa pełnej informacji na tym samym zbiorze danych dadzą te same wyniki za każdym razem, gdy analiza jest wykonywana, a zatem wyniki nie są zależne od losowego ziarna. Jednakże, jeśli wartość losowego ziarna jest zdefiniowana w planie analizy statystycznej, problem ten może zostać rozwiązany.
Ograniczenia pełnej informacji maksymalnego prawdopodobieństwa w porównaniu z wielokrotną imputacją
Ograniczenia użycia pełnej informacji maksymalnego prawdopodobieństwa w porównaniu z użyciem wielokrotnej imputacji, jest to, że użycie pełnej informacji maksymalnego prawdopodobieństwa jest możliwe tylko przy użyciu specjalnie zaprojektowanego oprogramowania . Zaprojektowane wstępne oprogramowanie zostało opracowane, ale większość z nich nie posiada cech komercyjnego oprogramowania statystycznego (na przykład STATA, SAS lub SPSS). W STATA (przy użyciu polecenia SEM) i SAS (przy użyciu polecenia PROC CALIS) możliwe jest zastosowanie maksymalnego prawdopodobieństwa z pełną informacją, ale tylko w przypadku stosowania ciągłych zmiennych zależnych (wynikowych). W przypadku regresji logistycznej i regresji Coxa jedynym komercyjnym pakietem, który zapewnia pełną informację o maksymalnej wiarygodności dla brakujących danych, jest Mplus.
Kolejnym potencjalnym ograniczeniem przy stosowaniu pełnej informacji o maksymalnej wiarygodności jest to, że u podstaw może leżeć założenie normalności wielowymiarowej. Niemniej jednak, naruszenia założeń normalności wieloczynnikowej mogą nie być tak ważne, więc może być dopuszczalne włączenie binarnych zmiennych niezależnych do analizy.
W pliku dodatkowym 1 zamieściliśmy program (SAS), który produkuje pełny zestaw danych zabawek, w tym kilka różnych analiz tych danych. Tabela 1 i Tabela 2 pokazują dane wyjściowe i to, jak różne metody, które obsługują brakujące dane, dają różne wyniki.
Analiza regresji wartości panelu
Dane panelu są zwykle zawarte w tak zwanym szerokim pliku danych, w którym pierwszy wiersz zawiera nazwy zmiennych, a kolejne wiersze (jeden dla każdego pacjenta) zawierają odpowiadające im wartości. Wynik jest reprezentowany przez różne zmienne – po jednej dla każdego zaplanowanego, czasowego pomiaru wyniku. Aby przeanalizować dane, należy przekonwertować plik na tak zwany długi plik z jednym rekordem na planowany pomiar wyniku, zawierający wartość wyniku, czas pomiaru i kopię wszystkich innych wartości zmiennych z wyjątkiem wartości zmiennej wyniku. Aby zachować wewnątrzpacjenckie korelacje pomiędzy czasowymi pomiarami wyników, powszechną praktyką jest wykonanie wielokrotnej imputacji pliku danych w jego szerokiej formie, a następnie analiza pliku wynikowego po przekształceniu go w jego długą formę. Proc mixed (SAS 9.4) może być użyty do analizy ciągłych wartości wyników, a proc. glimmix (SAS 9.4) do innych typów wyników. Ponieważ procedury te stosują bezpośrednią metodę największej wiarygodności na danych wynikowych, ale ignorują przypadki z brakującymi wartościami zmiennych, procedury te mogą być stosowane bezpośrednio, gdy brakuje tylko wartości zmiennej zależnej i nie są dostępne dobre zmienne pomocnicze. W przeciwnym razie należy zastosować proc. mixed lub proc. glimmix (w zależności od tego, który z nich jest właściwy) po przeprowadzeniu wielokrotnych obliczeń. Oczywiście, analogiczne podejście może być możliwe przy użyciu innych pakietów statystycznych.
Analizy wrażliwości
Analizy wrażliwości mogą być zdefiniowane jako zestaw analiz, w których dane są traktowane w inny sposób w porównaniu do analizy pierwotnej. Analizy wrażliwości mogą pokazać, w jaki sposób założenia inne niż przyjęte w analizie pierwotnej wpływają na uzyskane wyniki. Analiza wrażliwości powinna być wstępnie zdefiniowana i opisana w planie analizy statystycznej, ale dodatkowe analizy wrażliwości post hoc mogą być uzasadnione i ważne. Gdy potencjalny wpływ brakujących wartości jest niejasny, zalecamy następujące analizy wrażliwości:
-
Opisaliśmy już wykorzystanie analiz wrażliwości best-worst i worst-best case w celu pokazania zakresu niepewności z powodu brakujących danych (patrz Ocena, czy metody powinny być stosowane do obsługi brakujących danych). Nasz poprzedni opis analiz wrażliwości dla najlepszego i najgorszego przypadku odnosił się do brakujących danych dla dychotomicznej lub ciągłej zmiennej zależnej, ale te analizy wrażliwości mogą być również stosowane w przypadku braku danych dla zmiennych stratyfikacyjnych, wartości początkowych itp. Potencjalny wpływ brakujących danych powinien być oceniany dla każdej zmiennej oddzielnie, tj. powinien istnieć jeden najlepszy najgorszy i jeden najgorszy najlepszy scenariusz dla każdej zmiennej (zmienna zależna, wskaźnik wyniku i zmienne stratyfikacyjne) z brakującymi danymi.
-
Jeśli zostanie podjęta decyzja, że np. należy zastosować wielokrotną imputację, to wyniki te powinny być pierwotnym wynikiem danego wyniku. Każda pierwotna analiza regresji powinna być zawsze uzupełniona o odpowiadającą jej analizę obserwowanych (lub dostępnych) przypadków.
Gdy stosowane są metody z efektem mieszanym
Użycie wieloośrodkowego projektu badania będzie często konieczne, aby zrekrutować wystarczającą liczbę uczestników badania w rozsądnych ramach czasowych. Projekt badania wieloośrodkowego stanowi również lepszą podstawę dla późniejszego uogólnienia jego wyników. Wykazano, że najczęściej stosowane metody analizy w randomizowanych badaniach klinicznych sprawdzają się dobrze przy małej liczbie ośrodków (analiza wyników zależnych od czynników binarnych). Przy stosunkowo dużej liczbie ośrodków (50 lub więcej) często optymalne jest użycie „ośrodka” jako efektu losowego i zastosowanie metod analizy efektów mieszanych. Często ważne jest również stosowanie metod analizy efektów mieszanych przy analizie danych podłużnych. W niektórych okolicznościach ważne może być włączenie zmiennej „efekt losowy” (na przykład „centrum”) jako zmiennej o stałym efekcie podczas etapu imputacji, a następnie zastosowanie analizy modelu mieszanego lub uogólnionych równań estymacyjnych (GEE) podczas etapu analizy . Jednakże zastosowanie modelu mieszanych efektów (z, na przykład, „centrum” jako efektem losowym) oznacza, że wielowarstwowa struktura danych musi być brana pod uwagę przy modelowaniu wielokrotnej imputacji. Obecnie, komercyjne oprogramowanie nie jest bezpośrednio dostępne, aby to zrobić. Można jednak skorzystać z pakietu REALCOME, który może być połączony z STATA . Interfejs eksportuje dane z brakującymi wartościami ze STATA do REALCOME, gdzie imputacja jest wykonywana z uwzględnieniem wielopoziomowej natury danych i przy użyciu metody MCMC, która obejmuje zmienne ciągłe, a poprzez zastosowanie modelu normalnego ukrytego pozwala również na właściwą obsługę danych dyskretnych. Imputowane zestawy danych mogą być następnie analizowane przy użyciu polecenia STATA „mi estimate:”, które może być połączone z oświadczeniem „mixed” (dla wyniku ciągłego) lub oświadczeniem „meqrlogit” dla wyniku binarnego lub porządkowego w STATA . W analizie danych panelowych można jednak łatwo znaleźć się w sytuacji, w której dane obejmują trzy lub więcej poziomów, na przykład pomiary w obrębie tego samego pacjenta (poziom-1), pacjentów w obrębie ośrodków (poziom-2) i ośrodków (poziom-3). Aby nie angażować się w dość skomplikowany model, który może prowadzić do braku zbieżności lub niestabilnych błędów standardowych i dla którego nie jest dostępne komercyjne oprogramowanie, zalecalibyśmy albo traktowanie efektu centrum jako stałego (bezpośrednio lub po połączeniu małych ośrodków w jeden lub więcej ośrodków o odpowiedniej wielkości, przy użyciu procedury, która musi być określona w planie analizy statystycznej) lub wykluczenie centrum jako zmiennej. Jeśli randomizacja została rozwarstwiona według ośrodka, to drugie podejście doprowadzi do skośności w górę błędów standardowych, co spowoduje nieco konserwatywną procedurę testową .
.