Ostatnio mój kolega zadał mi kilka pytań typu „dlaczego mamy tak wiele funkcji aktywacji?”, „dlaczego jedna działa lepiej niż druga?”, „skąd wiemy, której z nich użyć?”, „czy to twarda matematyka?” i tak dalej. Pomyślałem więc, dlaczego nie napisać artykułu na ten temat dla tych, którzy są zaznajomieni z siecią neuronową tylko na poziomie podstawowym i dlatego zastanawiają się nad funkcjami aktywacji i ich „dlaczego jak-matematyka!”.
UWAGA: Ten artykuł zakłada, że masz podstawową wiedzę o sztucznym „neuronie”. Zalecam zapoznanie się z podstawami sieci neuronowych przed przeczytaniem tego artykułu dla lepszego zrozumienia.
Funkcje aktywacji
Co więc robi sztuczny neuron? Najprościej mówiąc, oblicza „sumę ważoną” swoich danych wejściowych, dodaje uprzedzenie, a następnie decyduje, czy powinien zostać „odpalony”, czy nie (tak, funkcja aktywacji to robi, ale pójdźmy z prądem przez chwilę).
Więc rozważmy neuron.
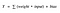
Teraz, wartość Y może być czymkolwiek z zakresu od -inf do +inf. Neuron tak naprawdę nie zna granic tej wartości. Więc jak zdecydujemy, czy neuron powinien się zapalić czy nie (dlaczego taki wzorzec odpalania? Ponieważ nauczyliśmy się tego z biologii, że tak właśnie działa mózg, a mózg jest działającym świadectwem niesamowitego i inteligentnego systemu).
W tym celu postanowiliśmy dodać „funkcje aktywacji”. Aby sprawdzić wartość Y wytwarzaną przez neuron i zdecydować, czy zewnętrzne połączenia powinny uznać ten neuron za „odpalony” czy nie. Albo raczej powiedzmy – „aktywowany” lub nie.
Funkcja krokowa
Pierwszą rzeczą, która przychodzi nam do głowy, jest to, co powiesz na funkcję aktywacji opartą na progu? Jeśli wartość Y jest powyżej pewnej wartości, zadeklaruj ją jako aktywowaną. Jeśli jest mniejsza niż próg, to powiedz, że nie jest. Hmm świetnie. To może zadziałać!
Funkcja aktywacji A = „aktywowana” jeśli Y > próg else nie
Alternatywnie, A = 1 jeśli y> próg, 0 w przeciwnym razie
Cóż, to co właśnie zrobiliśmy jest „funkcją krokową”, zobacz poniższy rysunek.
Jej wyjście wynosi 1 ( aktywowana) gdy wartość > 0 (próg) i wyprowadza 0 ( nie aktywowana) w przeciwnym wypadku.
Świetnie. Więc to tworzy funkcję aktywacji dla neuronu. Nie ma żadnych pomyłek. Jednak są pewne wady tego rozwiązania. Aby zrozumieć to lepiej, pomyśl o następującym.
Załóżmy, że tworzysz klasyfikator binarny. Coś, co powinno powiedzieć „tak” lub „nie” ( aktywować lub nie aktywować ). Funkcja Step mogłaby to dla ciebie zrobić! To jest dokładnie to co robi, mówi 1 lub 0. Teraz pomyśl o przypadku użycia, w którym chciałbyś, aby wiele takich neuronów było połączonych, aby wprowadzić więcej klas. Klasa1, klasa2, klasa3 itd. Co się stanie, jeśli więcej niż jeden neuron zostanie „aktywowany”. Wszystkie neurony dadzą na wyjściu 1 (z funkcji krokowej). Co teraz zdecydujesz? Która klasa to jest? Hmm trudne, skomplikowane.
Chciałbyś, aby sieć aktywowała tylko 1 neuron, a inne powinny być 0 ( tylko wtedy mógłbyś powiedzieć, że sklasyfikowała poprawnie/ zidentyfikowała klasę ). Ah! To jest trudniejsze do trenowania i zbieżności w ten sposób. Byłoby lepiej, gdyby aktywacja nie była binarna i zamiast tego mówiłaby „50% aktywowane” lub „20% aktywowane” i tak dalej. I wtedy, jeśli więcej niż 1 neuron aktywuje, można by znaleźć, który neuron ma „najwyższą aktywację” i tak dalej ( lepiej niż max, softmax, ale zostawmy to na razie ).
W tym przypadku również, jeśli więcej niż 1 neuron mówi „100% aktywowany”, problem nadal istnieje.Wiem! Ale..ponieważ istnieją pośrednie wartości aktywacji dla wyjścia, uczenie może być gładsze i łatwiejsze ( mniej wiggly ) i szanse na więcej niż 1 neuron jest 100% aktywowany jest mniejsza w porównaniu do funkcji kroku podczas szkolenia ( również w zależności od tego, co trenujesz i dane ).
Ok, więc chcemy coś, aby dać nam pośrednie ( analogowe ) wartości aktywacji, a nie mówiąc „aktywowane” lub nie ( binarne ).
Pierwszą rzeczą, która przychodzi nam do głowy byłaby funkcja liniowa.
Funkcja liniowa
A = cx
Funkcja liniowa, gdzie aktywacja jest proporcjonalna do wejścia ( które jest sumą ważoną z neuronu ).
W ten sposób daje zakres aktywacji, więc nie jest to aktywacja binarna. Zdecydowanie możemy połączyć kilka neuronów razem i jeśli więcej niż 1 strzela, moglibyśmy wziąć max ( lub softmax) i zdecydować w oparciu o to. Więc to też jest ok. Następnie, jaki jest z tym problem?
Jeśli jesteś zaznajomiony z zejściem gradientowym dla szkolenia, zauważyłbyś, że dla tej funkcji pochodna jest stała.
A = cx, pochodna względem x jest c. Oznacza to, że gradient nie ma związku z X. Jest to stały gradient i zejście będzie na stałym gradiencie. Jeśli jest błąd w przewidywaniu, to zmiany dokonane przez wsteczną propagację są stałe i nie zależą od zmiany danych wejściowych delta(x) !!!
To nie jest takie dobre! ( nie zawsze, ale wytrzymaj ze mną ). Jest też inny problem. Pomyśl o połączonych warstwach. Każda warstwa jest aktywowana przez funkcję liniową. Ta aktywacja z kolei trafia do następnego poziomu jako wejście, a druga warstwa oblicza sumę ważoną na tym wejściu, a ono z kolei wystrzeliwuje w oparciu o inną liniową funkcję aktywacji.
Nieważne ile mamy warstw, jeśli wszystkie są liniowe w naturze, ostateczna funkcja aktywacji ostatniej warstwy jest niczym innym jak tylko liniową funkcją wejścia pierwszej warstwy! Zatrzymaj się na chwilę i pomyśl o tym.
To oznacza, że te dwie warstwy ( lub N warstw ) mogą być zastąpione przez jedną warstwę. Ach! Właśnie straciliśmy możliwość układania warstw w ten sposób. Bez względu na to, jak układamy, cała sieć jest nadal równoważna pojedynczej warstwie z liniową aktywacją ( kombinacja funkcji liniowych w sposób liniowy jest nadal inną funkcją liniową ).
Przejdźmy dalej, dobrze?
Funkcja sigmoidalna
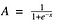
Dobrze, wygląda to gładko i „step function like”. Jakie są z tego korzyści? Zastanów się nad tym przez chwilę. Po pierwsze, jest ona nieliniowa w swojej naturze. Kombinacje tej funkcji są również nieliniowe! Świetnie. Teraz możemy układać warstwy. A co z binarnymi aktywacjami? Tak, to też! To da analogową aktywację w przeciwieństwie do funkcji krokowej. Ma też gładki gradient.
I jeśli zauważysz, między wartościami X -2 do 2, wartości Y są bardzo strome. Co oznacza, że jakiekolwiek małe zmiany w wartościach X w tym regionie spowodują, że wartości Y zmienią się znacząco. Ach, to znaczy, że ta funkcja ma tendencję do doprowadzenia wartości Y do obu końców krzywej.
Wygląda jak to jest dobre dla klasyfikatora biorąc pod uwagę jego właściwości? Tak, rzeczywiście tak jest. Ma tendencję do przynoszenia aktywacji po obu stronach krzywej (powyżej x = 2 i poniżej x = -2 na przykład). Dokonywanie wyraźnych rozróżnień na prediction.
Inną zaletą tej funkcji aktywacji jest, w przeciwieństwie do funkcji liniowej, wyjście funkcji aktywacji jest zawsze będzie w zakresie (0,1) w porównaniu do (-inf, inf) funkcji liniowej. Więc mamy nasze aktywacje związane w zakresie. Dobrze, to nie będzie wysadzać aktywacji wtedy.
To jest świetne. Funkcje sigmoidalne są obecnie jednymi z najczęściej używanych funkcji aktywacji. Jakie są z tym problemy?
Jeśli zauważysz, na obu końcach funkcji sigmoidalnej, wartości Y mają tendencję do reagowania bardzo słabo na zmiany w X. Co to oznacza? Gradient w tym regionie będzie mały. To rodzi problem „znikających gradientów”. Hmm. Więc co się stanie, gdy aktywacje osiągną „prawie poziomą” część krzywej po obu stronach?
Gradient jest mały lub zniknął (nie można dokonać znaczącej zmiany z powodu bardzo małej wartości). Sieć odmawia dalszego uczenia się lub jest drastycznie powolna (w zależności od przypadku użycia i dopóki gradient / obliczenia nie zostaną uderzone przez limity wartości zmiennoprzecinkowych). Istnieją sposoby na obejście tego problemu i sigmoida jest nadal bardzo popularna w problemach klasyfikacji.
Funkcja tanh
Inną funkcją aktywacji, która jest używana jest funkcja tanh.
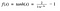
Hm. To wygląda bardzo podobnie do sigmoidy. W rzeczywistości jest to skalowana funkcja sigmoidalna!

Ok, teraz to ma cechy podobne do sigmoidy, którą omawialiśmy powyżej. Jest nieliniowy w naturze, więc świetnie, że możemy układać warstwy! Jest związana z zakresem (-1, 1), więc nie ma obaw o wysadzenie aktywacji. Jednym punktem, o którym należy wspomnieć jest to, że gradient jest silniejszy dla tanh niż sigmoid (pochodne są bardziej strome). Decyzja pomiędzy sigmoid lub tanh będzie zależeć od twoich wymagań co do siły gradientu. Podobnie jak sigmoid, tanh ma również problem znikającego gradientu.
Tanh jest również bardzo popularną i szeroko stosowaną funkcją aktywacji.
ReLu
Później przychodzi funkcja ReLu,
A(x) = max(0,x)
Funkcja ReLu jest jak pokazano powyżej. Daje ona wyjście x, jeśli x jest dodatnie i 0 w przeciwnym wypadku.
Na pierwszy rzut oka wyglądałoby to tak, jakby miało te same problemy z funkcją liniową, ponieważ jest ona liniowa w osi dodatniej. Po pierwsze, ReLu jest nieliniowy w naturze. I kombinacje ReLu są również nieliniowe! ( w rzeczywistości jest to dobry aproksymator. Każda funkcja może być aproksymowana kombinacjami ReLu). Świetnie, więc to oznacza, że możemy układać warstwy. Nie jest to jednak związane. Zakres ReLu to [0, inf). Oznacza to, że może wysadzić aktywację.
Innym punktem, który chciałbym tutaj omówić, jest rozproszenie aktywacji. Wyobraź sobie dużą sieć neuronową z dużą ilością neuronów. Użycie sigmoidy lub tanh spowoduje, że prawie wszystkie neurony będą strzelać w sposób analogowy ( pamiętasz? ). Oznacza to, że prawie wszystkie aktywacje będą przetwarzane w celu opisania wyjścia sieci. Innymi słowy, aktywacja jest gęsta. Jest to kosztowne. Idealnie chcielibyśmy, aby kilka neuronów w sieci nie aktywowało się, a tym samym uczyniło aktywacje rzadkimi i wydajnymi.
ReLu daje nam tę korzyść. Wyobraźmy sobie sieć z losowo zainicjalizowanymi wagami (lub znormalizowanymi) i prawie 50% sieci daje 0 aktywacji z powodu właściwości ReLu (wyjście 0 dla ujemnych wartości x). Oznacza to, że mniej neuronów się odpala ( sparse activation ) i sieć jest lżejsza. Woah, fajnie! ReLu wydaje się być niesamowity! Tak jest, ale nic nie jest bezbłędne… Nawet ReLu.
Z powodu poziomej linii w ReLu (dla ujemnego X), gradient może iść w kierunku 0. Dla aktywacji w tym regionie ReLu, gradient będzie równy 0, z powodu czego wagi nie będą dostosowywane podczas zejścia. Oznacza to, że neurony, które znajdą się w tym stanie, przestaną reagować na zmiany błędu/wejścia (po prostu dlatego, że gradient jest równy 0, nic się nie zmienia). Jest to tak zwany problem umierającego ReLu. Ten problem może spowodować, że kilka neuronów po prostu umrze i nie będzie reagować, czyniąc znaczną część sieci pasywną. Istnieją odmiany ReLu, które łagodzą ten problem poprzez proste przekształcenie linii poziomej w składową nie poziomą. Na przykład y = 0.01x dla x<0 sprawi, że będzie to linia lekko nachylona, a nie pozioma. To jest właśnie nieszczelne ReLu. Istnieją również inne warianty. Główną ideą jest pozwolić gradientowi być niezerowym i odzyskać podczas szkolenia ostatecznie.
ReLu jest mniej kosztowny obliczeniowo niż tanh i sigmoid, ponieważ obejmuje prostsze operacje matematyczne. Jest to dobry punkt do rozważenia, gdy projektujemy głębokie sieci neuronowe.
Ok, teraz, który z nich używamy?
Teraz, które funkcje aktywacji użyć. Czy to znaczy, że po prostu używamy ReLu do wszystkiego, co robimy? Albo sigmoid lub tanh? Cóż, tak i nie. Kiedy wiesz, że funkcja, którą próbujesz aproksymować ma pewne cechy, możesz wybrać funkcję aktywacji, która będzie aproksymować funkcję szybciej, co prowadzi do szybszego procesu szkolenia. Na przykład, sigmoida działa dobrze dla klasyfikatora (zobacz wykres sigmoidy, czyż nie pokazuje on właściwości idealnego klasyfikatora? ) ponieważ aproksymacja funkcji klasyfikatora jako kombinacji sigmoidy jest łatwiejsza niż na przykład ReLu. Co doprowadzi do szybszego procesu szkolenia i konwergencji. Możesz również użyć własnych niestandardowych funkcji! Jeśli nie znasz natury funkcji, której próbujesz się nauczyć, to może sugerowałbym zacząć od ReLu, a następnie pracować wstecz. ReLu działa przez większość czasu jako ogólny aproksymator!
W tym artykule próbowałem opisać kilka funkcji aktywacji używanych powszechnie. Istnieją również inne funkcje aktywacji, ale ogólna idea pozostaje taka sama. Badania nad lepszymi funkcjami aktywacji wciąż trwają. Mam nadzieję, że zrozumieliście ideę funkcji aktywacji, dlaczego są one używane i jak decydujemy, której z nich użyć.
.