Teoria grafów – typy grafów

Istnieją różne typy grafów w zależności od liczby wierzchołków, liczby krawędzi, wzajemnych połączeń i ich ogólnej struktury. W tym rozdziale omówimy tylko kilka ważnych typów grafów.

Wykres zerowy

Wykres nieposiadający krawędzi nazywamy wykresem zerowym.

Przykład

W powyższym wykresie są trzy wierzchołki o nazwach 'a’, 'b’ i 'c’, ale nie ma między nimi żadnych krawędzi. Stąd jest to graf zerowy.

Graf trywialny

Graf z tylko jednym wierzchołkiem nazywamy grafem trywialnym.

Przykład

W przedstawionym powyżej grafie jest tylko jeden wierzchołek 'a’ bez żadnych innych krawędzi. Stąd jest to graf trywialny.

Graf nieskierowany

Graf nieskierowany zawiera krawędzie, ale nie są to krawędzie skierowane.

Przykład

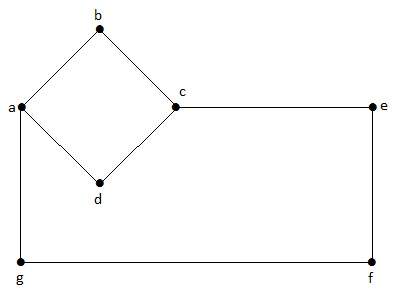
W tym grafie 'a’, 'b’, 'c’, 'd’, 'e’, 'f’, 'g’ są wierzchołkami, a 'ab’, 'bc’, 'cd’, 'da’, 'ag’, 'gf’, 'ef’ są krawędziami grafu. Ponieważ jest to graf nieskierowany, krawędzie „ab” i „ba” są takie same. Podobnie inne krawędzie również są traktowane w ten sam sposób.

Graf skierowany

W grafie skierowanym każda krawędź ma kierunek.

Przykład

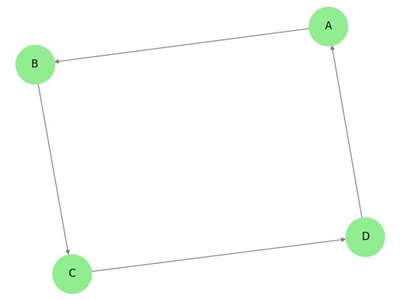
W powyższym grafie mamy siedem wierzchołków „a”, „b”, „c”, „d”, „e”, „f” i „g” oraz osiem krawędzi „ab”, „cb”, „dc”, „ad”, „ec”, „fe”, „gf” i „ga”. Ponieważ jest to graf skierowany, każda krawędź jest oznaczona strzałką wskazującą jej kierunek. Zauważmy, że w grafie skierowanym krawędź 'ab’ jest różna od krawędzi 'ba’.

Graf prosty

Graf bez pętli i bez krawędzi równoległych nazywamy grafem prostym.

• Maksymalna liczba krawędzi możliwa do uzyskania w pojedynczym grafie o 'n’ wierzchołkach wynosi nC2, gdzie nC2 = n(n – 1)/2.

• Liczba możliwych grafów prostych o 'n’ wierzchołkach = 2nc2 = 2n(n-1)/2.

Przykład

W poniższym grafie są 3 wierzchołki z 3 krawędziami, co jest maksymalną liczbą wykluczającą krawędzie równoległe i pętle. Można to udowodnić korzystając z powyższych wzorów.

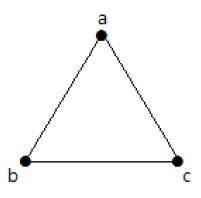
Maksymalna liczba krawędzi przy n=3 wierzchołkach –

nC2 = n(n–1)/2 = 3(3–1)/2 = 6/2 = 3 edges

Maksymalna liczba prostych w grafie przy n=3 wierzchołkach –

2nC2 = 2n(n-1)/2 = 23(3-1)/2 = 23 = 8

Tych 8 grafów jest jak na rysunku poniżej –

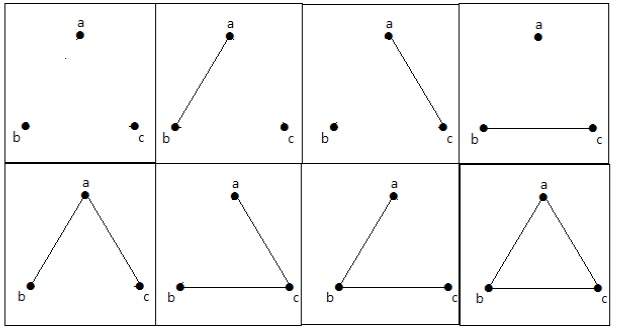
Graf połączony

O grafie G mówi się, że jest połączony, jeśli między każdą parą wierzchołków istnieje ścieżka. Dla każdego wierzchołka w grafie powinna istnieć co najmniej jedna krawędź. Tak, że możemy powiedzieć, że jest podłączony do jakiegoś innego wierzchołka po drugiej stronie krawędzi.

Przykład

W poniższym grafie każdy wierzchołek ma własną krawędź połączoną z inną krawędzią. Jest to więc graf połączony.

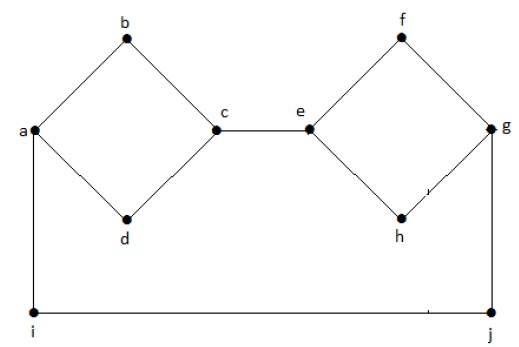
Graf rozłączny

Graf G jest rozłączny, jeśli nie zawiera co najmniej dwóch połączonych wierzchołków.

Przykład 1

Poniższy graf jest przykładem grafu rozłącznego, w którym istnieją dwa składniki, jeden z wierzchołkami „a”, „b”, „c”, „d” i drugi z wierzchołkami „e”, „f”, „g”, „h”.

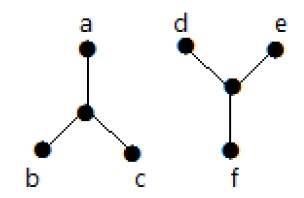
Dwa składniki są niezależne i nie są ze sobą połączone. Stąd nazywamy go grafem rozłącznym.

Przykład 2

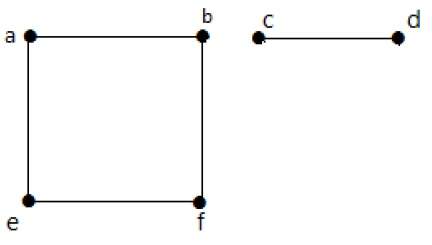
W tym przykładzie istnieją dwie niezależne składowe, a-b-f-e i c-d, które nie są ze sobą połączone. Stąd jest to graf rozłączny.

Graf regularny

O grafie G mówi się, że jest regularny, jeśli wszystkie jego wierzchołki mają ten sam stopień. W grafie, jeśli stopień każdego wierzchołka wynosi „k”, to graf nazywamy „k-grafem regularnym”.

Przykład

W poniższych grafach wszystkie wierzchołki mają ten sam stopień. Zatem grafy te nazywamy grafami regularnymi.

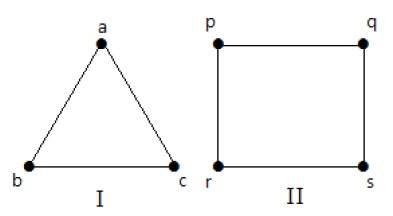
W obu grafach wszystkie wierzchołki mają stopień 2. Są one nazywane grafami 2-Regular.

Grafy pełne

Grafy proste o „n” wzajemnych wierzchołkach nazywamy grafami pełnymi i oznaczamy je symbolem „Kn”. W grafie wierzchołek powinien mieć krawędzie ze wszystkimi innymi wierzchołkami, wtedy nazywamy go grafem zupełnym.

Innymi słowy, jeśli wierzchołek jest połączony ze wszystkimi innymi wierzchołkami w grafie, wtedy nazywamy go grafem zupełnym.

Przykład

W następujących grafach każdy wierzchołek w grafie jest połączony ze wszystkimi pozostałymi wierzchołkami w grafie z wyjątkiem siebie samego.

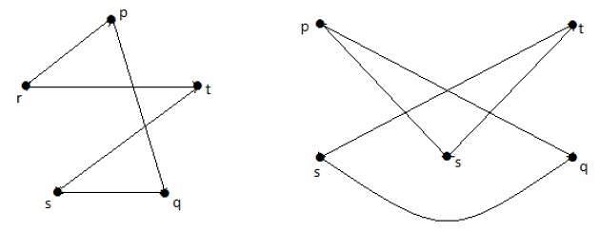
W grafie I,

.

	a	b	c
a	Niepołączony	Połączony	Połączony
b	Connected	Not Connected	Connected
c	Connected	Connected	Not Connected

W grafie II,

.

	p	q	r	s
p	Not Connected	Connected	Connected	Connected	Connected	Połączone
q	Połączone	Niepołączone	Połączone	Połączone
r	Połączone	Connected	Not Connected	Connected
s	Connected	Connected	Connected	Not Connected

Cycle Graph

A simple graph with 'n’ vertices (n >= 3) and 'n’ edges is called a cycle graph if all its edges form a cycle of length 'n’.

Jeśli stopień każdego wierzchołka w grafie wynosi dwa, to nazywamy go grafem cyklicznym.

Notacja – Cn

Przykład

Przyjrzyjrzyj się następującym grafom –

• Graf I ma 3 wierzchołki i 3 krawędzie, które tworzą cykl „ab-bc-ca”.

• Grafik II ma 4 wierzchołki i 4 krawędzie tworzące cykl 'pq-qs-sr-rp’.

• Grafik III ma 5 wierzchołków i 5 krawędzi tworzących cykl 'ik-km-ml-lj-ji’.

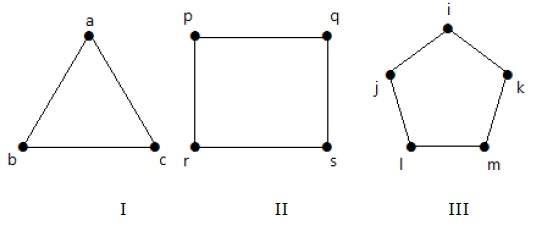
Więc wszystkie podane grafy są grafami cyklicznymi.

Wykres kołowy

Wykres kołowy otrzymuje się z grafu cyklicznego Cn-1 przez dodanie nowego wierzchołka. Ten nowy wierzchołek nazywamy Piastem, który jest połączony ze wszystkimi wierzchołkami grafu Cn.

Notacja – Wn

No. of edges in Wn = No. of edges from hub to all other vertices + No. of edges from all other nodes in cycle graph without a hub. = (n–1) + (n–1) = 2(n–1)

Przykład

Przyjrzyjrzyj się poniższym grafom. Wszystkie są grafami koła.

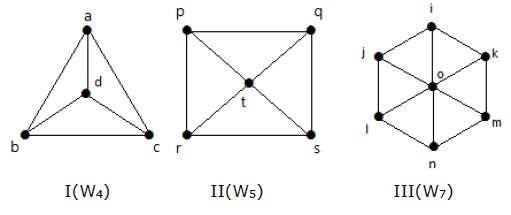
W grafie I, otrzymujemy go z C3 przez dodanie wierzchołka w środku o nazwie 'd’. Oznaczamy go jako W4.

Number of edges in W4 = 2(n-1) = 2(3) = 6

W grafie II, otrzymujemy go z C4 przez dodanie wierzchołka w środku o nazwie 't’. Jest on oznaczony jako W5.

Number of edges in W5 = 2(n-1) = 2(4) = 8

W grafie III, jest on otrzymany z C6 przez dodanie wierzchołka w środku o nazwie „o”. Oznaczamy go jako W7.

Number of edges in W4 = 2(n-1) = 2(6) = 12

Wykres cykliczny

Wykres posiadający co najmniej jeden cykl nazywamy wykresem cyklicznym.

Przykład

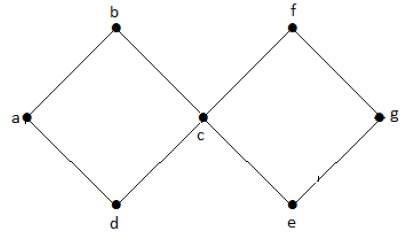
W powyższym przykładowym wykresie mamy dwa cykle a-b-c-d-a oraz c-f-g-e-c. Stąd nazywamy go grafem cyklicznym.

Wykres acykliczny

Wykres bez cykli nazywamy grafem acyklicznym.

Przykład

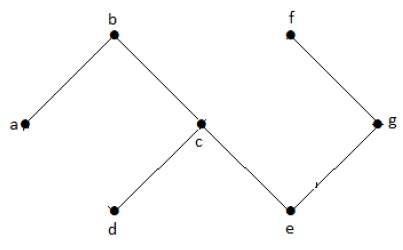
W powyższym przykładowym grafie nie mamy żadnych cykli. Stąd jest to graf niecykliczny.

Graf dwudzielny

Graf prosty G = (V, E) z partycją wierzchołków V = {V1, V2} nazywamy grafem dwudzielnym, jeśli każda krawędź E łączy wierzchołek w V1 z wierzchołkiem w V2.

W ogólności graf dwudzielny ma dwa zbiory wierzchołków, powiedzmy V1 i V2, a jeśli narysowana jest krawędź, to powinna ona łączyć dowolny wierzchołek ze zbioru V1 z dowolnym wierzchołkiem ze zbioru V2.

Przykład

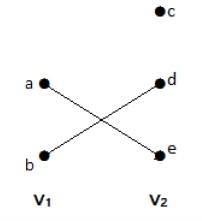
W tym grafie można zaobserwować dwa zbiory wierzchołków – V1 i V2. Tutaj dwie krawędzie o nazwach 'ae’ i 'bd’ łączą wierzchołki dwóch zbiorów V1 i V2.

Kompletny graf dwudzielny

O grafie dwudzielnym 'G’, G = (V, E) z partycją V = {V1, V2} mówi się, że jest kompletnym grafem dwudzielnym, jeśli każdy wierzchołek w V1 jest połączony z każdym wierzchołkiem V2.

W ogólności, pełny graf dwudzielny łączy każdy wierzchołek ze zbioru V1 z każdym wierzchołkiem ze zbioru V2.

Przykład

Następujący graf jest pełnym grafem dwudzielnym, ponieważ posiada krawędzie łączące każdy wierzchołek ze zbioru V1 z każdym wierzchołkiem ze zbioru V2.

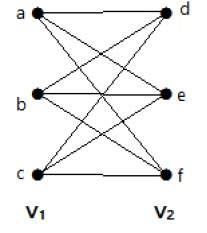
Jeżeli |V1| = m i |V2| = n, to pełny graf dwudzielny oznaczamy przez Km, n.

• Km,n ma (m+n) wierzchołków i (mn) krawędzi.

• Km,n jest grafem regularnym, jeśli m=n.

W ogólności graf dwudzielny zupełny nie jest grafem pełnym.

Km,n jest grafem zupełnym, jeśli m=n=1.

Maksymalna liczba krawędzi w grafie dwudzielnym o n wierzchołkach wynosi

Jeśli n=10, k5, 5= ⌊n2/4⌋ = ⌊102/4⌋ = 25

Podobnie K6, 4=24

K7, 3=21

K8, 2=16

K9, 1=9

Jeśli n=9, k5, 4 = ⌊n2/4⌋ = ⌊92/4⌋ = 20

Podobnie K6, 3=18

K7, 2=14

K8, 1=8

’G’ jest grafem dwudzielnym, jeśli 'G’ nie ma cykli nieparzystej długości. Szczególnym przypadkiem grafu dwudzielnego jest graf gwiaździsty.

Graf gwiaździsty

Zupełny graf dwudzielny postaci K1, n-1 jest grafem gwiaździstym o n wierzchołkach. Graf gwiaździsty jest grafem dwudzielnym zupełnym, jeśli pojedynczy wierzchołek należy do jednego zbioru, a wszystkie pozostałe wierzchołki należą do drugiego zbioru.

Przykład

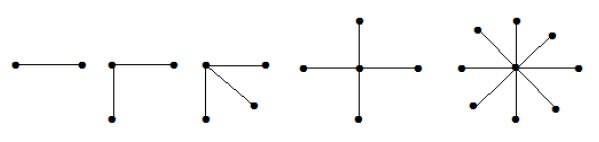
W powyższych grafach spośród „n” wierzchołków wszystkie „n-1” wierzchołki są połączone z jednym wierzchołkiem. Stąd jest on w postaci K1, n-1, które są grafami gwiaździstymi.

Dopełnienie grafu

Niech 'G-’ będzie grafem prostym z pewnymi wierzchołkami takimi jak w 'G’ i krawędź {U, V} jest obecna w 'G-’, jeśli ta krawędź nie jest obecna w G. Oznacza to, że dwa wierzchołki są sąsiadujące w 'G-’, jeśli te dwa wierzchołki nie są sąsiadujące w G.

Jeśli krawędzie, które istnieją w grafie I, nie występują w innym grafie II i jeśli zarówno graf I, jak i graf II są połączone razem, tworząc graf pełny, to graf I i graf II nazywamy wzajemnie dopełnieniami.

Przykład

W poniższym przykładzie graf-I ma dwie krawędzie „cd” i „bd”. Jego dopełnienie graf-II ma cztery krawędzie.

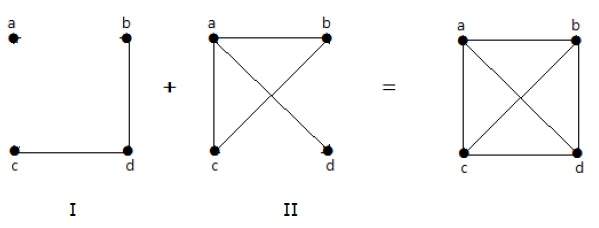
Zauważmy, że krawędzie w grafie-I nie występują w grafie-II i odwrotnie. Stąd połączenie obu grafów daje graf pełny o 'n’ wierzchołkach.

Uwaga – połączenie dwóch grafów komplementarnych daje graf pełny.

Jeżeli 'G’ jest dowolnym grafem prostym, to

|E(G)| + |E(’G-’)| = |E(Kn)|, gdzie n = liczba wierzchołków w grafie.

Przykład

Pozostawmy 'G’ jako graf prosty o dziewięciu wierzchołkach i dwunastu krawędziach, znajdźmy liczbę krawędzi w 'G-’.

Mamy, |E(G)| + |E(’G-’)| = |E(Kn)|

12 + |E(’G-’)| =

12 + |E(’G-’)| =

.