Wprowadzenie
Niniejsza strona zawiera przegląd równania ciągłości, które wymusza zachowanie masy w analizie eulerowskiej. Nie jest to ściśle opis zachowania materiału, ale wynikowe równanie jest często używane jako tożsamość do toalgebraicznego manipulowania modelami konstytutywnymi opisującymi zachowanie materiału. Warto więc zapoznać się z tym zagadnieniem. Jest ono również kluczowe dla analizy przepływu płynów, ponieważ klasyczne analizy płynów nie mogą być Lagrangianem, ponieważ pozycje wszystkich cząstek płynu w chwili (t = 0) są nieznane.
Zachowanie masy
Równanie ciągłości odzwierciedla fakt, że masa jest zachowana w każdej niejądrowej analizie mechaniki continuum. Równanie jest rozwijane przez zsumowanie szybkości, z jaką masa wpływa i wypływa z objętości kontrolnej, i ustawienie przepływu netto równego szybkości zmiany masy w tej objętości. Jest to pokazane na poniższym rysunku.
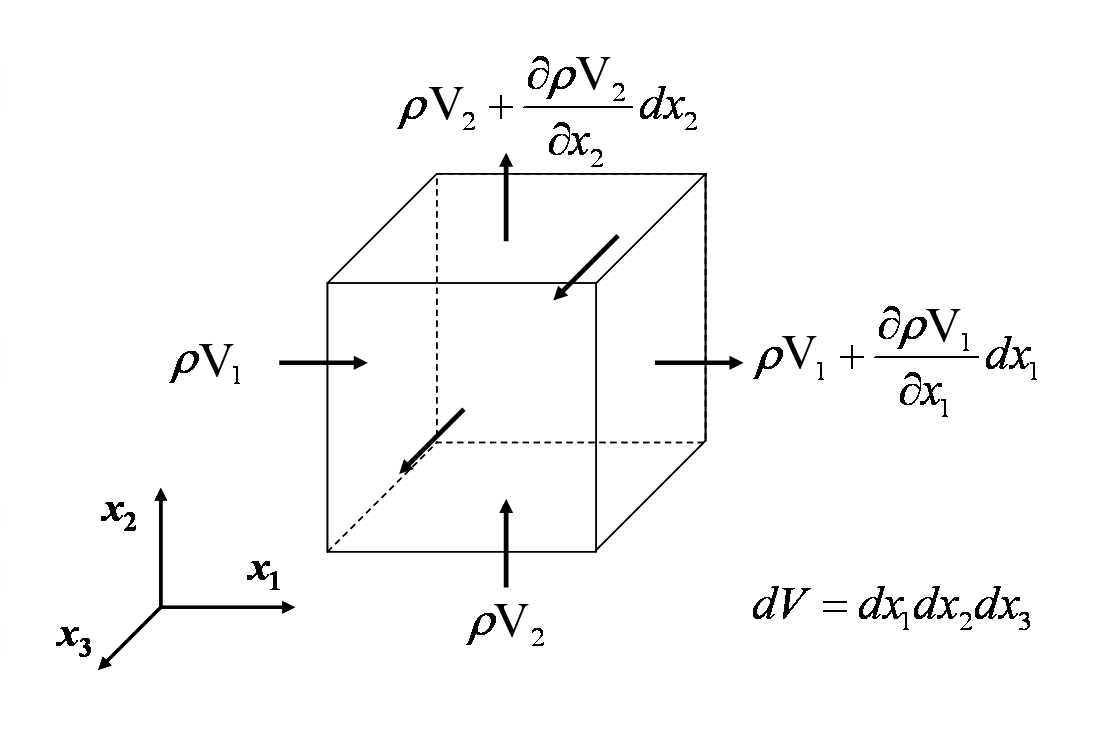
Equating all the mass flow rates into and out of the differential controlvolume gives
Cancelling terms and dividing through by \(dx_1 dx_2 dx_3\) daje
, a ponowne uporządkowanie daje
Można to zapisać zwięźle jako

Ważne punkty
To są ostateczne, są to ostateczne, kompletne i najbardziej ogólne formy równania ciągłości, które wymusza zachowanie masy. Ma ono zastosowanie do wszystkich materiałów, nie tylko płynów. Ma więc zastosowanie również do ciał stałych. Zauważmy, że jest to pojedyncze równanie skalarne i ma charakter eulerowski, ponieważ równania gradientowe są równaniami \({część \ nad \częścią x_i}), a nie \({część \ nad \częścią X_i}).
Można by się zastanawiać, czy istnieje Lagrangianowy odpowiednik eulerowskiej formy tego równania. Istnieje. Zwykle zapisuje się go jako
Po prostu stwierdza, że różniczkowy zrąb masy w stanie odkształconym musi być równy jego pierwotnej wartości w stanie niezniekształconym. Istnieje kilka szczególnych przypadków równania ciągłości.Pierwszy z nich występuje, gdy przepływ jest w stanie ustalonym. W tym przypadku pochodna względem czasu wynosi zero, pozostawiając.
Drugim szczególnym przypadkiem jest przypadek nieściśliwości, tzn, \W tym przypadku pochodna względem czasu jest równa zeru i można ją wypisać z równania, pozostawiając jedynie
Ten wynik jest na tyle prosty, że często jest rozszerzany. Pierwszym krokiem jest zastosowanie reguły iloczynu do członu dywergencyjnego w równaniu ciągłości.
A następnie zauważamy, że pochodna gęstości({D ¨partial ¨rho ¨over ¨partial t} + {{bf v} ¨cdot ¨nabla ¨rho¨) jest po prostu pochodną materialną gęstości,¨({D ¨rho ¨over D t}¨).
Więc równanie ciągłości można również zapisać jako
∗ Jeżeli materiał jest nieściśliwy, to ∗ nie może się zmieniać, więc ∗ ( {D ™rho ™over D t} ™) musi być równe zeru, a następnie dzielimy przez \(\) (ponieważ nie jest równe zero), aby otrzymać

Równanie ciągłości Przykład
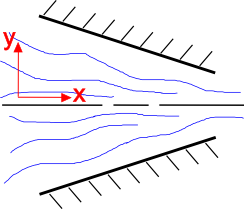
Intuicyjne jest, że przepływ płynu przyspiesza wraz ze zmniejszaniem się jego przekroju poprzecznego, jak pokazano po prawej stronie. Wyjaśnia to równanie ciągłości. Rozważmy dwuwymiarowe pole przepływu nieściśliwego płynu w stanie ustalonym. Równanie ciągłości dla tej sytuacji ma postać
Zacznijmy od spojrzenia na składową y przepływu, ∗(v_2}). Geometria zbiegającej się dyszy zmusza składową y do przepływu w górę, gdy y jest mniejsza od 0, i w dół, gdy y jest mniejsza od 0. Tak więc \u2002 \u2008 \u2008 \u2008 \u2008 \u2008 \u2008 \u2008 \u2008 \u2008 \u2008 \u2008 \u2008 \u2008
Ale równanie ciągłości nakazuje, aby suma dwóch pochodnych cząstkowych była równa zeru. Więc jeśli druga jest mniejsza od zera, to
A to oznacza, że przepływ płynu musi być przyspieszony.