Równania Lotki-Volterry opisują ekologiczny model drapieżnik-prezerwuar (lub pasożyt-żywiciel), który zakłada, że, dla zestawu stałych dodatnich 
(tempo wzrostu ofiary), 
(tempo, w jakim drapieżniki niszczą ofiarę), 
(tempo śmierci drapieżników) i 
(tempo, w jakim drapieżniki rosną poprzez konsumpcję ofiary), spełnione są następujące warunki.
1. Populacja ofiar 
rośnie w tempie 
(proporcjonalnym do liczby ofiar), ale jednocześnie jest niszczona przez drapieżniki w tempie 
(proporcjonalnym do iloczynu liczby ofiar i drapieżników).
2. Populacja drapieżników 
maleje w tempie 
(proporcjonalnym do liczby drapieżników), ale rośnie w tempie 
(znów proporcjonalnym do iloczynu liczb ofiar i drapieżników).
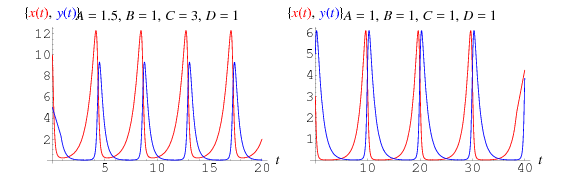
Daje to równania różniczkowe sprzężone
 |
 |
 |
(1)
|
 |
 |
 |
(2)
|
, których rozwiązania są wykreślone powyżej, gdzie ofiary są zaznaczone na czerwono, a drapieżniki na niebiesko. W tego rodzaju modelu krzywa ofiary zawsze prowadzi do krzywej drapieżnika.
Punkty krytyczne występują, gdy 
, więc
 |
 |
 |
(3)
|
 |
 |
 |
(4)
|
Jedyny punkt stacjonarny znajduje się zatem w punkcie 
.