Tak jak ciasto możesz mieć 2 małe kawałki lub 1 kawałek dwa razy większy i jest to ta sama ilość. Stąd wiele ułamków jest równoważnych, jak 2/5 i 4/10.


Any Number Can Be Written As a Fraction
Write any whole number over 1 to make it a fraction since the total number of parts in any undivided whole is one.
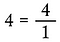
Mnożenie ułamków prosto w poprzek
Mnożenie ułamków jest łatwe, wystarczy mnożyć prosto w poprzek.
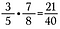
Uwaga: Liczby mieszane muszą być najpierw zamienione na ułamki niewłaściwe, czytaj dalej, aby dowiedzieć się więcej na ten temat.
Multiply By Any Form of One Anytime
Liczba 1 jest nazywana tożsamością multiplikatywną, ponieważ możemy ją pomnożyć przez dowolną liczbę i liczba pozostaje taka sama. Jest to ważne dla ułamków, ponieważ często musimy zmienić wygląd ułamka bez faktycznej zmiany jego wartości.
Na przykład, mogę zmienić 1/3 w równoważny ułamek 3/9 przez pomnożenie przez 3/3.
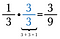
Dodawanie i odejmowanie równych wielkościowo części
Przy dodawaniu i odejmowaniu ułamków mianowniki muszą być takie same. To ma sens. Jeśli chcemy łączyć lub zabierać części, musimy mówić o częściach tej samej wielkości, w przeciwnym razie będzie to mylące.
Co więc zrobić, jeśli twoje ułamki nie mają tych samych wielkości?
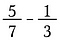
Mnożymy przez jeden, aby zmienić mianowniki na wspólną wielkość. Zasadniczo, dzielimy ułamki na mniejsze części, aż będą tej samej wielkości. To się nazywa znalezienie wspólnego mianownika.
Prawdę mówiąc, każdy wspólny mianownik będzie zrobić, ale ludzie wolą znaleźć najmniejszy z nich. W tym przypadku najmniejszą liczbą, w którą zarówno 7 jak i 3 wchodzą bez reszty jest 21. Więc pomnóż pierwszy ułamek przez 3/3, a drugi przez 7/7.
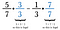
Jeśli nie możesz wymyślić najmniejszego wspólnego mianownika, zawsze możesz pomnożyć każdy ułamek przez przeciwny mianownik. Czasami, tak jak w tym przypadku, okazuje się, że jest to najmniejszy wspólny mianownik. Jeśli tak nie jest, po prostu zmniejsz odpowiedź na końcu.
Gdy mianowniki się zgadzają, odejmij liczniki, aby otrzymać 8/21.
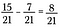
To działa tak, jak można by się spodziewać. Obrazowo, zacznij od 15 klocków z 21 ogółem.

Usuń kolorowanie z 7 z 15 niebieskich klocków.

Co pozostawia 8/21 zgodnie z oczekiwaniami.
Wymień najpierw liczby mieszane
Liczba mieszana to połączenie liczby całkowitej i ułamka.
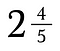
Liczby mieszane nie grają dobrze z innymi ułamkami. Dobrym pomysłem jest przekształcenie ich najpierw w ułamki niewłaściwe.
Uwaga: Ułamek niewłaściwy to ułamek, którego licznik jest większy niż mianownik, dlatego ma wartość większą niż jeden.
Konwersja liczby mieszanej to naprawdę dodawanie
Aby przekształcić 2 i 4/5 w ułamek niewłaściwy dodaj 2 + 4/5.
Krok 1: Zacznij od przepisania 2 jako 2/1.
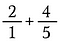
Krok 2: Pomnóż 2/1 przez 5/5, aby otrzymać ułamek równoważny 10/5, który ma pożądany wspólny mianownik 5.
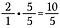
Krok 3: Dodaj 10/5 + 4/5.
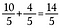
Naszym wynikiem jest ułamek niewłaściwy równoważny 14/5.
Aby przekonwertować z powrotem na liczbę mieszaną wykonaj dzielenie. Na przykład, 5 wchodzi do 14 dwa razy (ponieważ 5 x 2 = 10) z 4 kawałkami pozostałymi.
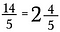
Compare Fractions Using The Cross Product
Załóżmy, że chcieliśmy określić, który jest większy: 5/12 czy 6/13.
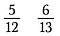
Krok pierwszy: Pomnóż jedną przekątną i zapisz iloczyn nad licznikiem.
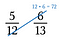
Krok drugi: Pomnożyć drugą przekątną i zapisać jej iloczyn nad licznikiem.
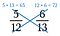
Krok trzeci: Porównaj produkty. Strona z większym iloczynem jest większym ułamkiem. Tak więc w tym przypadku, 5/12 jest mniejsze niż 6/13.
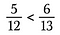
Możemy również określić, czy ułamki są równe używając iloczynów krzyżowych.
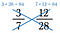
Iloczyn krzyżowy 3/7 i 12/28 wynosi 84, zatem 3/7 = 12/28.
Cancel Anything That Divides to One
Najlepszą rzeczą w ułamkach jest to, że można znaleźć wiele okazji do ich anulowania. Co czyni je szybkimi i łatwymi do zarządzania.
Załóżmy, że mam ułamek 8/10. Zarówno 8 jak i 10 mogą być przepisane z 2 jako czynnikiem.
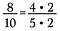
Ponieważ 2/2 = 1, mogę anulować 2’s pozostawiając 4/5 jako zredukowany ułamek.
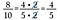
Użyj tej strategii, aby ułatwić sobie również mnożenie ułamków.
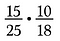
Zacznij od przepisania każdej liczby na czynniki.
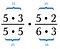
Usuń wszystkie pary liczb, które dzielą się przez 1. Na przykład, 5/5 = 1.
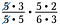
Mam jeszcze jedną parę liczb 5 oraz parę liczb 3, które również dzielą się przez 1.
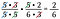
Ups! Mogłem przepisać 6 jako 2 x 3 i anulować parę dwójek. Nie szkodzi, jeśli pominiesz jakiś czynnik, po prostu kontynuuj, aż uzyskasz je wszystkie.
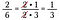
Gdybym pomnożył 15/25 razy 10/18 bezpośrednio byłoby to dużo arytmetyki, używając anulowania wstępnie redukuję ułamki i upraszczam mnożenie.
Użyj mnożenia do dzielenia ułamków
Koncepcja dzielenia ułamków jest łatwa dzięki prostym przykładom, takim jak:

W całości są dwie połówki, więc w 5 całościach jest 10 połówek.
Ale koncepcja ta staje się trudna przy bardziej skomplikowanych ułamkach.
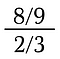
Aby rozwiązać ten problem, wykorzystamy dwa fakty:
- Możemy mnożyć przez dowolną formę jedynki (tj.
- Mnożąc przez odwrotność 3/2, czyli przez 2/3, otrzymujemy 1 poprzez anulowanie
Krok pierwszy: Zacznij od mnożenia przez odwrotność nad sobą.
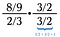
Teraz mamy do rozwiązania dwa mniejsze problemy (niebieski i zielony).
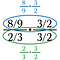
Krok drugi: Anuluj wszystko, co dzieli się na 1 w dolnej (zielonej) frakcji. Powinno to zawsze dawać wynik 1.

Teraz pozostaje nam górny problem do rozwiązania.
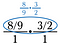
Krok trzeci: Użyj anulowania, aby wstępnie zredukować ułamek. Po wykonaniu tych redukcji pomnóż ułamek w poprzek, aby otrzymać 4/3.

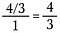
Skrót
To jest mechanika długiej ręki „przerzuć i pomnóż.”
Możemy pominąć mnożenie przez odwrotność na dole, ponieważ zawsze anuluje się do 1. Dlatego wszystko, co musisz zrobić, to pomnożyć licznik przez odwrotność mianownika.

Bonus: Teoria, w przypadku, gdy jesteś zainteresowany…
Wspaniałe pytanie! Aby uogólnić, utwórz dwa ułamki, używając liter a, b, c i d do reprezentowania czterech różnych liczb.
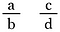
Mnóż oba ułamki przez b-d (umożliwi nam to anulowanie mianowników).
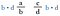
Teraz anuluj b po lewej i d po prawej stronie, ponieważ dzielą się one przez 1. Nie mamy już ułamków, a jedynie iloczyny d-a i c-b.
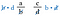
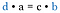
Spójrz z powrotem na oryginalne ułamki. Są to takie same produkty, jak gdybyśmy pomnożyli przekątne. Dlatego skrótem jest porównanie iloczynu krzyżowego.
❤ STAY CONNECTED ❤
Stay up-to-date with everything Math Hacks is up to!