Jak pomóc uczniom, którzy zmagają się z zadaniami słownymi

„Oni znają matematykę. Nie potrafią tylko rozwiązywać zadań słownych. Chodzi o ich umiejętność czytania ze zrozumieniem.”

Pani Hartwell wyjaśniała, dlaczego jej uczniowie mieli problemy z testami stanowymi. Znała swoich uczniów i dokonała obszernej oceny. Była pewna, że ich trudności wynikały z problemów z czytaniem i pisaniem.

„Nie rozumiem, dlaczego czytanie jest tak trudne. Dzieci już zdają testy z plastyki językowej.”

Zostałam połączona z panią Hartwell (i innymi uczniami z jej szkoły) w ramach nowojorskiego programu mającego na celu zwiększenie osiągnięć z matematyki. Celem było wprowadzenie matematyki koncepcyjnej do szkół „poziomu 1”. Były to szkoły, które przodowały w mieście w trzech obszarach. Najniższy dochód, najniższe wyniki testów i najwyższy odsetek uczniów kolorowych.

Słyszałam wyjaśnienie „alfabetyzacji” od innych nauczycieli w programie. I rzeczywiście miało to sens. Jeśli uczniowie znali matematykę, to dlaczego mieli problemy na teście, który zawierał wiele zadań słownych?

Ale był pewien haczyk. W ciągu ostatnich trzech lat, poziom umiejętności czytania i pisania wzrósł z 30% do 40% w całym mieście. W tym samym okresie, wyniki z matematyki pozostały bez zmian.

Gdyby to był problem z czytaniem, wzrost wyników w czytaniu powinien odblokować gwałtowny wzrost w matematyce. Poza tym, język w zadaniach słownych nie wydawał się na tyle skomplikowany, by sprawiać kłopoty.

Następnego dnia miałem odwiedzić klasę pani Hartwell. Zaplanowała ona lekcję poświęconą problemom słownym, więc mogłam zobaczyć ten problem z pierwszej ręki.

Over-Scaffolding Word Problems

Uczniowie siedzieli przy okrągłych stołach, a ona stała z przodu. Ona i jej uczniowie mieli podręczne tablice.

Otworzyli swoje podręczniki na stronie 47, a ona przeczytała na głos zadanie. „Sara ma 40 funtów marchewki dla swoich koni. Jeśli ma 100 koni, to ile funtów dostanie każdy koń?”.

„OK klasa, ona ma 40 funtów, które da każdemu koniowi. Więc jaka operacja jest nam potrzebna?”

Wskazała na tabelę kotwiczną z listą 'słów kluczowych’ dla każdej operacji. Każda z nich była na szczycie listy podziału.

„Podział!” – odpowiedziała klasa.

„Racja. Jak więc podzielić małą liczbę przez dużą?”

Klasa była cicho. Pani Hartwell narysowała vinculum (dom długiego dzielenia) na swojej tablicy. Uczniowie kopiowali jak ona umieściła 40 pod domem i 100 na zewnątrz.

„Teraz 100 nie mieści się w 40, więc musimy dodać dziesiętną.” Zmieniła 40 na 40.0. „Ile razy 100 wchodzi w 400?”

Kilku uczniów zawołało „Cztery!”.

„Dokładnie. Teraz w naszym ilorazie również musimy umieścić część dziesiętną. Nasza ostateczna odpowiedź to?”

Klasa odczytała odpowiedź, „0,4”, z tablicy.

Przydzieliła podobny problem i wskazała na plakat „CUBES” na ścianie. „Pamiętajcie, aby zakreślić liczby i zaznaczyć słowa kluczowe.”

Krążyła, gdy uczniowie pracowali. Niektórzy pytali, gdzie należy umieścić przecinek. Inni mieli problem z wyłożeniem części odejmującej długiego dzielenia. Niektórzy uczniowie pracowali w parach, z których jeden dokonywał obliczeń, podczas gdy drugi kopiował. „Widzicie?” Pani Hartwell zauważyła, że „wszyscy znają matematykę.”

Co poszło nie tak?

Jakkolwiek jest to skrajny przykład, wiele z błędów popełnionych przez panią Hartwell jest w rzeczywistości dość powszechnych.

Nadmierne przysłanianie występuje wtedy, gdy zapewniamy uczniom zbyt wiele wsparcia. Podczas gdy pedagodzy są dumni z tego, że zapewniają uczniom „tyle wsparcia, ile potrzebują”, nadmierne rusztowanie jest czymś innym.

Termin „rusztowanie” pochodzi z pracy Lwa Wygotskiego. To on ukuł termin „Strefa najbliższego rozwoju” (Zone of Proximal Development). ZPD obejmuje rzeczy, które są poza zasięgiem osoby uczącej się. Nie jest w stanie zrobić tego samodzielnie, ale może to zrobić z pomocą. Poprzez „rusztowanie” możemy przenieść te umiejętności do podstawowego zestawu umiejętności ucznia.

Często pomija się fakt, że rusztowanie dotyczy tylko umiejętności już znajdujących się w ZPD ucznia. Istnieje cały szereg umiejętności, które są obecnie poza zasięgiem ucznia. Kiedy próbujemy je rozwijać, wyrządzamy więcej szkody niż pożytku.

Jednym z problemów związanych z nadmiernym rusztowaniem jest to, że uczniowie nigdy nie przyswajają sobie tych umiejętności. Kiedy pomagamy uczniowi w czymś, co jest poza jego ZPD, zawsze będzie on potrzebował naszej pomocy. Przynajmniej do czasu, aż zidentyfikujemy umiejętności pośrednie, które są w ich ZPD.

Innym problemem jest to, że nadmierne upraszczanie daje nam fałszywe poczucie sukcesu. W tym przypadku pani Hartwell wierzyła, że jej uczniowie potrafią „zrobić matematykę” w zadaniu słownym. W rzeczywistości naśladowali oni tylko jej działania. Nie było powodu, by sądzić, że mogliby sami znaleźć podobne rozwiązanie.

Usunęła również cały proces „formułowania” z procesu rozwiązywania problemów. Wielu pedagogów uważa, że rozumienie i formułowanie to to samo, ale formułowanie jest odrębną kompetencją matematyczną.

And it may just be the missing ingredient from the way you currently teach word problems.

Classroom Resources and Professional Learning

Formulation: The Key to Success with Word Problems

Formułowanie problemów słownych wiąże się z ich zrozumieniem. Ale to wykracza poza to. Formułowanie jest bardziej jak tłumaczenie niż understanding.

Gdy uczeń czyta problem słowny, po pierwsze, muszą włączyć litery do dźwięków (dekodowania). Następnie, muszą zrozumieć, co oznaczają słowa (słownictwo). Musi zrozumieć, jak słowa pasują do siebie w zdaniu (składnia). Wreszcie, rozumienie pochodzi z połączenia tych elementów razem, aby nadać im znaczenie.

Większość uczniów szóstej klasy może przeczytać zadanie pani Hartwell i łatwo zrozumieć, że Sara rozdaje marchewki swoim koniom. Ale znacznie mniej osób połączy „dzielenie się” marchewkami z dzieleniem.

To jest ta część, która przeszkadza wielu nauczycielom. Dla nas wydaje się to takie oczywiste. „Ona dosłownie dzieli marchewki. Jak oni mogą nie widzieć, że to jest dzielenie?”.

Po prostu nie widzą. Gdyby tak było, nie widzielibyście tablic ze słowami kluczowymi wiszących w klasach matematycznych. A to wszystko wraca do czasów, kiedy po raz pierwszy uczymy operacji.

Dlaczego uczniowie zmagają się z formułowaniem pytań

Wielu nauczycieli w wielu szkołach uczy uczniów, że matematyka jest przedmiotem rozumowania. Ale w innych, matematyka jest nauczana jako przedmiot zapamiętywania.

Przykładem „matematyki jako zapamiętywania” jest sytuacja, gdy uczniowie zapamiętują fakty matematyczne. Ale algorytmy są również o zapamiętywaniu. Nałóż 120 na 47. Wykonaj te kroki, aby dodać, te, aby odjąć, a te, aby pomnożyć.

Uczniowie mogą powtarzać te kroki, nie rozumiejąc wielkości liczb, ani nawet tego, co oznaczają operacje.

Gdy zaczynamy od pojęć (używając modeli wizualnych lub zdań liczbowych), uczniowie uczą się, co oznaczają operacje. Kiedy przechodzimy od razu do algorytmu, uczniowie myślą o operacjach jako o serii przypadkowych kroków.

Rok po roku każemy uczniom zapamiętywać i powtarzać. Wykonują ten sam algorytm 30 razy na zadanie domowe. Zmień liczby, a proces pozostanie ten sam. Ale dajmy im problem słowny, a teraz muszą nadać mu sens.

Co testy mówią nam o rozumowaniu

Możemy dać naszym uczniom 10 problemów z tytułem „Problemy słowne z dzieleniem”, żeby było łatwiej. Nie będą musieli nawet czytać tych zadań. Muszą tylko odgadnąć (lub zgadnąć), która liczba jest dzielnikiem, a która dywidendą.

Ale kiedy uczniowie zasiadają do testu państwowego, celem nie jest uczynienie go łatwiejszym. Celem jest ocena tego, co mogą zrobić sami.

Testerzy nie chcą im mówić, jakiej operacji użyć. Umieszczają nawet słowa kluczowe dla dzielenia i dodawania w tym samym zadaniu. „W klasie jest 20 uczniów. Jeśli każde dziecko ma trzy dolary, to ile mają ich w sumie?”

Więc kiedy uczniowie zmagają się z problemami słownymi, to nie chodzi tylko o problemy ze słowami. Zazwyczaj oznacza to, że wykonują matematykę na pamięć. Musimy ich nauczyć, że matematyka polega na tworzeniu sensu.

Uczniowie potrzebują strategii i procesu do rozwiązywania zadań słownych

Częścią problemu z systemem takim jak CUBES jest to, że nazywa się on strategią, ale tak naprawdę jest procesem.

Proces to seria kroków. Kiedy już zidentyfikujesz efektywny proces, możesz go powtarzać wielokrotnie, nie zastanawiając się zbyt długo. Algorytmy są procesem. Podobnie jak ustawianie się w kolejce „od najwyższego do najniższego” na spacer na lunch.

Strategia jest inna. Strategie wymagają głębokiego zrozumienia. I zdolności do zastosowania tego zrozumienia w nowych sytuacjach.

Nie możemy przygotować uczniów na każdy scenariusz, jaki napotkają w zadaniach słownych. Niektóre z nich wymagają od nich połączenia różnych umiejętności matematycznych, których nigdy wcześniej nie łączyli. Mogą też wymagać od uczniów zmiany kolejności kroków, aby dojść do poprawnego rozwiązania.

Zastanów się nad następującą sytuacją:

Masz 5 galonów soku na imprezę szkolną z udziałem 100 uczniów. Jeśli każdy kubek ma pojemność 3 uncji, to ile kubków może wypić każdy uczeń? Ile jeszcze zostanie.

Proces rozwiązywania problemów może pomóc uczniom zacząć radzić sobie z tym problemem. „Zidentyfikuj, o co jest pytanie”. „Rozważ, jakie informacje są podawane.”

Ale nie ma ustalonego procesu, którego możemy ich nauczyć, aby faktycznie go rozwiązać. Tu pojawia się strategia. Muszą przeliczyć jednostki. Uznać, że dzielimy z resztami, a nie dzielimy całkowicie. Powinni też prawdopodobnie zmienić kolejność operacji, dzieląc sok na kubki przed dzieleniem przez liczbę uczniów.

Nie ma żadnej „sztuczki”, która doprowadzi uczniów do celu. Muszą oni zrozumieć znaczenie operacji. Muszą rozumieć matematykę jako przedmiot nadający sens. I muszą wielokrotnie ćwiczyć stosowanie myślenia strategicznego w zadaniach słownych.

Proces Polya do rozwiązywania zadań słownych

George Pólya był wpływowym węgierskim matematykiem i profesorem Stanfordu, który odkrył proces, który można wykorzystać do rozwiązania każdego problemu. Jego praca dotknęła niezliczonych matematyków i pedagogów, z których większość nie zna jego nazwiska.

W rzeczywistości, CUBES i inne tak zwane strategie rozwiązywania problemów są luźno oparte na jego pracy. Problem polega na tym, że próbują ją uprościć. W tym procesie usuwają wszystko, co przypomina głębokie myślenie.

Polya wierzył, że każdy problem może być rozwiązany w czterech krokach: Zrozum, Zaplanuj, Rozwiąż i Zastanów się. Myślę, że oryginalny czteroetapowy proces Polya’y jest w sam raz do zastosowania w szkołach.

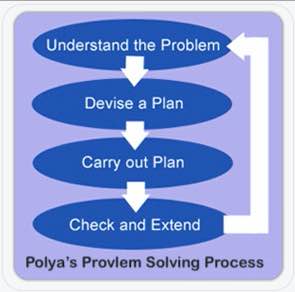Aby zrozumieć problem, określamy, jakie informacje są nam dane i co chcemy znaleźć. Stąd właśnie wzięły się „C” i „U” w kostkach. Jeśli uczniowie chcą zakreślać liczby i podkreślać pytanie, w porządku. Wolę jednak, aby zapisywali je (wraz z jednostkami) w organizerze graficznym, przynajmniej na początku. To pomaga im przetworzyć to, co czytają. Pomaga to również mnie, jako nauczycielowi, ocenić ich zrozumienie, gdy chodzę po sali.

Następna część jest trudna. Plan” to miejsce, w którym formułujemy problem. Bierzemy scenariusz świata rzeczywistego i przekształcamy go w inną matematyczną reprezentację.

Trzecim krokiem jest Rozwiązywanie. Jeśli poprawnie sformułowaliśmy problem, to właśnie tutaj dokonujemy obliczeń. Uczniowie zazwyczaj używają algorytmu, ale zachęcam do używania równań i modeli wizualnych, jak również.

Na koniec, uczniowie patrzą wstecz i sprawdzają swoją pracę. Powinni również zastanowić się nad swoim procesem. Jeśli popełniłem błąd, dlaczego? Czy ta strategia może mi pomóc w rozwiązywaniu podobnych problemów w przyszłości?

Strategie rozwiązywania zadań słownych

Posiadanie procesu podejścia do zadań słownych jest zdecydowanie pomocne. Ale nie możemy udawać, że sensownej matematyki można się nauczyć tylko poprzez podążanie za krokami. Cały sens problemów słownych polega na rozszerzeniu matematyki poza „fakty matematyczne” i algorytmy.

Istnieją pewne pomocne strategie, aby pomóc uczniom w formułowaniu. Na początku wyraźnie uczę kilku różnych strategii.

W miarę jak uczę strategii, każę uczniom rozwiązywać zadania, które dobrze pasują do danej strategii. Niektóre typy problemów bardzo dobrze współgrają z „Zgaduj i sprawdzaj”. Inne są bardziej odpowiednie dla 'Narysuj obrazek’.

W końcu daję im trudne zadania słowne, które mogą być rozwiązane na kilka sposobów. Kiedy mają już narzędzia w swoich paskach narzędzi, mogą wybrać, który jest najlepszy dla danej sytuacji.

Połączenie strategii może być również bardzo skuteczne. Na przykład, rysowanie obrazu może być często pomocne w formułowaniu myśli. Jeśli rolnik ma 18 rzędów marchwi i 10 marchewek w każdym rzędzie, uczeń może zacząć od narysowania pola. W pewnym momencie może pomyśleć „Wow, to jest tablica” i zdać sobie sprawę, że może mnożyć używając matematyki mentalnej, wyrażenia lub algorytmu.

Innym razem uczniowie mogą użyć modeli wizualnych do sformułowania i rozwiązania problemu.

Pomóż uczniom uporać się z trudnymi zadaniami

Jeśli jesteś jak wielu nauczycieli, możesz się martwić, jak twoi uczniowie poradzą sobie z tym wszystkim. Procesy, strategie, krytyczne myślenie… jest w to zaangażowane bardzo wiele.

Może nawet myślisz, że przed tym artykułem zadania słowne wydawały się łatwiejsze. Jeśli tak, to przepraszam.

Kluczem jest, aby nie dać się przytłoczyć próbując zrobić wszystko na raz. Zacznij od rozwiązania prostego zadania słownego, stosując proces Polya’y. Następnie, co tydzień wprowadzaj nową strategię. Pod koniec roku będziesz zdumiony, jak daleko zaszli.

Może jesteś zainteresowany pogłębieniem kreatywnego rozwiązywania problemów. Rozważ uczestnictwo w praktycznych warsztatach matematycznych lub pracę z trenerem online.

Jeśli jesteś gotowy, aby wprowadzić jutro do swojej klasy program Polya, ten organizer graficzny jest świetnym sposobem, aby zacząć. Ułatwi on przejście przez czterostopniowy proces i pomoże zidentyfikować, gdzie uczniowie zbaczają z kursu.

Free Word Problem Organizer

About the Author

Jeff Lisciandrello jest założycielem Room to Discover i konsultantem edukacyjnym specjalizującym się w nauczaniu skoncentrowanym na uczniu. Jego 3-Bridges Design for Learning pomaga szkołom w odkrywaniu innowacyjnych praktyk w tradycyjnych warunkach. Lubi pomagać nauczycielom w przyjęciu podejścia do nauczania opartego na dociekaniu i personalizacji. Możesz połączyć się z nim poprzez Twitter @EdTechJeff

.