Introductory Business Statistics

Rozważmy następujący zbiór danych.
4; 5; 6; 6; 6; 7; 7; 7; 7; 7; 7; 8; 8; 8; 9; 10

Ten zestaw danych może być reprezentowany przez następujący histogram. Każdy przedział ma szerokość jeden, a każda wartość znajduje się w środku przedziału.

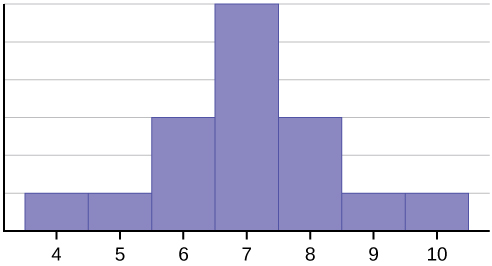
Histogram przedstawia symetryczny rozkład danych. Rozkład jest symetryczny, jeśli w pewnym punkcie histogramu można narysować pionową linię, która sprawia, że kształty po lewej i prawej stronie pionowej linii są lustrzanymi odbiciami siebie nawzajem. Średnia, mediana i tryb są po siedem dla tych danych. W idealnie symetrycznym rozkładzie, średnia i mediana są takie same. Ten przykład ma jeden tryb (jednomodalny), a tryb jest taki sam jak średnia i mediana. W symetrycznym rozkładzie, który ma dwa tryby (bimodalny), te dwa tryby byłyby różne od średniej i mediany.

Histogram dla danych: 4566677778 nie jest symetryczny. Prawa strona wydaje się „obcięta” w stosunku do lewej. Rozkład tego typu nazywamy skośnym w lewo, ponieważ jest on wyciągnięty w lewo. Możemy formalnie zmierzyć skośność rozkładu, tak samo jak możemy matematycznie zmierzyć wagę środka danych lub ich ogólną „szparowatość”. Wzór matematyczny na skośność to: . Im większe odchylenie od zera wskazuje na większy stopień skośności. Jeśli skośność jest ujemna, wówczas rozkład jest przechylony w lewo, jak na rysunku (rysunek). Dodatnia miara skośności wskazuje na skośność prawostronną, jak w przypadku (rysunek).

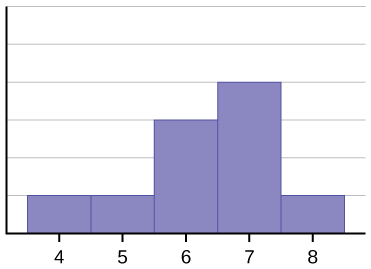
Średnia wynosi 6,3, mediana 6,5, a tryb siedem. Zauważ, że średnia jest mniejsza niż mediana, a oba są mniejsze niż tryb. Zarówno średnia jak i mediana odzwierciedlają skośność, ale średnia odzwierciedla ją bardziej.

Histogram dla danych: 67777888910, również nie jest symetryczny. Jest pochylony w prawo.

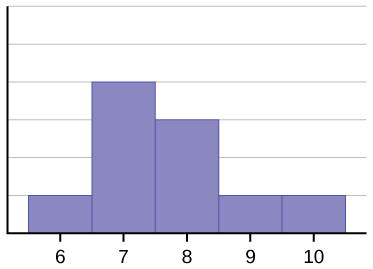
Średnia wynosi 7,7, mediana 7,5, a tryb siedem. Z tych trzech statystyk, średnia jest największa, podczas gdy tryb jest najmniejszy. Ponownie, średnia odzwierciedla skośność najbardziej.

Podsumowując, ogólnie jeśli dystrybucja danych jest skośna w lewo, średnia jest mniejsza niż mediana, która jest często mniejsza niż tryb. Jeśli dystrybucja danych jest skośna w prawo, tryb jest często mniej niż mediana, która jest mniejsza niż średnia.

Jak ze średnią, medianą i trybem, i jak zobaczymy wkrótce, wariancja, istnieją wzory matematyczne, które dają nam dokładne środki tych cech dystrybucji danych. Ponownie patrząc na wzór na skośność widzimy, że jest to relacja między średnią danych a poszczególnymi obserwacjami sześciennymi.

gdzie jest przykładowym odchyleniem standardowym danych, , a jest średnią arytmetyczną i jest wielkością próby.

Formalnie średnia arytmetyczna jest znana jako pierwszy moment rozkładu. Drugim momentem, który zobaczymy, jest wariancja, a skośność jest trzecim momentem. Wariancja mierzy kwadratowe różnice danych w stosunku do średniej, a skośność mierzy sześcienne różnice danych w stosunku do średniej. Podczas gdy wariancja nigdy nie może być liczbą ujemną, miara skośności może i w ten sposób określamy, czy dane są skośne w prawo czy w lewo. Skośność dla rozkładu normalnego wynosi zero, a wszelkie dane symetryczne powinny mieć skośność bliską zeru. Ujemne wartości dla skośności wskazują na dane, które są przechylone w lewo, a dodatnie wartości dla skośności wskazują na dane, które są przechylone w prawo. Przez skośność w lewo rozumiemy, że lewy ogon jest długi w stosunku do prawego ogona. Analogicznie, skośność w prawo oznacza, że prawy ogon jest długi w stosunku do lewego ogona. Skośność charakteryzuje stopień asymetrii rozkładu wokół jego średniej. O ile średnia i odchylenie standardowe są wielkościami wymiarowymi (dlatego będziemy brać pierwiastek kwadratowy z wariancji), czyli mają te same jednostki co wielkości mierzone , o tyle skośność jest umownie zdefiniowana w taki sposób, że nie jest wielowymiarowa. Jest to liczba czysta, charakteryzująca jedynie kształt rozkładu. Dodatnia wartość skośności oznacza rozkład z asymetrycznym ogonem, który rozciąga się w kierunku bardziej dodatniego X, a ujemna wartość oznacza rozkład, którego ogon rozciąga się w kierunku bardziej ujemnego X. Zerowa miara skośności oznacza rozkład symetryczny.

Skośność i symetria stają się ważne, gdy omawiamy rozkłady prawdopodobieństwa w późniejszych rozdziałach.

.