The Toom-Cook Algorithm
Tutaj uczymy się pomysłowego zastosowania algorytmu dziel i zwyciężaj w połączeniu z algebrą liniową do mnożenia dużych liczb, szybko. Oraz wprowadzenie do notacji Big-O!
W rzeczywistości ten wynik jest tak sprzeczny z intuicją, że wielki matematyk Kołmogorow przypuszczał, że tak szybki algorytm nie istnieje.
Part 0: Long Multiplication is Slow Multiplication. (I wprowadzenie do notacji Big-O)
Wszyscy pamiętamy naukę mnożenia w szkole. W rzeczywistości, muszę się do tego przyznać. Pamiętajcie, to jest strefa bez oceniania 😉
W szkole mieliśmy 'mokrą zabawę’, kiedy deszcz padał zbyt mocno, aby bawić się na placu zabaw. Podczas gdy inne (normalne/lubiące zabawę/pozytywny przymiotnik do wyboru) dzieci grały w gry i wygłupiały się, ja czasami brałem kartkę papieru i mnożyłem razem duże liczby, tak dla samej przyjemności. Czysta radość z obliczeń! Mieliśmy nawet konkurs mnożenia, „Super 144”, w którym musieliśmy pomnożyć zakodowaną siatkę 12 na 12 liczb (od 1 do 12) w jak najkrótszym czasie. Ćwiczyłem to religijnie, do tego stopnia, że miałem swoje własne przygotowane arkusze ćwiczeniowe, które kserowałem, a następnie używałem na zmianę. W końcu osiągnąłem czas 2 minut i 1 sekundy, przy którym mój fizyczny limit bazgrania został osiągnięty.
Mimo tej obsesji na punkcie mnożenia, nigdy nie przyszło mi do głowy, że moglibyśmy to robić lepiej. Spędziłem tak wiele godzin na mnożeniu, ale nigdy nie próbowałem ulepszyć algorytmu.
Rozważmy mnożenie 103 przez 222.
Obliczamy 2 razy 3 razy 1 +2 razy 0 razy 10 + 2 razy 1 razy 100 + 20 razy 3 razy 1 + 20 razy 0 razy 10 + 20 razy 1 razy 100 = 22800
Ogólnie, aby pomnożyć n cyfr, potrzeba O(n²) operacji. Notacja 'big-O’ oznacza, że gdybyśmy mieli wykreślić wykres liczby operacji jako funkcji n, termin n² jest naprawdę tym, co się liczy. Kształt jest zasadniczo kwadratowy.
Dzisiaj spełnimy wszystkie nasze dziecięce marzenia i udoskonalimy ten algorytm. Ale najpierw! Czeka nas Big-O.
Big-O
Spójrz na dwa wykresy poniżej

Zapytaj matematyka, „czy x² i x²+x^(1/3) są takie same?”, a prawdopodobnie zwymiotuje do swojej filiżanki z kawą, zacznie płakać i mamrotać coś o topologii. Przynajmniej taka była moja reakcja (na początku), a ja prawie nic nie wiem o topologii.
Ok. To nie jest to samo. Ale nasz komputer nie dba o topologię. Komputery różnią się wydajnością na tak wiele sposobów, których nawet nie potrafię opisać, bo nic nie wiem o komputerach.
Ale nie ma sensu dostrajać walca parowego. Jeśli dwie funkcje, dla dużych wartości ich danych wejściowych, rosną w tym samym rzędzie wielkości, to dla celów praktycznych zawiera to większość istotnych informacji.
Na powyższym wykresie widzimy, że te dwie funkcje wyglądają dość podobnie dla dużych danych wejściowych. Ale podobnie, x² i 2x² są podobne – ta druga jest tylko dwa razy większa od pierwszej. Przy x = 100, jeden jest 10 000, a drugi 20 000. Oznacza to, że jeśli możemy obliczyć jedną, prawdopodobnie możemy obliczyć drugą. Natomiast funkcja, która rośnie wykładniczo, powiedzmy 10^x, przy x = 100 jest już o wiele większa niż liczba atomów we wszechświecie. (10¹⁰⁰ >>>> 10⁸⁰, co jest szacunkową liczbą Eddingtona na temat liczby atomów we wszechświecie według mojego Googlowania*).
*prawdę mówiąc, użyłem DuckDuckGo.
Pisanie liczb całkowitych jako wielomianów jest zarówno bardzo naturalne, jak i bardzo nienaturalne. Napisanie 1342 = 1000 + 300 + 40 + 2 jest bardzo naturalne. Zapisanie 1342 = x³+3x²+4x + 2, gdzie x = 10, jest nieco dziwne.
W ogólności, załóżmy, że chcemy pomnożyć dwie duże liczby, zapisane w podstawie b, o n cyfrach każda. Każdą n-cyfrową liczbę zapisujemy jako wielomian. Jeśli podzielimy liczbę n-cyfrową na r części, to wielomian ten ma n/r wyrazów.
Na przykład, niech b = 10, r = 3, a nasza liczba to 142,122,912
Możemy to przekształcić w
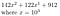
To działa bardzo ładnie, gdy r = 3, a nasza liczba, zapisana w podstawie 10, miała 9 cyfr. Jeśli r nie dzieli idealnie n, to możemy po prostu dodać kilka zer z przodu. Ponownie, najlepiej zilustruje to przykład.
27134 = 27134 + 0*10⁵ = 027134, który przedstawiamy jako
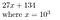
Dlaczego to może być pomocne? Aby znaleźć współczynniki wielomianu P, jeśli wielomian jest rzędu N, to próbkując go w N+1 punktach możemy wyznaczyć jego współczynniki.
Na przykład, jeśli wielomian x⁵ + 3x³ +4x-2, który jest rzędu 5, spróbkujemy w 6 punktach, to możemy wtedy rozpracować cały wielomian.
Intuicyjnie wielomian rzędu 5 ma 6 współczynników: współczynnik 1, x, x², x³, x⁴, x⁵. Biorąc pod uwagę 6 wartości i 6 niewiadomych, możemy znaleźć te wartości.
(Jeśli znasz algebrę liniową, możesz potraktować różne potęgi x jako wektory liniowo niezależne, utworzyć macierz reprezentującą informacje, odwrócić macierz i voila)
Próbkowanie wielomianów w celu określenia współczynników (Opcjonalnie)
Tutaj przyjrzymy się nieco bardziej szczegółowo logice stojącej za próbkowaniem wielomianu w celu wydedukowania jego współczynników. Nie krępuj się przejść do następnej sekcji.
Pokażemy, że jeśli dwa wielomiany stopnia N zgadzają się w N+1 punktach, to muszą być takie same. Tzn. N+1 punktów jednoznacznie określa wielomian rzędu N.
Rozważmy wielomian rzędu 2. Jest on postaci P(z) = az² +bz + c. Zgodnie z fundamentalnym twierdzeniem algebry – bezwstydnie, wtyczka tutaj, spędziłem kilka miesięcy, składając dowód tego, a następnie pisząc go, tutaj – ten wielomian może być faktoryzowany. To oznacza, że możemy go zapisać jako A(z-r)(z-w)
Zauważmy, że przy z = r, oraz przy z = w, wielomian jest obliczany na 0. Mówimy, że w i r są korzeniami wielomianu.
Teraz pokażemy, że P(z) nie może mieć więcej niż dwa korzenie. Załóżmy, że ma on trzy korzenie, które nazywamy w, r, s. Następnie dokonujemy faktoryzacji wielomianu. P(z) = A(z-r)(z-w). Następnie P(s) = A(s-r)(s-w). Nie jest to równe 0, gdyż mnożąc liczby niezerowe otrzymujemy liczbę niezerową. Jest to sprzeczność, gdyż naszym pierwotnym założeniem było, że s jest pierwiastkiem wielomianu P.
Ten argument można zastosować do wielomianu rzędu N w zasadniczo identyczny sposób.
Załóżmy teraz, że dwa wielomiany P i Q rzędu N zgadzają się w N+1 punktach. Wtedy, jeśli są różne, to P-Q jest wielomianem rzędu N, który w N+1 punktach jest równy 0. Z poprzedniego założenia wynika, że jest to niemożliwe, gdyż wielomian rzędu N ma co najwyżej N pierwiastków. Zatem nasze założenie musiało być błędne, a jeśli P i Q zgadzają się w N+1 punktach to są tym samym wielomianem.
Seeing is believing: A Worked Example
Przyjrzyjrzyjmy się naprawdę ogromnej liczbie, którą nazwiemy p. W bazie 10, p ma długość 24 cyfr (n=24) i podzielimy ją na 4 części (r=4). n/r = 24/4 = 6
p = 292,103,243,859,143,157,364,152.
A reprezentujący go wielomian niech się nazywa P,
P(x) = 292,103 x³ + 243,859 x² +143,157 x+ 364,152
z P(10⁶) = p.
Ponieważ stopień tego wielomianu jest równy 3, możemy wszystkie współczynniki wyznaczyć z próbkowania w 4 miejscach. Zobaczmy, co się stanie, gdy spróbkujemy go w kilku punktach.
- P(0) = 364,152
- P(1) = 1,043,271
- P(-1) = 172,751
- P(2) = 3,962,726
Uderzające jest to, że wszystkie one mają 6 lub 7 cyfr. To w porównaniu z 24 cyframi występującymi pierwotnie w p.
Mnóżmy p przez q. Niech q = 124,153,913,241,143,634,899,130, i
Q(x) = 124,153 x³ + 913,241 x²+143,634 x + 899,130
Obliczanie t=pq może być straszne. Ale zamiast robić to bezpośrednio, spróbujemy obliczyć wielomianową reprezentację t, którą oznaczymy T. Ponieważ P jest wielomianem rzędu r-1=3, a Q jest wielomianem rzędu r-1 = 3, T jest wielomianem rzędu 2r-2 = 6.
T(10⁶) = t = pq
T(10⁶) = P(10⁶)Q(10⁶)
Sztuczka polega na tym, że będziemy obliczać współczynniki T, a nie bezpośrednio mnożyć p i q razem. Wówczas obliczenie T(1⁰⁶) jest proste, bo aby pomnożyć przez 1⁰⁶ wystarczy dopisać 6 zer z tyłu. Sumowanie wszystkich części jest również łatwe, ponieważ dodawanie jest bardzo tanim działaniem, które mogą wykonywać komputery.
Aby obliczyć współczynniki T, musimy pobrać próbki w 2r-1 = 7 punktach, ponieważ jest to wielomian rzędu 6. Prawdopodobnie chcemy wybrać małe liczby całkowite, więc wybieramy
- T(0)=P(0)Q(0)= 364,152*899,130
- T(1)=P(1)Q(1)= 1,043,271*2,080,158
- T(2)=P(2)Q(2)= 3,962,726*5,832,586
- T(-1)=P(-1)Q(-1)= 172751*1544584
- T(-2)=P(-2)Q(-2)= -1,283,550*3,271,602
- T(3)=P(-3)Q(-3)= -5,757,369*5,335,266
Uwaga na wielkość liczb P(-3), Q(-3), P(2), Q(2) itd…. Wszystkie te liczby mają w przybliżeniu n/r = 24/4 = 6 cyfr. Niektóre z nich mają 6 cyfr, niektóre 7. W miarę jak n staje się większe, to przybliżenie staje się coraz bardziej rozsądne.
Do tej pory zredukowaliśmy problem do następujących kroków, lub algorytmu:
(1) Najpierw oblicz P(0), Q(0), P(1), Q(1), itd (działanie o niskim koszcie)
(2) Aby otrzymać nasze 2r-1= 7 wartości T(x), musimy teraz pomnożyć 2r-1 liczb o przybliżonym rozmiarze n/r cyfr długości. Mianowicie, musimy obliczyć P(0)Q(0), P(1)Q(1), P(-1)Q(-1), itd. (Wysoki koszt działania)
(3) Zrekonstruuj T(x) z naszych punktów danych. (Działanie niskokosztowe: ale będzie rozważane później).
(4) Z naszym zrekonstruowanym T(x), oceń T(10⁶) w tym przypadku
To ładnie prowadzi do analizy czasu działania tego podejścia.
Czas działania
Z powyższego dowiedzieliśmy się, że chwilowo ignorując działania o niskim koszcie (1) i (3), koszt mnożenia dwóch n-cyfrowych liczb algorytmem Tooma będzie zgodny z:
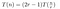
To właśnie widzieliśmy w działającym przykładzie. Pomnożenie każdej liczby P(0)Q(0), P(1)Q(1) itd. kosztuje T(n/r), bo mnożymy dwie liczby o długości około n/r. Musimy to zrobić 2r-1 razy, ponieważ chcemy pobrać próbkę T(x) – będącą wielomianem rzędu 2r-2 – w 2r-1 miejscach.
Jak szybkie to jest? Możemy rozwiązać tego typu równanie w sposób jawny.

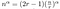
Teraz pozostaje nam tylko trochę niechlujna algebra
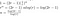
Jako, że było kilka innych kosztów z procesu mnożenia macierzy („ponownego składania”), i z dodawania, nie możemy powiedzieć, że nasze rozwiązanie jest dokładnym czasem działania, więc zamiast tego stwierdzamy, że znaleźliśmy big-O czasu działania
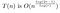
Optymalizacja r
Ten czas działania nadal zależy od r. Poprawiamy r i kończymy. Ale nasza ciekawość nie jest jeszcze zaspokojona!
Jak n staje się duże, chcemy znaleźć w przybliżeniu optymalną wartość dla naszego wyboru r. Tzn. chcemy wybrać wartość r, która zmienia się dla różnych wartości n.
Kluczową rzeczą jest to, że przy zmieniającym się r, musimy zwrócić uwagę na koszt ponownego złożenia – macierz, która wykonuje tę operację ma koszt O(r²). Kiedy r było stałe, nie musieliśmy na to patrzeć, ponieważ gdy n rosło duże przy stałym r, to warunki obejmujące n określały wzrost tego, ile obliczeń było wymaganych. Ponieważ nasz optymalny wybór r będzie się zwiększał wraz ze wzrostem n, nie możemy już tego ignorować.
To rozróżnienie jest kluczowe. Początkowo nasza analiza wybrała wartość r, być może 3, być może 3 miliardy, a następnie przyjrzeliśmy się rozmiarowi big-O, gdy n rosło arbitralnie duże. Teraz, patrzymy na zachowanie jak n rośnie arbitralnie duże i r rośnie z n w jakimś tempie, które określamy. Ta zmiana perspektywy patrzy na O(r²) jak na zmienną, podczas gdy kiedy r było utrzymywane na stałym poziomie, O(r²) było stałą, aczkolwiek taką, której nie znaliśmy.
Zaktualizujemy więc naszą analizę sprzed lat:
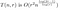
gdzie O(r²) reprezentuje koszt macierzy ponownego składania. Chcemy teraz wybrać taką wartość r dla każdej wartości n, która w przybliżeniu minimalizuje to wyrażenie. Aby zminimalizować, najpierw próbujemy różniczkować względem r. Daje to nieco ohydnie wyglądające wyrażenie

Normalnie, aby znaleźć punkt minimalny, ustawiamy pochodną równą 0. Ale to wyrażenie nie ma ładnego minimum. Zamiast tego znajdujemy „wystarczająco dobre” rozwiązanie. Używamy r = r^(sqrt(logN)) jako naszej wartości przybliżonej. Graficznie, jest to całkiem blisko minimum. (Na wykresie poniżej, współczynnik 1/1000 jest po to, aby wykres był widoczny w rozsądnej skali)
Wykres poniżej pokazuje naszą funkcję dla T(N), skalowaną przez stałą, w kolorze czerwonym. Zielona linia znajduje się przy x = 2^sqrt(logN), co było naszą wartością przybliżoną. 'x’ zajmuje miejsce 'r’, a na każdym z trzech obrazków użyta jest inna wartość N.



To jest dla mnie dość przekonujące, że nasz wybór był dobry. Z tym wyborem r, możemy go podłączyć i zobaczyć jak wygląda końcowy big-O naszego algorytmu:

gdzie po prostu podłączyliśmy naszą wartość dla r, i użyliśmy przybliżenia dla log(2r-1)/log(r), które jest bardzo dokładne dla dużych wartości r.
How Much of An Improvement?
Może to, że nie zauważyłem tego algorytmu, gdy byłem małym chłopcem wykonującym mnożenie, było rozsądne. Na poniższym wykresie podaję, że współczynnik naszej funkcji Big-O wynosi 10 (w celach demonstracyjnych) i dzielę go przez x² (ponieważ oryginalne podejście do mnożenia było O(n²)). Jeśli czerwona linia ma tendencję do 0, pokazałoby to, że nasz nowy czas działania asymptotycznie jest lepszy niż O(n²).
I rzeczywiście, podczas gdy kształt funkcji pokazuje, że nasze podejście jest ostatecznie szybsze, a ostatecznie jest znacznie szybsze, musimy poczekać, aż będziemy mieli prawie 400 cyfr długich liczb, aby tak się stało! Nawet jeśli współczynnik wynosiłby tylko 5, liczby musiałyby mieć około 50 cyfr długości, aby zobaczyć poprawę prędkości.

Dla mojego 10-letniego ja, mnożenie 400-cyfrowych liczb byłoby trochę naciągane! Śledzenie różnych rekursywnych wywołań mojej funkcji również byłoby nieco zniechęcające. Ale dla komputera wykonującego zadania w AI lub w fizyce, jest to powszechny problem!
Jak głęboki jest ten wynik?
To, co kocham w tej technice, to fakt, że nie jest to rocket science. Nie jest to najbardziej skomplikowana matematyka, jaka kiedykolwiek została odkryta. Z perspektywy czasu, być może wydaje się to oczywiste!
Ale to jest właśnie błyskotliwość i piękno matematyki. Czytałem, że Kołmogorow przypuszczał na seminarium, że mnożenie jest zasadniczo O(n²). Kołmogorow w zasadzie wymyślił wiele z nowoczesnej teorii prawdopodobieństwa i analizy. Był jednym z wielkich matematyków XX wieku. Jednak gdy przyszło do tej niezwiązanej z nim dziedziny, okazało się, że istniał cały korpus wiedzy czekający na odkrycie, siedzący tuż pod nosem jego i wszystkich innych!
W rzeczywistości algorytmy Divide and Conquer dość szybko przychodzą dziś na myśl, ponieważ są tak powszechnie używane. Ale są one produktem rewolucji komputerowej, ponieważ dopiero dzięki ogromnej mocy obliczeniowej ludzkie umysły skupiły się na szybkości obliczeń jako dziedzinie matematyki wartej samodzielnego studiowania.
To dlatego matematycy nie są skłonni zaakceptować Hipotezy Riemanna jako prawdziwej tylko dlatego, że wydaje się, iż może być prawdziwa, albo że P nie jest równe NP tylko dlatego, że wydaje się to najbardziej prawdopodobne. Cudowny świat matematyki zawsze zachowuje zdolność do dezorientowania naszych oczekiwań.
W rzeczywistości, można znaleźć jeszcze szybsze sposoby mnożenia. Najlepsze obecnie podejścia wykorzystują szybkie transformaty Fouriera. Ale zachowam to na inny dzień 🙂
Pozwól mi poznać swoje myśli poniżej. Jestem nowo na Twitterze jako ethan_the_mathmo, możesz mnie śledzić tutaj.
Natknąłem się na ten problem we wspaniałej książce, której używam, zwanej „The Nature of Computation” autorstwa fizyków Moore’a i Mertensa, gdzie jeden z problemów prowadzi cię przez analizę algorytmu Tooma.