Posted on 29 listopada 2018 by Maximilian Siebert
Heterogeniczność nie jest czymś, czego należy się bać, oznacza po prostu, że w Twoich danych występuje zmienność. Tak więc, jeśli ktoś zbiera różne badania w celu ich przeanalizowania lub przeprowadzenia metaanalizy, jest oczywiste, że zostaną znalezione różnice. Przeciwieństwem heterogeniczności jest homogeniczność, co oznacza, że wszystkie badania wykazują ten sam efekt.
Ważne jest, aby zauważyć, że istnieją różne rodzaje heterogeniczności:
- Kliniczna: Różnice w uczestnikach, interwencjach lub wynikach
- Metodologiczna: Różnice w projekcie badania, ryzyko błędu systematycznego
- Statystyczna: Variation in intervention effects or results
Interesują nas te różnice, ponieważ mogą one wskazywać, że nasza interwencja może nie działać w ten sam sposób za każdym razem, gdy jest stosowana. Badając te różnice, można lepiej zrozumieć, jakie czynniki wpływają na interwencję i jakich wyników można się spodziewać przy następnym wdrożeniu interwencji.
Chociaż niejednorodność kliniczna i metodologiczna są ważne, na tym blogu skupimy się na niejednorodności statystycznej.
Jak zidentyfikować i zmierzyć niejednorodność
Test oka
W swoim wykresie leśnym zwróć uwagę na nakładające się przedziały ufności, a nie na to, po której stronie znajdują się oszacowania efektów. To, czy wyniki znajdują się po obu stronach linii braku efektu, może nie wpłynąć na twoją ocenę, czy heterogeniczność jest obecna, ale może wpłynąć na twoją ocenę, czy heterogeniczność ma znaczenie.
Mając to na uwadze, spójrz na poniższy wykres i zdecyduj, która działka jest bardziej jednorodna.
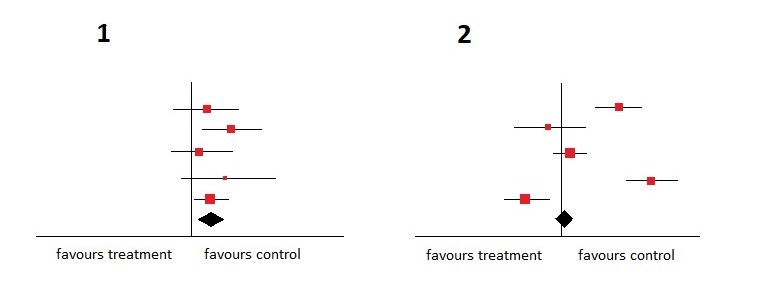
Oczywiście, bardziej jednorodna jest działka numer 1 . Przedziały ufności nakładają się na siebie, a ponadto wszystkie badania faworyzują interwencję kontrolną.
Dla ludzi, którzy uwielbiają mierzyć rzeczy, a nie tylko patrzeć im w oczy, nie martwcie się, nadal istnieją pewne metody statystyczne, które pomogą wam uchwycić koncepcję heterogeniczności.
Test Chi-squared (χ²)
Test ten zakłada hipotezę zerową, że wszystkie badania są homogeniczne, lub że każde badanie mierzy identyczny efekt, i daje nam wartość p do przetestowania tej hipotezy. Jeśli wartość p testu jest niska, możemy odrzucić hipotezę i heterogeniczność jest obecna.
Ponieważ test często nie jest wystarczająco czuły, a błędne wykluczenie heterogeniczności następuje szybko, wielu naukowców używa wartości p < 0,1 zamiast < 0,05 jako odcięcia.
I²
Test ten został opracowany przez profesora Juliana Higginsa i ma teorię pomiaru zakresu heterogeniczności, a nie stwierdzenia, czy jest ona obecna, czy nie.
Progi interpretacji I² mogą być mylące, ponieważ znaczenie niespójności zależy od kilku czynników. Przybliżony przewodnik interpretacji jest następujący:
- 0% do 40%: może nie mieć znaczenia
- 30% do 60%: umiarkowana heterogeniczność
- 50% do 90%: znaczna heterogeniczność
- 75% do 100%: znaczna heterogeniczność
Aby zrozumieć powyższą teorię spójrz na następujący przykład.
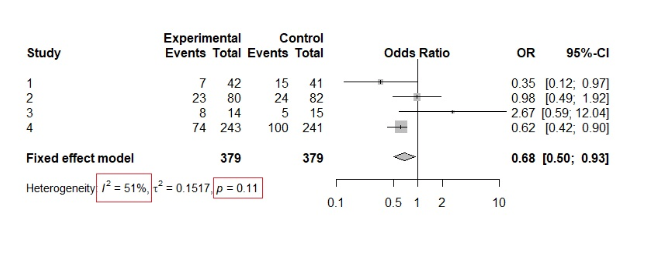
Widzimy, że wartość p testu chi kwadrat wynosi 0,11, potwierdzając hipotezę zerową, a tym samym sugerując homogeniczność. Jednakże, patrząc na interwencje, możemy już dostrzec pewną heterogeniczność wyników. Ponadto wartość I² wynosi 51%, co sugeruje umiarkowaną lub znaczną heterogeniczność.
Jest to dobry przykład tego, jak test χ² może być mylący, gdy w metaanalizie znajduje się tylko kilka badań.
Jak radzić sobie z heterogenicznością?
Po wykryciu zmienności w wynikach należy sobie z nią poradzić. Oto kilka kroków, jak poradzić sobie z tym problemem:
- Sprawdź swoje dane pod kątem błędów – Wróć i sprawdź, czy może wpisałeś coś nie tak
- Nie rób metaanalizy, jeśli heterogeniczność jest zbyt duża – Nie każdy przegląd systematyczny wymaga metaanalizy
- Zbadaj heterogeniczność – Można to zrobić za pomocą analizy podgrup lub meta-regresji
- Przeprowadź metaanalizę efektów losowych – Należy pamiętać, że to podejście dotyczy heterogeniczności, której nie można wyjaśnić, ponieważ jest spowodowana przypadkiem
- Zmień miary efektu – Powiedzmy, że używasz Różnicy ryzyka i masz wysoką heterogeniczność, to wypróbuj Risk Ratio lub Odds Ratio
(1) Fletcher, J. Co to jest heterogeniczność i czy jest ważna? BMJ 2007; 334 :94
(2) Deeks JJ, Higgins JPT, Altman DG (redaktorzy). Chapter 9: Analysing data and undertaking meta-analyses. In: Higgins JPT, Green S (redaktorzy). Cochrane Handbook for Systematic Reviews of Interventions Version 5.1.0 . The Cochrane Collaboration, 2011. Dostępne pod adresem www.cochrane-handbook.org.
(3) https://www.mathsisfun.com/data/chi-square-test.html
.