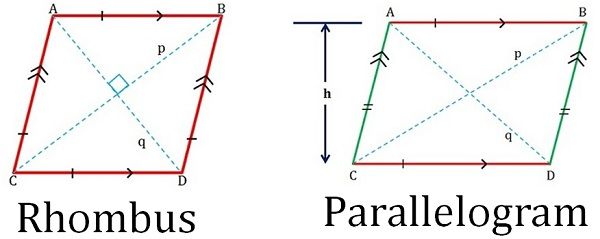
W geometrii, istnieje wiele rodzajów czworokątów tj. równoległobok, romb, kwadrat, prostokąt, trapez i latawiec, które mają wspólne cechy, z powodu których ludzie napotykają problemy w zrozumieniu tych figur. Romb może być określany jako pochylony kwadrat, którego sąsiednie boki są równe. Przeciwnie, równoległobok jest pochyłym prostokątem z dwoma zestawami równoległych przeciwległych boków.
Podstawowa różnica między rombem i równoległobokiem leży w ich właściwościach, tj. wszystkie boki rombu mają tę samą długość, podczas gdy równoległobok jest figurą prostoliniową, której przeciwległe boki są równoległe.
Zawartość: Rhombus Vs Parallelogram
- Comparison Chart
- Definition
- Key Differences
- Conclusion
Comparison Chart
.
| Podstawa porównania | Rhombus | Parallelogram |
|---|---|---|
| Znaczenie | Rhombus odnosi się do płasko ukształtowanej, czterobocznej figury, której wszystkie boki są przystające. | Równoległobok to figura płaska o czterech bokach, której przeciwległe boki są do siebie równoległe. |
| Równe boki | Wszystkie cztery boki mają równą długość. | |
| Krzyżówki | Krzyżówki przecinają się pod kątem prostym tworząc trójkąt skalenny. | Krzyżówki przecinają się tworząc dwa trójkąty przystające. |
| Powierzchnia | (pq)/2, gdzie p i q są przekątnymi | bh, gdzie b = podstawa i h = wysokość |
| Perymetr | 4 a, gdzie a = bok | 2 (a+b), gdzie a = bok, b = podstawa |
Definicja rombu
Czworokąt, którego długości boków są przystające nazywamy rombem. Ma on płaski kształt i cztery boki, przy czym zwrócone do siebie boki są do siebie równoległe (patrz rysunek poniżej).
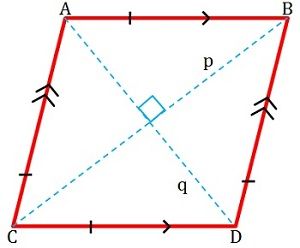Kąty przeciwległe rombu są równe, tzn. tego samego stopnia. Jego przekątne spotykają się pod kątem 90 stopni (kąt prosty), a więc są do siebie prostopadłe i tworzą dwa trójkąty równoboczne. Jego sąsiednie boki są komplementarne, co oznacza, że suma ich miar jest równa 180 stopni. Jest również znany jako równoległobok równoboczny.
Definicja równoległoboku
Równoległobok, jak sama nazwa wskazuje, jest opisywany jako figura o płaskim kształcie, posiadająca cztery boki, których zestaw przeciwległych boków jest równoległy i przystający (patrz rysunek poniżej).
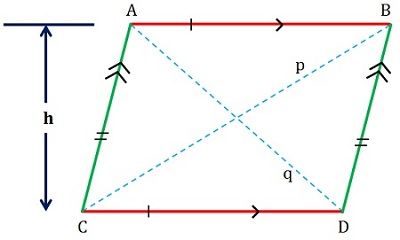Miara jego kątów skierowanych jest równa, a kolejne kąty są uzupełniające, tzn. suma ich miar jest równa 180 stopni. Jego przekątne przecinają się, tworząc dwa przystające trójkąty.
Kluczowe różnice między rombem a równoległobokiem
Różnice między rombem a równoległobokiem mogą być jasno określone na następujących podstawach:
- Romb definiujemy jako czworokąt o płaskim kształcie, którego wszystkie długości boków są przystające. Równoległobok to czworokąt o płaskim kształcie, którego przeciwległe boki są do siebie równoległe.
- Wszystkie boki rombu są równej długości, podczas gdy tylko przeciwległe boki równoległoboku są równe.
- Krzyżówki rombu przecinają się pod kątem prostym tworząc dwa trójkąty skalene. W przeciwieństwie do równoległoboku, którego przekątne przecinają się tworząc dwa trójkąty przystające.
- Wzór matematyczny na pole rombu to (pq)/2, gdzie p i q są przekątnymi. I odwrotnie, pole równoległoboku może być obliczone przez pomnożenie podstawy i wysokości.
- Obwód rombu może być obliczony za pomocą następującego wzoru – 4 a, gdzie a = bok rombu. Przeciwnie, obwód równoległoboku może być obliczony przez – dodanie podstawy i wysokości, i pomnożenie sumy przez 2.
Wniosek
Obie równoległoboki i romby są czworokątami, których boki są równoległe, przeciwległe kąty są równe, suma kątów wewnętrznych wynosi 360 stopni. Sam romb jest szczególnym rodzajem równoległoboku. Dlatego można powiedzieć, że każdy romb jest równoległobokiem, ale odwrotna sytuacja nie jest możliwa.
.