When and how should be used for handling missing data in randomised clinical trials – a practical guide with flowcharts

データを分析する準備ができたら、データの点検に基づいて、欠損データの処理に統計手法を使用すべきかを十分に評価する必要があります。 Bellらは、BMJ、JAMA、Lancet、New England Journal of Medicineに2013年7月から12月に掲載された無作為化臨床試験における欠損データの範囲と取り扱いを評価することを目的とした。 特定された77試験の95％が、何らかのアウトカムデータの欠落を報告していた。 一次解析で欠損データを処理するために最もよく使われた方法は、完全症例解析（45％）、シングルインピュテーション（27％）、モデルベースの方法（例えば、混合モデルや一般化推定方程式）（19％）、マルチインピュテーション（8％）であった .

Complete Case Analysis

完全症例解析とは、アウトカムデータを完備した参加者に基づく統計解析である。 データの欠損がある参加者は分析から除外されます。 冒頭で述べたように、欠損データがMCARの場合、完全症例解析はサンプルサイズが小さくなるため統計的検出力が低下しますが、観測されたデータに偏りはありません。 欠損データがMCARでない場合、完全症例解析による介入効果の推定値は根拠となる可能性があり、すなわち、有益性を過大評価し、有害性を過小評価するリスクがしばしば存在することになる。 完全症例解析が適用された場合の潜在的な妥当性については、「欠損データの処理に多重代入を用いるべきか」の項をご覧ください。

Single imputation

シングル代入を用いる場合、欠損値はある規則で定義された値で置き換えられます。 single imputationには、last observation carried forward（参加者の欠損値を参加者の最終観測値で置き換える）、worst observation carried forward（参加者の欠損値を参加者の最悪観測値で置き換える）、simple mean imputationなど、様々な形式が存在します。 単純平均置換では、欠損値はその変数の平均値で置換されます。 単一置換を使用すると，観測されていない各値が，既知の観測値と同じ重みを分析に与えるので，しばしば変動の過小評価になる． シングルインピュテーションの有効性は、データがMCARであるかどうかに依存しません。シングルインピュテーションはむしろ、例えば、欠損値が最後に観測された値と同一であるという特定の仮定に依存します。 これらの仮定はしばしば非現実的であり、single imputationはしばしば偏った方法であるため、十分に注意して使用する必要がある。

Multiple imputation

多重代入は無作為化臨床試験における欠損データを取り扱うための有効な一般法として示されており、この方法はほとんどの種類のデータで利用できる。 7349>

Multiple imputationを欠損データの処理に使用すべきか？

欠損データの処理にMultiple imputationを使用すべきでない理由

欠損データを無視することは有効か？

観測データの解析（完全症例解析）において欠損データを無視することは3つの状況下で有効であると考えられる。

1. a)

   欠損データの割合が約5%以下（経験則）であり、特定の患者群（例えば、非常に病気の人や非常に「元気な」参加者）が比較群のいずれかで特にフォローアップが失われることがありえない場合、完全ケース分析を主要分析として用いることができる 。 言い換えれば、欠損データの潜在的な影響が無視できるのであれば、解析において欠損データを無視することができる。 まず、一方のグループ（グループ1）でフォローアップを失った参加者全員が有益な結果を得た（例えば、重篤な有害事象がなかった）と仮定する「ベスト-ワーストケース」シナリオのデータセットを作成し、もう一方のグループ（グループ2）で結果が欠落した参加者全員が有害な結果を得た（例えば、重篤な有害事象があった）ことにします。 そして、グループ1でフォローアップを失った参加者全員が有害な結果を得ており、グループ2でフォローアップを失った参加者全員が有益な結果を得ていると仮定した「最悪のケース」のシナリオデータセットが作成される。 連続的な結果が使用される場合、「有益な結果」は、群平均に群平均の2標準偏差（または1標準偏差）を加えたものであり、「有害な結果」は群平均から2標準偏差（または1標準偏差）を引いたものであるかもしれない 。 2値化されたデータでは、これらのベスト・ワーストおよびワースト・ベストケースの感度分析は、欠損データによる不確実性の範囲を示し、この範囲が定性的に矛盾する結果をもたらさない場合、欠損データを無視することができます。 連続データの場合、2SDのインピュテーションは、（正規分布の場合）観測データの95％が与えられたときの不確実性の可能な範囲を表します

2. b)

   従属変数のみが欠損値を持ち、補助変数（回帰分析に含まれないが欠損値を持つ変数と相関があり、その欠損性に関連する変数）が識別されない場合、完全事例分析を一次分析として使用でき、欠損データを取り扱うために特定の方法を用いる必要はない。 例えばマルチプルインピュテーションを用いても追加的な情報は得られないが、マルチプルインピュテーションによってもたらされる不確実性により標準誤差が増加する可能性がある。

3. c)

   前述のように（欠損データの処理方法参照）、データがMCARであることが比較的確実である場合は、完全症例分析を行うだけでも有効である（「はじめに」参照）。 データがMCARであることが確実であることは比較的まれである。 MCARであるという仮説をLittleの検定で検証することは可能ですが、重要でないことが判明した検定を基にすることは賢明ではありません。 したがって、データがMCARであるかどうか合理的な疑いがある場合、たとえLittleの検定が重要でない（データがMCARであるという帰無仮説を棄却できない）場合でも、MCARを仮定すべきではありません。 欠損を処理するために多重代入や他の方法が使用されている場合、試験の結果が確定的であることを示すかもしれないが、欠損がかなりある場合はそうではない。 重要な変数で欠損データの割合が非常に大きい（例えば、40％以上）場合、試験結果は仮説を生成する結果としか見なされないかもしれません。 稀な例外は、欠損データの背後にある根本的なメカニズムがMCARとして記述できる場合です（上記の段落を参照）

   Do the MCAR and the MAR assumption both seems implusible? MNARデータを扱うために使用される方法の有効性は、観測されたデータに基づいて検証することができない特定の仮定を必要とします。 最良・最悪の感度解析は、理論上の不確実性の全範囲を示し、結論はこの不確実性の範囲に関連付けられなければならない。 7349>

   欠損値を持つ結果変数は連続的で、分析モデルは複雑（例えば、相互作用がある）か？

   この状況では、分析モデルと多重代入モデルの間のモデルの互換性の問題を避けるために直接最尤法の使用を考慮することができる（前者は後者よりも一般的である）。 一般的には直接最尤法を用いることができるが、我々の知る限り、市販の方法は現在のところ連続変数にしか利用できない。

   When and how to use multiple imputations

   上記の「欠損データの処理にmultiple imputationを用いてはならない理由」のいずれもが満たされない場合、multiple imputationが使用できる可能性がある。 過去数十年にわたり，欠損データを扱うためのさまざまな手順が文献で提案されてきた． 図1に、上記のような統計的手法による欠損データの取り扱いに関する考察の概略を示した（図1）。 1

   

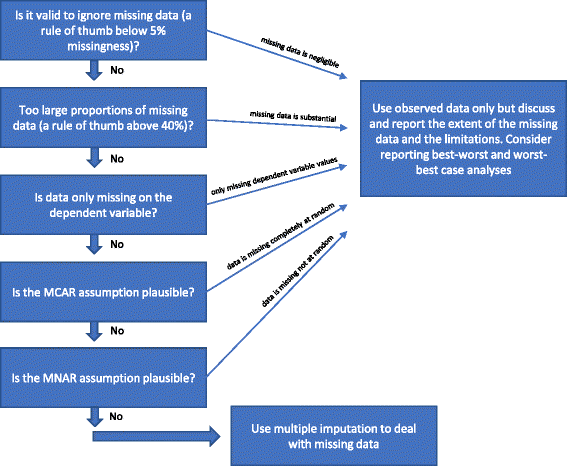
   フローチャート：無作為化臨床試験の結果を分析する際に、いつ欠損データを扱うために多重代入を用いるべきか

   多重代入は1970年代初頭に生まれ、長年にわたって人気を集めてきました。 多重代入は、欠損データを処理するためのシミュレーションに基づく統計的手法です。

   1. Imputation stepの3つのステップから構成される。 インピュテーション」は一般に、欠損データに対してもっともらしい値の1つのセットを表しますが、多重インピュテーションはもっともらしい値の複数のセットを表します。 multiple imputationを使用する場合、欠損値が特定され、plausible values imputationsのランダムなサンプル（complete datasets）で置き換えられます。 複数の補完されたデータセットが、選択されたインピュテーション・モデルによって生成されます。 理論的には5つのインピュテーションされたデータセットで十分であるとされてきたが，インピュテーションプロセスによるサンプリング変動を軽減するために，50データセット（またはそれ以上）が望ましいと思われる． 所望の分析は、インピュテーションステップ中に生成される各データセットについて別々に実行される。 これにより、例えば50個の解析結果が構築される。

   2. プーリングステップ。 各完了データの解析結果を1つのマルチプルインピュテーション結果に統合する。 50の解析結果はすべて同じ統計的重みを持っていると考えられるので、重み付けメタ解析を行う必要はない。

   インピュテーションモデルと解析モデルの間に互換性があるか、インピュテーションモデルが解析モデルよりも一般的であること（例えば、インピュテーションモデルは解析モデルよりも独立共変数を含むこと）が非常に重要である。 例えば，解析モデルが有意な交互作用を持っている場合，インピュテーションモデルもそれを含むべきである，解析モデルが変数の変換版を使用している場合，インピュテーションモデルも同じ変換を使用するべきである，などである． 1) 単値回帰分析，2) モノトニックインピュテーション，3) 連鎖式またはマルコフ連鎖モンテカルロ法（MCMC法）． 7349>

   単変量回帰分析では，従属変数と無作為化で使用される層別変数が含まれる． 層別化変数には、試験が多施設共同試験の場合は施設指標、通常は転帰と相関のある予後情報を持つ1つ以上の調整変数が含まれることが多い。 連続従属変数を使用する場合、従属変数のベースライン値も含まれるかもしれません。 統計手法を欠損データの処理に使用すべきでない理由」で述べたように、従属変数のみが欠損値を持ち、補助変数が識別されない場合、完全な症例分析を行うべきで、欠損データを処理するために特別な手法を使用すべきではありません。 補助変数が同定された場合、単一変数のインピュテーションが実行されるかもしれない。 連続変数のベースライン変数に有意な欠損がある場合、完全症例解析は偏った結果を提供する可能性があります。 したがって，すべてのイベントで，ベースライン変数のみが欠損している場合，単一変数インピュテーション（必要に応じて補助変数を含むか含まない）が行われる

   従属変数とベースライン変数の両方が欠損していて，欠損が単調である場合，単調インピュテーションが実行される． 患者が行で、変数が列で表現されるデータ行列を仮定する。 このようなデータ行列のmissingnessは，任意の患者について， (a) 値が欠損している場合，その位置の右側のすべての値も欠損しており， (b) 値が観察されている場合，この値の左側のすべての値も観察されているように，その列を並べ替えることができる場合，単調であるといわれる． 欠損が単調であれば、複数の変数が欠損値を持つ場合でも、多重代入の方法は比較的簡単である . この場合，欠損値が一度に各変数についてインプットされる逐次回帰インピュテーションを使用して，欠損データをインプットすることは比較的簡単である． 多くの統計パッケージ（例えば，STATA）は，欠測が単調かどうかを分析することができる

   欠測が単調でない場合，連鎖方程式またはMCMC法を用いて多重代入が行われる． 補助変数は利用可能であればモデルに含まれる。 図2

   

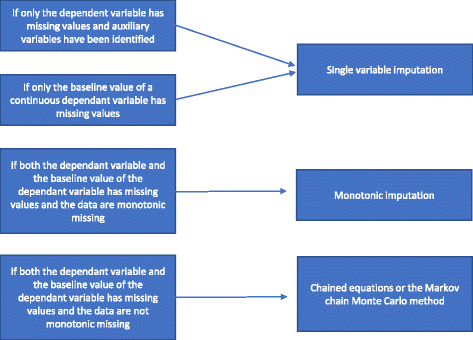
   多重代入のフローチャート

   Full information maximum likelihood

   Full information maximum likelihoodは欠損データに対する代替法であり、欠損データを処理するのに最も適した手法の一つである。 最尤推定の原理は、結果（Y）と共変量（X1,…, Xk）の共同分布のパラメータを推定することで、それが真であれば、実際に観察された値を観察する確率を最大化することにある。 ある患者で値が欠損している場合、欠損データのメカニズムが無視できるのであれば、欠損データのすべての可能な値について通常の尤度を合計することによって尤度を得ることができます。 この方法は完全情報最尤法と呼ばれる．

   完全情報最尤法は多重代入と比較して長所と短所がある。

   多重代入と比較した完全情報最尤法の長所

   1. 1)

      実施がよりシンプルである。

   2. 2)

      Multiple imputationと異なり、full information maximum likelihoodは、imputationモデルと分析モデルの間の非互換性の問題がない（「Multiple imputation」参照のこと）。 多重代入の結果の妥当性は、代入モデルと解析モデルの間に非互換性がある場合、あるいは代入モデルが解析モデルよりも一般的でない場合に疑問視されることになる。）

      多重代入を使用する場合、生成された各データセット（代入ステップ）のすべての欠損値は、もっともらしい値のランダムなサンプルで置き換えられます。 したがって、’a random seed’が指定されない限り、multiple imputation分析を実行するたびに異なる結果が表示されます。 同じデータセットで完全情報最尤法を使用した場合の解析は、解析が実行されるたびに同じ結果が得られ、したがって結果は乱数種に依存しません。

   Limitations of full information maximum likelihood compared to multiple imputation

   full information maximum likelihoodの限界は、多重代入と比較して、特別なソフトウェアを使用しないと使用することができない点である。 設計された予備的なソフトウェアは開発されているが、そのほとんどは市販の統計ソフト（例えば、STATA、SAS、SPSS）の機能を欠いている。 STATA（SEMコマンドを使用）およびSAS（PROC CALISコマンドを使用）では、連続従属（結果）変数を使用するときのみ完全情報最尤法を使用することが可能である。 ロジスティック回帰とCox回帰では、欠損データに対する完全情報最尤法を提供する唯一の商用パッケージはMplusである

   完全情報最尤法を使用する際のさらなる潜在的制限は、多変量正規性の仮定があることです。 それにもかかわらず、多変量正規性の仮定に違反することはそれほど重要ではないかもしれないので、分析にバイナリ独立変数を含めることが許容されるかもしれない。 表1および表2は、出力と、欠損データを処理する異なる方法が異なる結果を生成する方法を示しています。

   パネル値回帰分析

   パネルデータは通常、最初の行が変数名を含み、その後の行（各患者に1つ）が対応する値を含むいわゆるワイドデータファイルである。 転帰は、転帰の計画的、時間的測定ごとに1つずつ、異なる変数で表現されます。 データを分析するために、ファイルを、アウトカム値、測定時間、およびアウトカム変数のものを除く他のすべての変数値のコピーを含む、計画されたアウトカム測定ごとに1レコードのいわゆるロングファイルに変換する必要があります。 時間指定されたアウトカム測定値間の患者内相関を保持するために、一般的には、データファイルのワイド形式での多重入力と、ロング形式に変換された後の結果ファイルの分析を実行する。 連続アウトカム値の分析には proc mixed (SAS 9.4) を、その他のタイプのアウトカムには proc.glimmix (SAS 9.4) を使用することができます。 これらの手順は、結果データに直接最尤法を適用するが、共変量値が欠損しているケースは無視するので、従属変数の値のみが欠損しており、良い補助変数がない場合、この手順を直接使用することができる。 そうでない場合は，多重入力の後，proc.mixed またはproc.glimmix（どちらか適切な方）を使用する必要がある． 7349>

   感度分析

   感度分析は、一次分析と比較して異なる方法でデータを処理する一連の分析として定義されることがある。 感度分析では、一次分析で行われたものとは異なる仮定が、得られた結果にどのように影響するかを示すことができる。 感度分析は、事前に定義され、統計解析計画に記述されるべきであるが、追加のポストホック感度分析が正当化され、有効であるかもしれない。 欠損値の影響が不明確な場合は、以下の感度分析を推奨する：

   1. 我々はすでに、欠損データによる不確実性の範囲を示すために、ベスト-ワーストおよびワースト-ベストケース感度分析の使用を説明している（「欠損データを扱うために方法を使用すべきかどうかについての評価」参照）。 最良-最悪および最悪-最良の場合の感度分析に関する前回の説明は、二項従属変数または連続従属変数のいずれかにデータがない場合に関連していましたが、これらの感度分析は、層別変数、ベースライン値などにデータがない場合にも使用することができるかもしれません。 欠損データの潜在的な影響は、各変数について個別に評価されるべきで、すなわち、欠損データを持つ各変数（従属変数、結果指標、層別変数）について、最良-最悪ケースと最悪-最高ケースのシナリオが一つずつあるべきである

   2. 例えば、多重インピュテーションが用いられるべきと決定した場合、これらの結果は与えられた結果の主要結果となるはずである。 各一次回帰分析には、必ず対応する観察された（または利用可能な）症例分析が補足されるべきである。

   混合効果法が用いられる場合

   多施設の試験デザインを使用することは、妥当な時間枠内で十分な数の試験参加者を募集することがしばしば必要となる。 また、多施設共同試験のデザインは、その後の知見の一般化のためのより良い基盤となる。 無作為化臨床試験で最もよく使われる解析方法は、少数の施設でうまく機能することが示されている（二値の従属的な結果を解析する場合）。 比較的大きな施設数（50施設以上）では、「施設」をランダム効果として使用し、混合効果分析法を使用することが最適であることが多い。 また、縦断的なデータを分析する場合にも、混合効果分析法を使用することが有効であることが多いでしょう。 状況によっては、インピュテーションのステップで「ランダム効果」共変量（例えば「中心」）を固定効果共変量として含み、分析のステップで混合モデル分析または一般化推定方程式（GEE）を使用することが有効である場合もあります。 しかし，混合効果モデル（例えば，’center’をランダム効果として）の適用は，多重代入をモデル化するときに，データの多層構造を考慮に入れなければならないことを意味する． 現在、これを行うための商用ソフトは直接利用できません。 しかし、STATAとインターフェイスできるREALCOME パッケージを使用することができます。 このインターフェースは、STATAからREALCOMに欠損値を含むデータをエクスポートし、そこで、データのマルチレベルの性質を考慮に入れ、連続変数を含むMCMC法を用いて、潜在正規モデルを使用することにより、離散データを適切に取り扱うことができるようなインピュテーションが行われます。 インピュテーションされたデータセットは，STATAの ‘mi estimate:’ コマンドを使用して分析することができ，これは，STATAの ‘mixed’ 文（連続結果の場合）または ‘meqrlogit’ 文（バイナリまたは序数結果の場合）と組み合わせて使用することができる． しかし、パネル・データの分析では、例えば、同じ患者内の測定値（レベル1）、センター内の患者（レベル2）、センター（レベル3）など、データが3つ以上のレベルを含む状況に簡単に直面することがあります。 収束しなかったり、標準誤差が不安定になったりするような複雑なモデルで、市販のソフトウェアを使用できない場合は、中心効果を固定として扱うか（直接、または統計解析計画に規定されている手順を用いて、小規模中心を一つまたは複数の適切な規模の中心へ合併する）、中心を共変量として除外することをお勧めします。 無作為化が施設ごとに層別化されている場合、後者のアプローチは標準誤差の上方バイアスにつながり、その結果、やや保守的な検定手順となる。