Lotka-Volterra Equation

The Lotka-Volterra equations describe an ecological predator-prey (or parasite-host) model that assumes that you are that, 固定された正の定数（獲物の成長率）、（捕食者が獲物を破壊する率）、（捕食者の死亡率）、（捕食者が獲物を消費して増加する率）の集合に対して、以下の条件が成立している。

1. 獲物集団は（獲物の数に比例）の割合で増加するが、同時に（獲物の数と捕食者の数の積に比例）の割合で捕食者によって破壊される。

2.捕食者集団は速度（捕食者の数に比例）で減少するが、速度（やはり餌の数と捕食者の数の積に比例）で増加する。

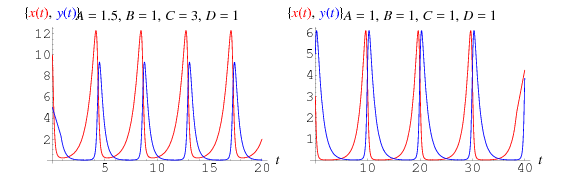
これによって連立微分方程式

が得られる。

			(1)
			(2)

上にプロットした解答を示す。 獲物は赤で、捕食者は青で示した。 このようなモデルでは、獲物の曲線は常に捕食者の曲線をリードしています。

臨界点が発生するのはのときです。 だから

			(3)
			(4)

したがって、唯一の静止点はに位置することになる。