What’s the difference between concave and convex?
凹と凸の違いを最も一般的に表現するならば、中空でボウル状のものは凹、ラグビーボールやサッカーボールに似たものは凸型と言えるかもしれません。 しかし、凸と凹がよく誤用される理由は、おそらくこの2つの言葉が私たちが望むほど単純ではないからでしょう。
ほとんどの文法資料は、凸と凹を解読するために、いかにニーモニックを使うことが可能であるかを、単語の洞察を通して主張しています。 凹を何かが「陥没する」という出来事と関連付ける考え方は、表面の特徴について学ぶのに役立ちますが、この考え方をグラフを含む主題に関連付けるのは混乱を招きます。 凹や凸のような言葉をどの文脈で使うか決めたら、その技術的な側面を学ぶことで、日常会話で自信を持って使うことができるようになるのです。

凹の意味は?
凹は形容詞または名詞として、物体や表面が内側に曲がっていたり、お椀のようにくぼんでいる形状を表すために使用されます。 凹の文例としては、
“She scooped the ice cream from the container, leaving a concave footprint.”
The Oxford Dictionary of Word Histories によると、凹という言葉は中世後期の英語に由来しています。 Concave と concavity はラテン語の concavus (con- and cavus) を表し、これは「一緒に」「空洞」と訳される (“Concave,” 110)。
凹の同義語は以下の通り。
凹む、落ち込む、くぼむ、くぼむ、凹む、沈む。
凹の反意語は以下の通り。
膨らむ、凸凹、突出する、隆起する。
凸の意味とは?
凸(コンベックス)とは、丸みを帯びた、または湾曲した物体や面を表す形容詞です。 物体に関して、凸の物体の中央の表面は、その外側の角よりも広くなっています。 文中の凸の例としては、
“I fell into poison ivy and now have red, convex bumps all over my skin. “などがあります。
凸の類義語は以下の通りです。
弧を描く、曲がる、膨らむ、盛り上がる。
凸の反意語は以下の通りです。
凹んでいる、沈んでいる。
凹型関数と凸型関数
凸型関数は、領域の中点または中央の整数が区間の平均を超えないグラフ上の連続線を表します。 凹関数は凸関数と正反対で、f(x)が凹であるためには、f(x)は負でなければならないからである。 5822>
上に凹む=凸=下に凸
下に凹む=凹=上に凸
凹と凸の違いは、グラフにするとより明確になります。 凸の関数は上に開き、凹の関数は下に開いていることに注目してください。
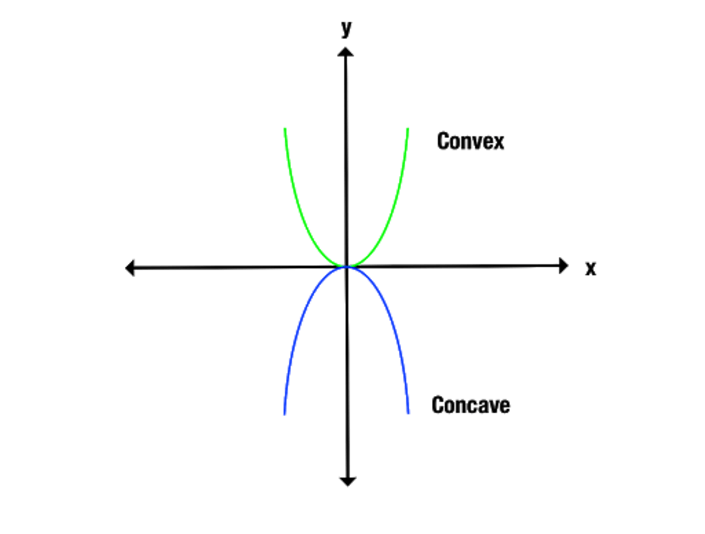
凹と凸の関数を識別するもう一つの方法は、グラフ上の点をx軸に沿って結ぶことです。 凹型の関数はグラフの下にある線だけを結び、凸型の関数はグラフの上にある線だけを出します。
さらに微積分を使えば、関数が凸か凹かを読み解くことができる。 f(x)の2次導関数が0より大きければ、その関数は凸である。 しかし、f(x)の2次導関数が0より小さければ、その関数は凹である。
凸多角形と凹多角形
慌てないでください、凸と凹という言葉は幾何学にも使われるんですよ。 凸型と凹型は、多角形(最低3つの辺と角度を持つ図形)を基準に語られることが多いようです。
正多角形は辺と角が等しいものが存在しますが、凸と凹の多角形はもう少し複雑です。 凸多角形は180度より小さい内角を含み、凹多角形は180度より大きい内角を1つ以上含む。
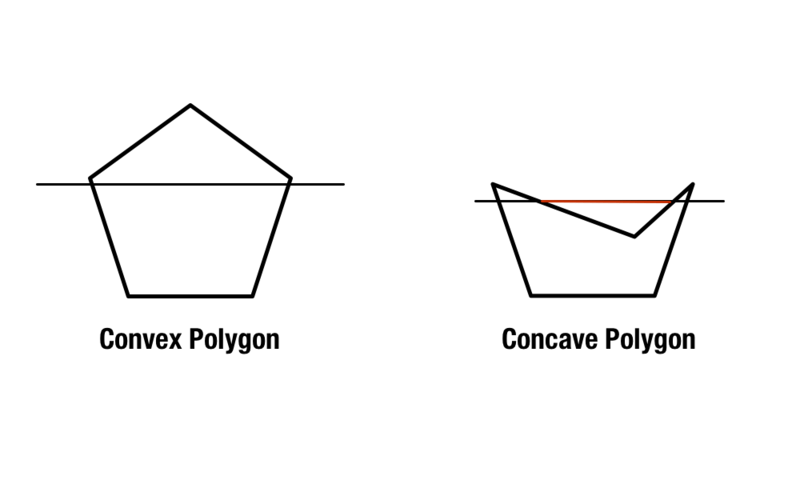
凹凸多角形を識別する第二の方法は、図形の角から対角線を二本引くことである。 すべての線が形状の中に存在する場合、その形状は凸である。 形状の外側を横切る線が少なくとも1本あれば、それは凹形状である。
凹面鏡と凸面鏡
凹面と凸面という言葉は、鏡やレンズなどの光学物について議論するときによく使われます。 凸面は泡のように外側に突出し、幅が広く見える効果があります。 凸面鏡は、ドライバーがコーナーや潜在的な死角の周りの広い視野を必要とする駐車場内で一般的に見られます。

対照的に、凹面鏡は内側に湾曲しており、逆さまに拡大された反射を生成します。 サウス ウェールズ大学物理学部が示したように、光沢のあるスプーンを持っている人は、スプーンに映った自分の姿を見ることで、この観察結果を試すことができます。 食べ物をつまむスプーンの凹面では、自分の反射が細長く歪み、逆さまに見えるようになります。 しかし、スプーンを凸面に反転させると、あなたの姿は直立し、小さく映ります。
凸面と凹面で反射が大きく異なるのは、表面が外側に曲がっていても内側に曲がっていても、鏡自体が球体の一部であるためです。 球体の表面は平らではないので、その表面で反射した光は鏡に接触するまでに異なる距離を移動することになります。
表面のどの部分に光が当たるかによって、光線は近くの表面で反射して、より焦点の合った部分が見えるようになります。 このため、スプーンの内側を見ているとき、スプーンの表面に最も近い部分の反射しか見えないことがあります–たとえそれがまだ小さく見えるとしても。 また、スプーンの中に指を入れると、鏡の表面は同時に2つ、3つの異なる反射をすることがあります。
凹レンズと凸レンズ
眼鏡、コンタクト、双眼鏡、望遠鏡など、日常的なものには凹レンズと凸レンズが存在します。 凸面鏡や凹面鏡での光の反射の科学と同様に、光が凹レンズや凸レンズを通過して可視像を生成する方法にもパターンがあるのです。

凸レンズ
Manocha Academyによると、凸レンズは縮小、拡大、内向の画像を作ることができるため、収束レンズと呼ばれています。 凸レンズを通してどれだけ正確に像が見えるかは、レンズの焦点に対象物がどれだけ近いかによって決まります。 どんな凸レンズでも、レンズの両側には対称的な焦点位置が存在します。
凸レンズを通してどのように正確にオブジェクトが生成されるかは、3つの原則で予測される:
原則1:凸レンズを通過する光線は、球面レンズの絶対中心を通る中心線である主軸と平行である。 光がレンズに接触すると、光は屈折して反対側の焦点位置を通過する。
原理2:凸レンズの中心を通過した光線は、反対側で直線的に進む。
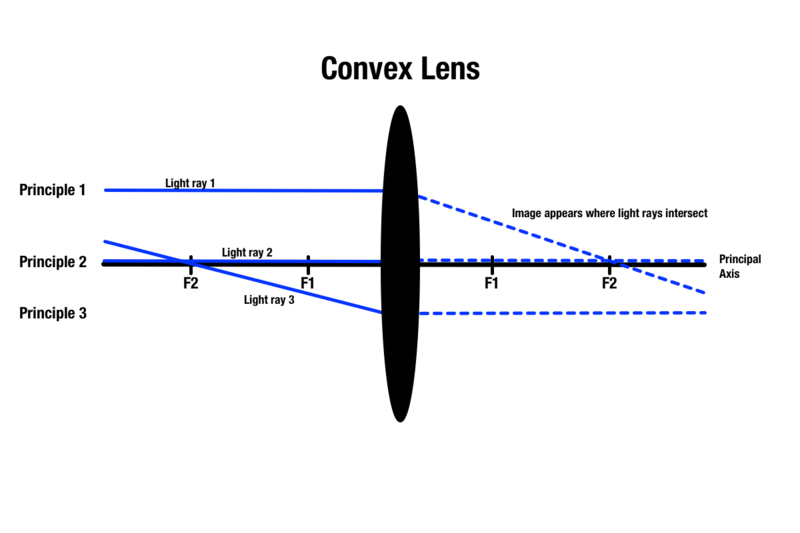
凸レンズによる画質を予測するための3つの原則がありますが、光線図を描きながらオブジェクトに適用できるのは2つの原則のみです。 任意の2つのプリンシパルは、レンズの反対側で光の交点を生成し、それが物体の像が現れる領域を示すことになります。
凸レンズに物体が遠くなるほど、反対側の像は小さくなり、凸レンズに物体が近くなるほど、像は大きく見える。 最も近い焦点位置を過ぎたところにある物体は、その後ろに大きな像ができる。
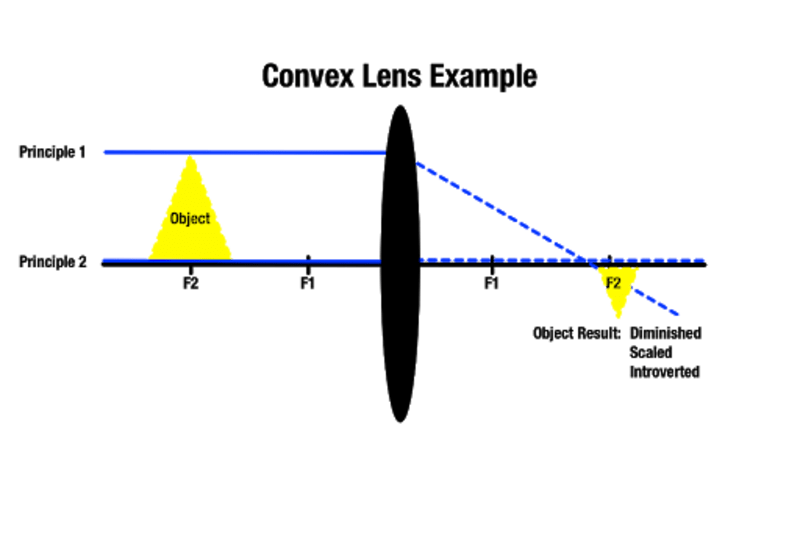
どの焦点に物体を置くかによって、おおよその大きさの画像を作ることができるのである。 また、通過する光線が向こう側で平行になり、決して交わることがなければ、目に見えない実像を作り出すことも可能です。 この場合、生成される画像は無限に離れたところに存在することになります。
凹レンズ
凹レンズは内側に湾曲しているので、直径が太く、中心部が細くなります。 凹レンズの形状は、レンズと接触した光が広がるため、仮想の物体を小さく見せることができます。 凹レンズによる光の広がりは、懐中電灯のように中央の光源を広い面積で使用できる道具に最適なレンズといえます。
凹レンズは、凸レンズと同じように3つの原理で像を結びます。
原理1: 物体の上方で主軸に平行に進む光線は、レンズとの接触で屈折し、最も近い焦点の方向から来るように見える。
原理2:凹レンズの中心を通過する光線は、屈折せずに通過する。
原理3:凹レンズの反対側の焦点に向けられた光線は、屈折して主軸に平行になる。
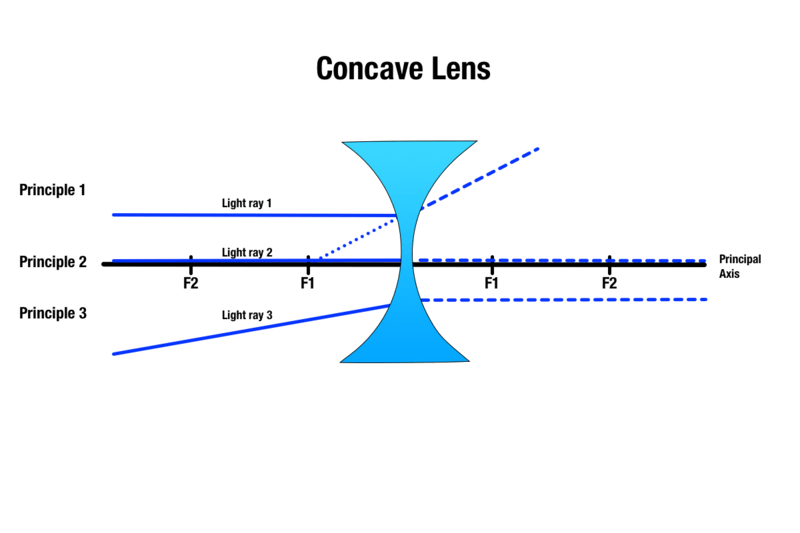
凹レンズからの物体の距離によって、物体像の大きさは変わるが、作られる像は常に仮想で直立して小さく、レンズの物体側と同じ側に見える。
Concave vs. convex in writing
凹と凸という言葉は互いに逆で、基本的には次のような言葉を対比するのと同じように、物体や表面の形状を表現します:
- Small vs. Caps. big
- Tall vs. short
- Slim vs. wide
- Round vs. flat
凹凸は専門用語なので、散文に記述的に使用すると、カジュアルオーディエンスにはより隠喩的または抽象的な解釈が生まれる可能性があります。 このことが意味するのは、作家が凹や凸をその典型的な使用の範囲外で使うことにした場合、作家は自分の文章をどれだけ明確にするつもりなのかを決めなければならないということです。
形容詞を考える
文学で凹や凸を使う顕著な例として、アメリカの作家デヴィッド・フォスター・ウォレス(略してDFW)の文章を考えてみましょう。 DFW は、その複雑で技術的な文体で有名ですが、そう、彼は何度か名詞を表すのに convex と concave を使いました。 ウォレスは以下の例で凹と凸を使っています:
“私の手眼はまあまあだったが、私は大きくも素早くもなく、凹に近い胸と親指と小指でブレスレットができるほど細い手首を持っていた…”.
– “テニス、三角法、トルネード。 中西部の少年時代」『ハーパーズ・マガジン』。
– “ノーザンプトンの秩序と流動”、「コンジャンクション」、心綱の引きで開く人形の目。
DFWの例を使うことのポイントは、単に作家が数学的な文脈以外でどのようにconvexやconcaveを使っているかを示すことではなく、作家が専門用語や抽象用語を使うことが読者に明確に伝えるために有用かどうかを検討することにあります。
最初のDFWの例では、彼は何かの構造を記述しているので、凹の使用は理にかなっています。 しかし、感情や思考などの非目的名詞を表現するために凹や凸を使用すると、説明しようとしていることの意味がわからなくなる傾向があるのです。 2 番目の DFW の例では、convex と concave の使用は文字通りと比喩の両方であるため、微妙な境界線を歩くことになります。 関連用語
関数とは何か
関数とは、グラフ上の直線の方程式を指します。 関数はグラフ上の線ごとに異なりますが、一般的には
f(x) = x + 1
任意の線関数で、従属変数は通常 f(x) であり、関数内の任意の未知の変数を独立変数と呼びます。
ドメインとは何ですか。
ドメインとは、直線の関数に対応するグラフ上の独立変数の集合のことです。 ドメインは、方程式の任意の実出力に対応するグラフ上の特定の点を位置づけるので、理解することが重要です。
範囲とは何ですか。
関数の範囲は、従属変数の有効値を生成するグラフ上のx軸またはy軸に沿って任意の可能な値を表します。 すべての最小および最大整数は、x軸またはy軸に変数を代入することによって識別されます。
区間とは何ですか?
区間とは、直線の整数を表す数の集合で、ドメインと呼ばれるものである。 閉区間は直線の2つの有限点を含み、整数の範囲外ではもはや直線が存在しない。 開区間とは、直線の領域の絶対的な終端を表さない整数の集合のことです。
Test Yourself!
次の多肢選択問題で凸と凹の違いをどれだけ理解しているかを確認します:
- 光るスプーンを眺めているとき、自分の姿が逆さまになっていることに気付きます。 スプーンの表面は_________面である。
a. 凸面
b. 鏡
c. 凹面
d. 金属 - 関数のグラフ化では、凸型関数をこう呼ぶことがある。
a. 上に凹む
b. 下向きに凸
c. 下に凸
d. AとB - 次のうち、凹面を表現していないものはどれでしょう。
a. 中空の半球体
b. 目のレンズ
c. シリアルボウル
d. 半球体 - 次のうち、凸面を表現していないものはどれでしょう。
a. ファミリーガイのキャラクター、スチュウイ
b. 球体
c. 駐車場の鏡
d. サッカーボール - 次のうち、凹の多角形として存在できない形はどれでしょう。
a. ペンタゴン
b. 六角形
c. 三角形
d. 八角形
答え
- C: 凹
- D: AとB
- D: 半球
- B: 球
- C: 三角
資料:
- Bourne, M. “Domain and Range of a Function.”. Interactive Mathematics, Jan.4, 2019.
- “Concave”(凹). メリアム・ウェブスター辞典, 2019.
- “凹”. オックスフォード・ワードヒストリー辞典』Ed. Chantrell, 2002, p. 110.
- “Concave and Convex Mirrors”(凹面鏡と凸面鏡). まのっちアカデミー、YouTube、2019年。
- “凹レンズ: 定義&用途.”. 勉強ドットコム、2019年
- “凸”. メリアム-ウェブスター辞典、2019年。
- “凸レンズと凹レンズ”. マノカアカデミー、YouTube、2019年。
- “数学/多角形を理解する”. 株式会社ラーンハイブ、2018.
- “Reflection from a concave mirror.” UNSW Physics, YouTube, 2017.
- Wallace, D.F. “Tennis, Trigonometry, Tornadoes. “テニス、三角法、竜巻。 中西部の少年時代” ハーパーズ・マガジン、1991年
- Wallace, D.F. “Order and Flux in Northampton.”(ノーザンプトンにおける秩序と流動)。 Conjunctions, 1991.
- Weisstein, Eric W. “凹型関数.”. MathWorld-A Wolfram Web Resource, n.d.
- Weisstein, Eric W. “Convex Function.” (凸関数). MathWorld-A Wolfram Web Resource, n.d.
Word Counterは、単語、文字、文、パラグラフ、ページをリアルタイムでカウントし、スペルや文法をチェックするための動的なオンラインツールです。