はじめに
このページでは、オイラー解析で質量の保存を強制する連続方程式について説明します。 これは厳密には材料の挙動を記述するものではないが、結果として得られる方程式は材料の挙動を記述する構成モデルを代数的に操作するための恒等式としてよく使われる。 そのため、復習しておくとよいだろう。
Conservation of Mass
連続の式は、非核連続体力学の解析において質量が保存されることを反映したものである。 この式は、制御体積に流入・流出する質量を加算し、正味の流入量をその中の質量の変化率に等しくすることによって展開される。 これは、以下の図に示されています。
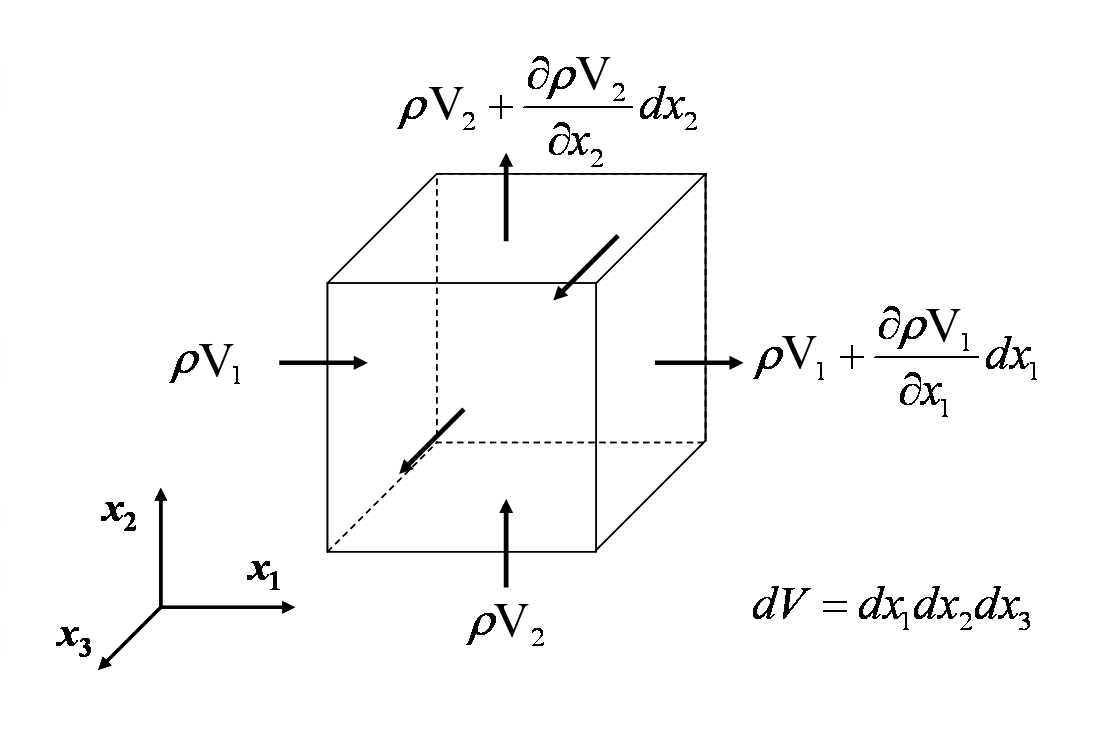
差動制御体積に流入・流出するすべての質量流量を等化すると
Cancelling terms and dividing through by ୧(dx_1 dx_2 dx_3 ა) は
となり、並べ替えると
となる。これを簡潔に書くと

重要ポイント
以上が最終形となります。 質量保存を強制する連続方程式の完全な、そして最も一般的な形です。 これは流体だけでなく、すべての材料に適用されます。 つまり、固体にも適用される。 これは単一のスカラー方程式であり、gradienttermsが(next({Partial}over)were \partial x_i}) なのでEulerian in natureであることに注意。
これのEulerian formに対応するLagrangianがあるかと思うかもしれません。 ある。 通常、次のように書かれる。これは、変形した状態での質量の微分チャンクが、変形していない状態での元の値( \rho_o dV_o) と等しくなければならないという単純なものである。 この場合、時間に関する微分はゼロとなり、
2番目の特殊ケースは非圧縮性の場合である。 \この場合、時間に関する微分はゼロになり、needing only
Thailand
The result is simple enough that is often expanded out of the equation.

Material Derivative
以下は密度ベクトルと速度ベクトルを分離するためのもので、特筆すべきことである。 まず、連続方程式の発散項に積の法則を適用します。
そして、That({Partial \rho }+{Partial v} \cdot \nabla \rho}) is just the material derivative of the density, \({D \rho \over D t}) に注目しましょう。
だから連続の式は
\
もし材料が非圧縮性であれば, \(\rho) cannot change, so\( {D \rho \over D t} \) must be zero.と書くことができる, leaving
And then divide through by \(rho\) (because it’s not zero) to get

Continuity Equation Example
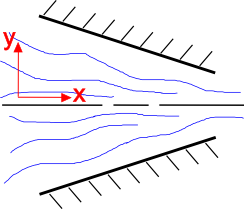
右図のように断面積が減少すると流体が速くなることは直観的に分かると思います。 これを説明するのが連続の式である。 非圧縮性流体の2次元定常流れ場を考える。このときの連続の式は
流れのy成分(v_2)を見ることから始めよ。 The geometry ofthe converging nozzle force the \(v_2) component to flow upward whenặc (y \lt 0ờg), and flow downward when \(y \gt 0ờg). だから、”So \(v_2) when 椎名(y) \lt 0″、”So \(v_2) when 椎名(y) 0 “なんだ。
The net effect of this is that \({ {partial v_2 \over \partial x_2} \lt 0)in the converging nozzle.は、収束するノズルの中にある。
しかし、連続の方程式は、2つの偏微分の和が0に等しくなければならないと定めています。 つまり、2つ目の偏微分が0より小さければ、
となり、このことは流体が加速していることを意味する
。