大きな数字を素早く掛ける方法

ここでは、大きな数を高速で乗算するために線形代数と組み合わせた分割統治アルゴリズムの巧妙なアプリケーションを学ぶことができます。 また、Big-O記法についても紹介します！

実際、この結果はあまりにも直感に反しているため、偉大な数学者コルモゴロフは、これほど高速なアルゴリズムは存在しないと推測しています。 (そしてBig-O記法の紹介)

私たちは皆、学校で掛け算を習ったことを覚えています。 実は、私にも告白があります。 ここは判断のつかない場所であることをお忘れなく 😉

学校では、運動場で遊ぶには強すぎる雨が降っているときに「ぬれぎぬ」をしたものです。 他の（普通の、楽しいことが大好きな、肯定的な形容詞の）子供たちがゲームをしてふざけている間、私は時々紙をもらって、ただひたすら大きな数を掛け合わせたものです。 計算の楽しさ スーパー144」という掛け算の競技もあって、スクランブルされた12×12のマス目（1～12まで）をできるだけ早く掛け合わせなければならなかったんです。 私はこの練習を欠かさず、あらかじめ用意した練習用紙をコピーして、ローテーションで使っていたほどです。 最終的には2分1秒まで短縮しましたが、その時点で走り書きの限界に達していました。

このように掛け算に夢中になっていましたが、もっとうまくできるはずだという思いはありませんでした。 掛け算にこれだけの時間を費やしたのに、アルゴリズムを改善しようとしなかったのです。

103と222の掛け算を考えてみましょう。

2回3回1+2回0回10+2回1回100+20回3回1+20回0回10+20回1回100=22800を計算します

一般に、n桁の数に掛けるにはO（n2）演算が必要です。 big-O」表記は、演算回数をnの関数としてグラフ化する場合、n²の項が本当に重要であることを意味しています。 9197>

今日、私たちは子供の頃の夢をすべて叶え、このアルゴリズムを改良します。 しかし、その前に!

Big-O

下の2つのグラフを見てください

数学者に「x² と x²+x^(1/3) は同じですか」と尋ねると、おそらく彼らはコーヒー カップに吐いて泣き出し、位相について何かつぶやくことでしょう。 少なくとも、（最初は）私の反応はそうでしたし、私はトポロジーについてほとんど何も知りません。 それらは同じではありません。 しかし、私たちのコンピュータはトポロジーを気にしていません。 コンピュータは、私がコンピュータについて何も知らないので、説明できないほど多くの点で性能が異なります。

しかし、スチームローラーをファインチューニングする意味はありません。 もし 2 つの関数が、その入力の大きな値に対して、同じ大きさのオーダーで成長するなら、実用的な目的のために、それは関連する情報のほとんどを含んでいます。

上のグラフで、2 つの関数が大きな入力に対してかなり似ていることがわかります。 しかし同様に、x² と 2x² も似ています。後者は前者の 2 倍だけ大きいのです。 x=100では、一方は10,000、一方は20,000です。 つまり、一方が計算できれば、もう一方もおそらく計算できる。 一方、指数関数的に成長する関数、例えば10^xは、x = 100の時点ですでに宇宙の原子数をはるかに超えている。 (10¹⁰⁰ >>> 10⁸⁰ これは私のググったところによると、宇宙の原子の数に関する推定値、エディントン数です*)

*実は DuckDuckGo を使いました。

多項式として整数を書くことはとても自然ですがとても非自然でもあります。 1342 = 1000 + 300 + 40 + 2 と書くことは非常に自然です。 1342 = x³+3x²+4x + 2 (x = 10) と書くのは少し変です。

一般に、b 基数で書かれた、一桁が n の大きな二つの数を掛け合わせるとします。 n桁の数をそれぞれ多項式で書く。 n桁の数をr個に分割すると、この多項式はn/r個の項を持つ。

例えば、b=10、r=3とすると、我々の数は142,122,912

これを

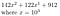
r=3、10進法で書いた我々の数は9桁だったのでこれは非常にうまくいきました。 rがnを完全に割り切れない場合は、先頭に0をいくつかつければよいのです。 9197>

27134 = 27134 + 0*10⁵ = 027134、これを

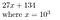
なぜこれが役に立つかというと、それは……………。 多項式Pの係数を求めるには、多項式が次数Nであれば、N+1点でサンプリングすれば係数を求めることができます。

例えば、次数5の多項式x⁵＋3x³ ＋4x-2を6点でサンプリングすると、多項式全体が求まります。

直感的には、次数5の多項式は、1、x、x2、x³、x⁴、x⁵の6つの係数があると考えられます。 6つの値と6つの未知数があれば、その値を求めることができます。

（線形代数を知っていれば、xの異なる累乗を線形独立ベクトルとして扱い、情報を表す行列を作り、行列を反転すれば、出来上がり）

Sampling polynomials to determine coefficients (Optional)

ここで、多項式をサンプリングしてその係数を推理する論理についてもう少し深く見てみましょう。

ここで示すのは、次数Nの2つの多項式がN+1点で一致するならば、それらは同じでなければならないということです。 つまり、N+1点は次数Nの多項式を一意に特定する。

次数2の多項式を考えてみよう。 これはP(z) = az² +bz + cの形です。代数学の基本定理により、この多項式は因数分解することが可能です（恥ずかしながら、私はこの証明を数ヶ月かけてまとめ、ここに書き上げました。 つまり、A(z-r)(z-w)

z = r と z = w で、多項式は 0 に評価されることに注意してください。 仮にw,r,sと呼ぶ3つの根があったとする。そしてこの多項式を因数分解する。 P(z) = A(z-r)(z-w) となる。 次に、P(s) = A(s-r)(s-w) となる。 0でない数をかけると0でない数になるから、これは0にはならない。 これは、当初の仮定がsが多項式Pの根であったため、矛盾している。

この議論は、基本的に同じ方法で次数Nの多項式に適用できる。

さて、次数Nの二つの多項式PとQがN+1点で一致したとする。 すると、それらが異なる場合、P-QはN+1点で0となる次数Nの多項式となる。 先に述べたように、次数Nの多項式は最大でN個の根を持つので、これは不可能である。 したがって、我々の仮定は間違っていたことになり、PとQがN+1点で一致すれば、それらは同じ多項式となります。

Seeing is believing: n/r = 24/4 = 6

p = 292,103,243,859,143,157,364,152 となります。

そしてそれを表す多項式をPとします。

P(x) = 292,103 x³ + 243,859 x² +143,157 x+ 364,152

でP（10⁶） = pです。

この多項式は3次なので4箇所サンプリングすれば全ての係数が求まるわけですが、その係数の計算を行うには、P(x)とP(x)が必要です。 9197>

• P(0) = 364,152
• P(1) = 1,043,271
• P(-1) = 172,751
• P(2) = 3,962,726

特徴はすべて6桁または7桁であることです。 これはもともとpにある24桁と比較してのことです。

pにqを掛けてみましょう。q = 124,153,913,241,143,634,899,130 とすると

Q(x) = 124,153 x³ + 913,241 x²+143,634 x + 899,130

t=pqを計算すると恐ろしいかもしれませんね。 Pは次数r-1=3の多項式、Qは次数r-1=3の多項式ですから、Tは次数2r-2=6の多項式となります。

T(10⁶) = t = pq

T(10⁶) = P(10⁶)Q(10⁶)

コツは、pとqを直接掛け合わせるのではなく、Tの係数を計算する点です。 そうすると、T(1⁰⁶)の計算は簡単で、1⁰⁶をかけるには後ろに0を6個つければいいだけだからです。 足し算はコンピュータにとって非常にコストのかからない動作なので、すべての部分を合計するのも簡単です。

Tの係数を計算するには、6次の多項式なので、2r-1=7点でサンプリングする必要があります。 おそらく小さい整数を選びたいので、

• T(0)=P(0)Q(0)=364,152*899,130
• T(1)=P(1)Q(1)=1,043,271*2,080,158
• T(2)=P(2)Q(2)=3,962,726*5,832 とします。586
• T(-1)=P(-1)Q(-1)= 172751*1544584
• T(-2)=P(-2)Q(-2)= -1,283,550*3,271.0
• T(-1)=P(-1)Q(-2)=1,283,550*3,271,602
• T(3)=P(-3)Q(-3)= -5,757,369*5,335,266

P(-3), Q(-3), P(2), Q(2) などの大きさに注意してください。 これらはすべて約n/r=24/4=6桁の数字である。 6桁のものもあれば、7桁のものもある。

これまでのところ、私たちはこの問題を以下のステップ、またはアルゴリズムに減らしてきました：

(1) まずP(0), Q(0), P(1), Q(1), などを計算（低コストアクション）

(2) 2r-1=7 の T(x) の値を得るために、今度は約 n/r桁長の2r-1の数を掛け合わせなければなりません。 すなわち、P(0)Q(0), P(1)Q(1), P(-1)Q(-1), などを計算しなければならない。 (高コストアクション)

(3) データポイントからT(x)を再構築する。 (ローコストアクション)

(4) 再構築したT(x)を使って、この場合T(10⁶)を評価する

これにより、このアプローチの実行時間の分析がうまくいきますね。

実行時間

以上から、低コストのアクション(1)と(3)を一時的に無視すると、Toomのアルゴリズムで二つのn桁の数字を掛けるときのコストは以下のようになることがわかりました：

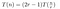
これは作業例で見た通りですね。 P(0)Q(0), P(1)Q(1), などをそれぞれ掛けるには、長さが約n/rの2つの数を掛けるので、T(n/r)のコストがかかります。 T(x) – 位数2r-2の多項式 – を2r-1箇所で標本化したいので、これを2r-1回行わなければなりません。 この種の方程式は明示的に解くことができます。

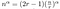
残るは 面倒な代数学

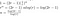
この他にも行列の乗算（再構成）処理でコストがかかっているので、その辺を説明する。 と足し算から、我々の解が正確な実行時間であるとは言えないので、代わりに実行時間の big-O を見つけたと結論づける

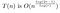
Optimising r

この実行時間はまだ r に依存します。 rを修正すれば完了です。 つまり、n の異なる値に対して変化する r の値を選びたいのです。

ここで重要なのは、r が変化する場合、再組み立てコストにいくらか注意を払う必要があることです – この操作を実行する行列は O(r²) のコストを持っているのです。 rが固定されているときは、それを見る必要はありませんでした。rを固定したままnが大きくなると、必要な計算量の増加を決定するのはnを含む項だからです。 r の最適な選択は n が大きくなるにつれて大きくなるので、もはやこれを無視することはできません。

この区別は非常に重要です。 当初、私たちの分析は r の値、おそらく 3、おそらく 30 億を選び、その後 n が任意に大きくなったときの big-O サイズを調べました。 今、私たちは、n が任意に大きくなり、r が私たちが決めたある割合で n と共に成長するときの振る舞いを見ています。 この視点の変更は、O(r²) を変数として見るもので、一方、r が固定されていたとき、O(r²) は、わからないとはいえ、定数でした。

そこで、以前からの分析を更新します：

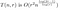
ここで O(r²) とは再構成マトリックスのコストになります。 我々は、今、この式をほぼ最小化するnの各値のrの値を選びたいのです。 最小化するために、まずrに関して微分してみます。すると、

通常は最小点を見つけるために微分を0に設定しますが、この式には良い最小点がありません。 代わりに、「十分な」解を見つけます。 r = r^(sqrt(logN)) を推定値として使用します。 図式的には、これは最小値にかなり近いです。 (下の図では、1/1000 の要因はグラフを適度なスケールで見えるようにするためにあります)

下のグラフは T(N) の関数を定数でスケーリングしたものを赤で表示しています。 緑色の線は x = 2^sqrt(logN) で、これは我々の見積もり値でした。 x」は「r」の代わりで、3枚の写真のそれぞれで、異なる値のNが使用されています。

これは、私たちの選択が正しかったことをかなり納得させるものです。 この r の選択で、それをプラグインし、我々のアルゴリズムの最終的な big-O:

ここで我々は単に r の値をプラグインし、大きな値の r に対して非常に正確である log(2r-1)/log(r) の近似を使っています。

How Much of An Improvement?

私が幼い頃に掛け算をしていたときにこのアルゴリズムに気付かなかったのは、おそらく妥当なことだったのでしょう。 下のグラフでは、big-O 関数の係数を 10 とし (デモンストレーションのため)、それを x² で割っています (乗算の元のアプローチは O(n²) であったため)。 赤線が 0 に傾く場合、新しい実行時間が漸近的に O(n²) よりも優れていることを示します。

そして実際、関数の形状は私たちのアプローチが最終的に速く、最終的にははるかに速くなることを示しますが、そうなるには 400桁近くも長い数字まで待つ必要があります! 9197>

10歳の私にとって、400桁の数字を掛けるのはちょっと無理がありますね！(笑) 私の関数のさまざまな再帰的呼び出しを追跡することも、少々大変なことです。 しかし、AI や物理学のタスクを行うコンピューターにとっては、これはよくある問題です！

この結果はどれほど深いものでしょうか？

このテクニックについて私が気に入っている点は、それがロケット科学ではないことです。 発見されたばかりの最も気の遠くなるような数学ではありません。 後から考えると、おそらくそれは明白に見えるでしょう！

しかし、これは数学の輝きと美しさなのです。 コルモゴロフがセミナーで、乗算は基本的に O(n²) であると推測した、という話を読んだことがあります。 コルモゴロフは、基本的に現代の確率論や解析学をたくさん発明しています。 20世紀を代表する数学者の一人です。 しかし、この無関係な分野に関しては、発見されるのを待っている知識の全体像が、彼や他のすべての人の鼻の下に置かれていることが判明しました！

実際、Divide and Conquerアルゴリズムは非常によく使われているので、今日かなりすぐに思いつきます。 しかし、これはコンピュータ革命の産物であり、膨大な計算能力を持つようになって初めて、それ自体で研究する価値のある数学の領域として、計算の速度に特別な焦点を当てたのです。 素晴らしい数学の世界は、常に我々の予想を裏切る能力を保持しているのです。

実際、乗算をさらに速くする方法を見つけることができます。 現在の最良のアプローチは、高速フーリエ変換を使用することです。 しかし、それはまた別の日にしましょう。

下にあなたの考えを聞かせてください。

私はこの問題を、物理学者ムーアとメルテンスによる「計算の本質」という素晴らしい本で知りました。