「彼らは数学を知っています。 ただ、単語問題ができないだけなのです。 それは読解力です」
Hartwell さんは、なぜ生徒たちが州のテストで苦労したかを説明していました。 彼女は生徒のことをよく知っていて、十分な評価をしていました。 彼女は、彼らの困難が識字能力の問題であることを確信していました。 子供たちはすでに国語のテストを受けているのです」
私は、数学の成績を上げるためのニューヨーク市のプログラムの一環として、ハートウェルさん（と彼女の学校の他の生徒）とマッチングされました。 その目的は、「Tier 1」の学校に概念的な数学を導入することでした。 Tier1とは、3つの分野で市をリードしている学校です。
私は、このプログラムの他の教師から「リテラシー」の説明を聞いたことがあります。 そして、それは理にかなっていました。 生徒が数学を知っているなら、なぜ単語問題の多いテストで苦労していたのでしょうか。
しかし、引っ掛かりがありました。 過去3年間で、識字能力は市全体で30%から40%になりました。 同じ期間、数学のスコアはほとんど横ばいだった。
これが読解の問題であれば、読解のスコアが上がれば、数学の爆発的な伸びを引き出すことができるはずです。
次の時間、私はハートウェル先生のクラスを訪問することになりました。
Over-Scaffolding Word Problems
生徒は丸テーブルに座り、彼女は一番前に立っていた。 彼女も生徒もみんな手持ちのホワイトボードを持っていました。
生徒たちは教科書の47ページを開き、彼女はある語句の問題を読み上げました。 「サラは馬のために40ポンドのニンジンを持っています。 もし彼女が100頭の馬を持っているとしたら、1頭の馬は何ポンドもらえるか？”
「OKクラス、彼女は各馬に与える40ポンドを持っています。 では、どのような操作が必要でしょうか？”
彼女は各操作の「キーワード」を列挙したアンカーチャートを指差しました。 各」は分割リストの一番上にありました。
「分割！」とクラスは答えました。 では、小さな数を大きな数で割るにはどうすればよいのでしょうか」
クラスは静かになった。 ハートウェル先生はホワイトボードにヴィンキュラム（長い割り算の家）を描きました。 ハートウェル先生が家の下に40、外に100を置くと、生徒たちは真似をしました。
「さて、100は40に入らないので、小数を加えなければなりません。 彼女は40を40.0に変更しました。 “100が400に入るのは何回でしょう？”
数人の生徒から “4！”という声が上がりました。
“Exactly. さて、商にも小数を入れる必要があります。
クラスはホワイトボードから「0.4」という答えを読み上げました。
彼女は同様の問題を出し、壁の「CUBES」ポスターを指差しました。 「数字を丸で囲み、キーワードを囲むことを忘れないでください」
彼女は生徒が作業している間、巡回していました。 ある者は、小数をどこに置くか質問しました。 他の人は、長い割り算の引き算の部分を並べるのに苦労していました。 レッスンが終わるころには、全員が正しい答えを紙に書いていました。 「ほらね。 これは極端な例ですが、ハートウェルさんが犯した間違いの多くは、実はかなり一般的なものです。 教育者が学生に「必要なだけ」サポートを提供することに誇りを持つのはよくあることですが、オーバー・スキャフォールドは違います。 彼は “Zone of Proximal Development” という造語を作りました。 ZPDには、学習者の手が届かないところにあるものが含まれます。 自分一人ではとてもできないが、サポートがあればできるようになる。 7769>
よく見落とされるのは、足場は学習者のZPDにすでにあるスキルにのみ適用されるということです。 現在、学習者の手の届かないところにあるスキルがたくさんあるのです。 7769>
過剰な足場固めの問題点の1つは、ターゲットとなるスキルを学生が決して内面化しないことである。 ZPDの範囲外のことで学生を助けると、その学生は常に私たちの助けを必要とします。
もう1つの問題は、過剰な叱責が誤った成功感を与えてしまうことです。 この場合、ハートウェルさんは、生徒が言葉の問題で「計算ができる」と信じていました。 しかし、実際には、生徒たちは彼女の動作を真似していただけでした。 7769>
彼女はまた、問題解決のプロセスから「定式化」の全プロセスを削除した。 多くの教育者は、理解と定式化を同じものと考えているが、定式化は別の数学的能力である。
そして、それはちょうどあなたが現在行っている単語問題の教え方に欠けている成分かもしれません。
教室リソースとプロフェッショナル学習
-
数学教室リソース2桁と3桁の数 with Base-10 ブロック｜インタラクティブなデジタル視覚モデル
$3.00カートに入れる
-
Math Classroom ResourcesCombining Like Terms with Algebra Tiles｜Interactive Digital Visual Models
$3.00カートに入れる
-
Math Classroom ResourcesDecimals with Base-10 Blocks to the Tenth and Hundredths | Digital Visual Models
$3.Add to cart.カートに入れる
-
Math Classroom ResourcesIntro to Algebra Tiles | Interactive Digital Visual Models
$3.00Add to cart
Formulation.Of.Unity
Math Classroom Resources
Intro to Algebra Tiles | Digital Visual Models$4.00Add to cart 単語問題で成功するための鍵
単語問題を定式化するには、それを理解することが必要です。 しかし、それはその先にあるものです。
生徒が言葉の問題を読むとき、まず、文字を音に変換しなければならない（デコーディング）。 次に、単語の意味を理解する必要があります（語彙）。 そして、その単語が文の中でどのように組み合わされているかを理解する必要があります（シンタックス）。 7769>
ほとんどの6年生がハートウェルさんの問題を読んで、サラが馬にニンジンを配っていることを簡単に理解することができた。 しかし、ニンジンを「分け与える」ことと割り算を結びつける人は、はるかに少ないでしょう。
この部分が、多くの教育者をつまずかせる。 私たちにはとても当たり前のことに思えるのですが。 “彼女は文字通りニンジンを分けているのです。 どうしてそれが分割であることがわからないのだろう。”
彼らはそうしないだけです。 もしそうなら、数学の教室にキーワードの表がぶら下がっているのを見ることはないでしょう。 そして、すべては最初に操作を教えたときにさかのぼるのです。
なぜ生徒は定式化で苦労するのか
多くの学校の多くの教師は、数学はセンス形成の科目であると生徒に教えています。 しかし、他の学校では、数学は記憶の科目として教えられている。
「記憶することとしての数学」の例としては、生徒が数学の事実を暗記するときがあります。 しかし、アルゴリズムもまた、記憶することに関するものである。 47の上に120を乗せる。 足し算はこの手順で、引き算はこの手順で、掛け算はこの手順で。
生徒は、数字の大きさや操作の意味さえ理解せずに、これらの手順を繰り返すことができます。
概念から始めると（視覚モデルや数の文章を使って）、生徒は操作が何を意味するかを学びます。 アルゴリズムから始めると、生徒は演算を一連のランダムなステップと考えるようになる。 宿題で30回同じアルゴリズムを完成させます。 数字を変えても、プロセスは同じです。 7769>
What the Tests Tell Us About Reasoning
We could give our students 10 problems with the title “Division Word Problems”, to make easy.単語問題を与えて、生徒が簡単に理解できるようにする。 彼らは問題を読む必要さえないでしょう。 どの数字が除数で、どの数字が配当かを考える（または推測する）だけでよいのです。
しかし、生徒が州のテストを受けるとき、目標はより簡単にすることではありません。 目標は、彼らが自分で何ができるかを評価することだ。
テストメーカーは、どの演算を使うかを教えたがらない。 同じ問題に割り算と足し算のキーワードを入れたりもする。 “クラスには20人の生徒がいます。 各子供が3ドルを持っているとしたら、全部でいくら持っていますか？”
ですから、生徒が言葉の問題に苦労するときは、言葉の問題だけではありません。 それはたいてい、彼らが記憶によって計算をしているということです。 7769>
Students Need Strategies and Process to Solve Word Problems
CUBES のようなシステムの問題の一部は、それが戦略と称しているが、実際はプロセスであることです。 一度効率的なプロセスを特定すれば、あまり深く考えずに何度も繰り返すことができます。 アルゴリズムもプロセスだ。 昼食までの道のりを「背の高い人から低い人」へと並べるのと同じです。
戦略は違います。 戦略には深い理解が必要です。 そして、新しい状況で理解を適用する能力だ。
我々は、生徒が言葉の問題で遭遇するすべてのシナリオのために準備することはできない。 あるものは、今まで組み合わせたことのない異なる数学のスキルを組み合わせることを要求します。 あるいは、正しい解答を導き出すために、ステップの順序を変更する必要がある場合もあります。
次のように考えてみましょう：
100 人の生徒が参加する学校行事で 5 ガロンのジュースを用意します。 各カップが3オンスである場合、各生徒は何カップ飲むことができますか？
問題解決プロセスは、生徒がこの問題に取り組み始めるのを助けることができます。 “何が問われているのかを確認する” “どのような情報が与えられているかを考える”
しかし、実際に解くために教えられる決まったプロセスはないのです。 そこで登場するのが戦略です。 単位を変換する必要があるのです。 完全に割るのではなく、余りを使って割っていることを認識させる。 また、ジュースをコップに分けてから生徒の数で割るなど、操作の順番を変える必要があるでしょう。
そこに「コツ」はありません。 演算の意味を理解する必要があるのです。 数学はセンスメーキングの科目であることを理解する必要があります。 7769>
The Polya Process for Solving Word Problems
George Pólya は影響力のあるハンガリーの数学者で、スタンフォード大学の教授であり、どんな問題にも使えるプロセスを発見した。 彼の研究は、数え切れないほどの数学者や教育者に影響を与えましたが、ほとんどの人は彼の名前を知りません。
実際、CUBES や他のいわゆる問題解決戦略は、彼の研究に緩やかに基づいています。 問題は、それを単純化しようとすることです。 その過程で、深い思考に似たものはすべて取り除かれている。
ポーリアは、あらゆる問題は4つのステップで解決できると信じていました。 理解する」「計画する」「解決する」「反省する」です。 ポリアのオリジナルの4ステップのプロセスは、学校で使うのにちょうどいいと思う。
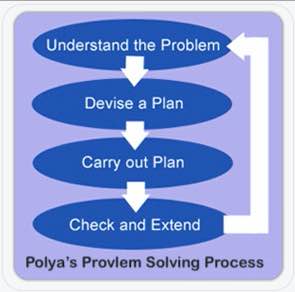問題を理解するために、どのような情報が与えられていて、何を見つけたいのかを明らかにする。 立方体の「C」と「U」はここから来ている。 生徒が数字に丸をつけ、問題に下線を引きたいなら、構いません。 私は、少なくとも最初は、グラフィック・オーガナイザーに（単位を付けて）書いてもらうことを希望します。 そうすることで、生徒が読んでいるものを処理しやすくなります。 また、教師である私が部屋の中を歩き回りながら、生徒の理解を評価するのにも役立ちます。 計画」は、問題を定式化するところです。 現実の世界のシナリオを、別の数学的表現に変えていくのです。
3つ目のステップは「解く」ことです。 正しく定式化できたなら、ここで計算をします。 学生は通常アルゴリズムを使用しますが、私は方程式や視覚的なモデルも使うことを推奨しています。
最後に、学生は自分の作品を振り返って確認します。 また、その過程を振り返ることも必要です。 もし間違いがあれば、それはなぜか？ 7769>
Strategies for Solving Word Problems
Word Problemsにアプローチするプロセスを持つことは、間違いなく役に立ちます。 しかし、ステップに従うだけで意味のある数学が身につくというふりをすることはできません。 単語問題の要点は、「数学の事実」とアルゴリズムを越えて数学を拡大することです。
定式化で生徒を助けるために、役に立つ戦略がいくつかあります。 最初は、いくつもの異なる戦略を明示的に教えます。
戦略を教えながら、その戦略と相性のよい問題を解かせるのです。 問題の種類によっては、「推測と確認」にとてもよく合うものがあります。 また、「絵を描く」に適しているものもあります。
最終的には、いくつかの方法で解くことができる難しい単語問題を与えます。 いったん道具立てを身につければ、状況に応じて最適なものを選べるようになる。 たとえば、絵を描くことは、しばしば処方を助けるのに役立ちます。 農家に18列のニンジンがあり、各列に10本のニンジンがあるとしたら、生徒はまず畑を描くことから始めるかもしれません。 ある時点で、「うわ、これは配列だ」と思い、暗算、式、またはアルゴリズムを使って掛け算できることに気づくかもしれません。
その他の場合、生徒は視覚モデルを使用して、問題を定式化し、解決することができます。
難しい言葉の問題に取り組む生徒を助ける
多くの先生方と同じように、生徒がこれらの問題にどう対処するのか心配になるかもしれません。 プロセス、ストラテジー、クリティカルシンキング……多くのことが関係しています。
この記事を読むまでは、単語問題は簡単そうだと思っていたかもしれません。
大切なのは、一度にすべてをやろうとして圧倒されないことです。 まずは簡単な単語問題をポリヤのプロセスで解くことから始めましょう。 そして、毎週新しいストラテジーを導入してください。 1年が終わるころには、彼らの成長ぶりに驚くことでしょう。
もしかしたら、創造的な問題解決について、もっと深く知りたいと考えているかもしれません。 7769>
明日から教室にポーリアを持ち込もうと思っているなら、このグラフィック・オーガナイザーはその手始めとして最適な方法です。 このグラフィックオーガナイザーは、4つのステップのプロセスの足場となり、生徒がどこで道を踏み外したかを特定するのに役立ちます。
Free Word Problem Organizer
About About Author
Jeff LisciandrelloはRoom to Discoverの創設者で、学生中心の学習を専門とする教育コンサルタントです。 彼の「3-Bridges Design for Learning」は、学校が伝統的な環境の中で革新的な実践を模索するのを支援します。 彼は、教育者が探究ベースの個別指導のアプローチを取り入れる手助けをすることに喜びを感じています。 Twitterでは、@EdTechJeff
と連絡を取ることができます。
単語問題を定式化するには、それを理解することが必要です。 しかし、それはその先にあるものです。
生徒が言葉の問題を読むとき、まず、文字を音に変換しなければならない（デコーディング）。 次に、単語の意味を理解する必要があります（語彙）。 そして、その単語が文の中でどのように組み合わされているかを理解する必要があります（シンタックス）。 7769>
ほとんどの6年生がハートウェルさんの問題を読んで、サラが馬にニンジンを配っていることを簡単に理解することができた。 しかし、ニンジンを「分け与える」ことと割り算を結びつける人は、はるかに少ないでしょう。
この部分が、多くの教育者をつまずかせる。 私たちにはとても当たり前のことに思えるのですが。 “彼女は文字通りニンジンを分けているのです。 どうしてそれが分割であることがわからないのだろう。”
彼らはそうしないだけです。 もしそうなら、数学の教室にキーワードの表がぶら下がっているのを見ることはないでしょう。 そして、すべては最初に操作を教えたときにさかのぼるのです。
なぜ生徒は定式化で苦労するのか
多くの学校の多くの教師は、数学はセンス形成の科目であると生徒に教えています。 しかし、他の学校では、数学は記憶の科目として教えられている。
「記憶することとしての数学」の例としては、生徒が数学の事実を暗記するときがあります。 しかし、アルゴリズムもまた、記憶することに関するものである。 47の上に120を乗せる。 足し算はこの手順で、引き算はこの手順で、掛け算はこの手順で。
生徒は、数字の大きさや操作の意味さえ理解せずに、これらの手順を繰り返すことができます。
概念から始めると（視覚モデルや数の文章を使って）、生徒は操作が何を意味するかを学びます。 アルゴリズムから始めると、生徒は演算を一連のランダムなステップと考えるようになる。 宿題で30回同じアルゴリズムを完成させます。 数字を変えても、プロセスは同じです。 7769>
What the Tests Tell Us About Reasoning
We could give our students 10 problems with the title “Division Word Problems”, to make easy.単語問題を与えて、生徒が簡単に理解できるようにする。 彼らは問題を読む必要さえないでしょう。 どの数字が除数で、どの数字が配当かを考える（または推測する）だけでよいのです。
しかし、生徒が州のテストを受けるとき、目標はより簡単にすることではありません。 目標は、彼らが自分で何ができるかを評価することだ。
テストメーカーは、どの演算を使うかを教えたがらない。 同じ問題に割り算と足し算のキーワードを入れたりもする。 “クラスには20人の生徒がいます。 各子供が3ドルを持っているとしたら、全部でいくら持っていますか？”
ですから、生徒が言葉の問題に苦労するときは、言葉の問題だけではありません。 それはたいてい、彼らが記憶によって計算をしているということです。 7769>
Students Need Strategies and Process to Solve Word Problems
CUBES のようなシステムの問題の一部は、それが戦略と称しているが、実際はプロセスであることです。 一度効率的なプロセスを特定すれば、あまり深く考えずに何度も繰り返すことができます。 アルゴリズムもプロセスだ。 昼食までの道のりを「背の高い人から低い人」へと並べるのと同じです。
戦略は違います。 戦略には深い理解が必要です。 そして、新しい状況で理解を適用する能力だ。
我々は、生徒が言葉の問題で遭遇するすべてのシナリオのために準備することはできない。 あるものは、今まで組み合わせたことのない異なる数学のスキルを組み合わせることを要求します。 あるいは、正しい解答を導き出すために、ステップの順序を変更する必要がある場合もあります。
次のように考えてみましょう：
100 人の生徒が参加する学校行事で 5 ガロンのジュースを用意します。 各カップが3オンスである場合、各生徒は何カップ飲むことができますか？
問題解決プロセスは、生徒がこの問題に取り組み始めるのを助けることができます。 “何が問われているのかを確認する” “どのような情報が与えられているかを考える”
しかし、実際に解くために教えられる決まったプロセスはないのです。 そこで登場するのが戦略です。 単位を変換する必要があるのです。 完全に割るのではなく、余りを使って割っていることを認識させる。 また、ジュースをコップに分けてから生徒の数で割るなど、操作の順番を変える必要があるでしょう。
そこに「コツ」はありません。 演算の意味を理解する必要があるのです。 数学はセンスメーキングの科目であることを理解する必要があります。 7769>
The Polya Process for Solving Word Problems
George Pólya は影響力のあるハンガリーの数学者で、スタンフォード大学の教授であり、どんな問題にも使えるプロセスを発見した。 彼の研究は、数え切れないほどの数学者や教育者に影響を与えましたが、ほとんどの人は彼の名前を知りません。
実際、CUBES や他のいわゆる問題解決戦略は、彼の研究に緩やかに基づいています。 問題は、それを単純化しようとすることです。 その過程で、深い思考に似たものはすべて取り除かれている。
ポーリアは、あらゆる問題は4つのステップで解決できると信じていました。 理解する」「計画する」「解決する」「反省する」です。 ポリアのオリジナルの4ステップのプロセスは、学校で使うのにちょうどいいと思う。
問題を理解するために、どのような情報が与えられていて、何を見つけたいのかを明らかにする。 立方体の「C」と「U」はここから来ている。 生徒が数字に丸をつけ、問題に下線を引きたいなら、構いません。 私は、少なくとも最初は、グラフィック・オーガナイザーに（単位を付けて）書いてもらうことを希望します。 そうすることで、生徒が読んでいるものを処理しやすくなります。 また、教師である私が部屋の中を歩き回りながら、生徒の理解を評価するのにも役立ちます。 計画」は、問題を定式化するところです。 現実の世界のシナリオを、別の数学的表現に変えていくのです。
3つ目のステップは「解く」ことです。 正しく定式化できたなら、ここで計算をします。 学生は通常アルゴリズムを使用しますが、私は方程式や視覚的なモデルも使うことを推奨しています。
最後に、学生は自分の作品を振り返って確認します。 また、その過程を振り返ることも必要です。 もし間違いがあれば、それはなぜか？ 7769>
Strategies for Solving Word Problems
Word Problemsにアプローチするプロセスを持つことは、間違いなく役に立ちます。 しかし、ステップに従うだけで意味のある数学が身につくというふりをすることはできません。 単語問題の要点は、「数学の事実」とアルゴリズムを越えて数学を拡大することです。
定式化で生徒を助けるために、役に立つ戦略がいくつかあります。 最初は、いくつもの異なる戦略を明示的に教えます。
戦略を教えながら、その戦略と相性のよい問題を解かせるのです。 問題の種類によっては、「推測と確認」にとてもよく合うものがあります。 また、「絵を描く」に適しているものもあります。
最終的には、いくつかの方法で解くことができる難しい単語問題を与えます。 いったん道具立てを身につければ、状況に応じて最適なものを選べるようになる。 たとえば、絵を描くことは、しばしば処方を助けるのに役立ちます。 農家に18列のニンジンがあり、各列に10本のニンジンがあるとしたら、生徒はまず畑を描くことから始めるかもしれません。 ある時点で、「うわ、これは配列だ」と思い、暗算、式、またはアルゴリズムを使って掛け算できることに気づくかもしれません。
その他の場合、生徒は視覚モデルを使用して、問題を定式化し、解決することができます。
難しい言葉の問題に取り組む生徒を助ける
多くの先生方と同じように、生徒がこれらの問題にどう対処するのか心配になるかもしれません。 プロセス、ストラテジー、クリティカルシンキング……多くのことが関係しています。
この記事を読むまでは、単語問題は簡単そうだと思っていたかもしれません。
大切なのは、一度にすべてをやろうとして圧倒されないことです。 まずは簡単な単語問題をポリヤのプロセスで解くことから始めましょう。 そして、毎週新しいストラテジーを導入してください。 1年が終わるころには、彼らの成長ぶりに驚くことでしょう。
もしかしたら、創造的な問題解決について、もっと深く知りたいと考えているかもしれません。 7769>
明日から教室にポーリアを持ち込もうと思っているなら、このグラフィック・オーガナイザーはその手始めとして最適な方法です。 このグラフィックオーガナイザーは、4つのステップのプロセスの足場となり、生徒がどこで道を踏み外したかを特定するのに役立ちます。
Free Word Problem Organizer
About About Author
Jeff LisciandrelloはRoom to Discoverの創設者で、学生中心の学習を専門とする教育コンサルタントです。 彼の「3-Bridges Design for Learning」は、学校が伝統的な環境の中で革新的な実践を模索するのを支援します。 彼は、教育者が探究ベースの個別指導のアプローチを取り入れる手助けをすることに喜びを感じています。 Twitterでは、@EdTechJeff
と連絡を取ることができます。