ケーキのように、小さいものを2個食べても、2倍のものを1個食べても、同じ量になります。 したがって、多くの分数は、2/5や4/10のように等価です。


どんな数も分数として書ける
分割されていない全体の部分の総数は1なので、1以上のどんな整数も分数になるように書きます。
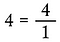
分数を真横に掛ける
分数の掛け算は簡単で真横に掛けるだけです。
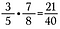
注:混合数はまず不適正分数にしなければならない、これについては続きを読んでください。
いつでもどんな形の1でもかける
数字の1は、どんな数でもかけることができ、その数は変わらないので、乗法的恒等式と呼ばれています。 これは分数にとって重要なことで、実際には値を変えずに分数の外観を変える必要があることがよくあるからだ。
たとえば、3/3を掛けることによって、1/3を等価な分数3/9に変えることができる。
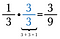
等しいサイズの部品を足したり引いたり
分数を足したり引いたりするには分母は同一でなければならない。 それは理にかなっています。
では、分数の大きさが同じでない場合はどうするのですか?
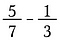
1の形で掛けると分母を共通の大きさに変更することができる。 基本的には、分数を同じ大きさになるまで小さく分割しているのです。 これを共通分母を求めるといいます。
本当は、どの共通分母でもよいのですが、人は最小のものを求めることを好みます。 この場合、7と3の両方が余りなく入る最小の数は21です。 そこで、最初の分数に3/3を、2番目の分数に7/7を掛けます。
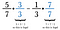
最小共通分母が思いつかない場合は、常に各分数に反対の額を掛けるとよいでしょう。 この場合のように、それが最小公倍数であることが判明することもあります。
分母が一致したら、分子を引いて8/21を求めます。
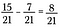
これは予想通りの結果になりました。

15個の青いブロックから、7個ずつ色付けを除去してください。

これで予想通り8/21が残る。
混合数を最初に変更
混合数とは整数と分数を組み合わせたもので、整数と分数が混在している場合。
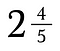
混合数は他の分数とはうまくかみ合わないのです。
注:不適切な分数とは、分子が分母より大きく、1より大きい値を持つ分数のことです。
混合数の変換は本当に足し算
2と4/5を不適切な分数に変換するには、2 + 4/5を加えます。
ステップ1:2を2/1と書き換えることからはじめます。
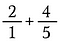
Step 2: 2/1 に 5/5 をかけて、希望の共通分母 5 を持つ 10/5 の等価分数にする。
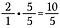
ステップ3: 10/5 + 4/5 を足し算する。
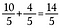
この結果は、同等の不等号14/5になります。
混合数に戻すには、割り算をして下さい。 例えば、5 は 14 に 2 回入り(5 x 2 = 10 なので)、4 個残ります。
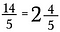
Compare fraction using the Cross Product
Such like to determine which is bigger.とすると、どちらが大きいか? 5/12と6/13です。
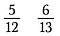
ステップ1.分数を比較する。 対角線を掛け、分子の上に積を書きます。
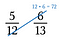
ステップ2. もう一方の対角線に掛け、その積を分子の上に書きます。
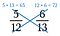
ステップ3:その積を分子とします。 製品を比較します。 積が大きい側が大きな分数になります。
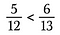
我々は、分数が同じかどうかを、交差積を使って判断することもできる。
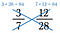
3/7と12/28の外積はともに84ですから、3/7=12/28です。
Cancel Anything That Divides to One
分数の良い点はキャンセルする機会をたくさん見つけられることです。 391>
例えば、8/10という分数があったとします。
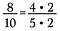
2/2 = 1なので、2を打ち消して、4/5になる分数を減らすと、8と10が書き直せる。
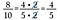
だから2の部分を消す、この作戦で分数の掛け算も簡単にできるようにしましょう。
各数値を因子で書き換えることから始めましょう。 例えば、5/5=1.
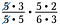
5のペアはもちろん、3のペアも同様に1割するものがありますね。
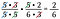
おっと! 6を2×3と書き換えて、2のペアをキャンセルすればよかったんだ。
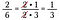
15/25×10/18を直接かけていたら、計算量が多くなってしまいますが、相殺を使うことで分数をあらかじめ減らして、かけ算を簡単にしています。
分数の割り算に乗算を使う
分数の割り算の考え方は、次のような簡単な例で簡単に理解できます:

全体の半分があるので、5の半分に10の半分がある。
しかし、この概念はより複雑な分数で厄介になる。
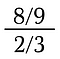
この問題を解くには、2つの事実を利用します:
- 1の任意の形式(すなわち。
- 3/2の逆数である2/3を掛けると、打ち消しによって1が得られます
ステップ1。
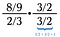
さて、解くべき二つの小さな問題があります(青と緑)。 一番下の(緑色の)分数で1になるものをすべてキャンセルします。

これで解くべき上の問題が残りました。
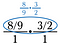
ステップ 3 です。 打ち消しを使って分数をあらかじめ減らしておく。 これらの削減を行った後、横にかけて4/3を求めます。

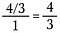
Shortcut
これは「反転してかける」のロングハンドのしくみです。”
底の逆数は常に1にキャンセルされるので、掛け算を省略できます。 したがって、分子に分母の逆数を掛けるだけです。

Bonus: Theory, in case you interested.
素晴らしい質問ですね!
この質問には答えられません。 一般化すると、a,b,c,dの文字を使って4種類の数を表す分数を2つ作ります。
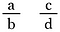
両方の分数にb〜dを掛けます(これで分母を相殺することができます)。
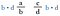
ここで左側のbと右側のdは割ると1なので打ち消しましょう。 分数はなくなり、d-aとc-bの積だけになりました。
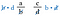
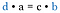
元の分数を見て下さい。 これは対角線にかけた場合と同じ積です。 したがって、十字積を比較するのが近道です。
❤ STAY CONNECTED ❤
Math Hacksのすべての最新情報を入手しましょう!
。