最近、同僚から「なぜこんなに活性化関数があるんですか?「とか、「どの関数を使えばいいかわかるのか」とか、「筋金入りの数学なのか」とか。 そこで、ニューラルネットワークを基本的なレベルでしか知らない人、したがって、活性化関数とその「なぜなぜ数学!」について疑問に思っている人のために、この記事を書いてはどうかと考えました。
活性化関数
では、人工の神経細胞は何をするのでしょうか。 簡単に言えば、入力の「重み付き和」を計算し、バイアスを加えて、「発火」させるかどうかを決めるのです(そう、活性化関数がこれを行うのですが、ちょっと流れに任せてみましょうか)。
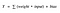
ここで、Y は -inf から +inf までの値を取ることができます。 ニューロンは本当に値の境界を知らないのです。 では、どのようにしてニューロンが発火すべきかどうかを決定するのでしょうか(なぜこの発火パターンなのでしょうか? そのために「活性化関数」を追加することにしました。 ある神経細胞が出すY値を調べて、外部の接続がこの神経細胞を「発火した」とみなすかどうかを決定するためです。
ステップ関数
最初に思いついたのは、閾値ベースの活性化関数はどうだろうということでした。 Yの値がある値以上であれば、活性化したと宣言します。 もし閾値より小さければ、そうでないと言う。 うーん、素晴らしい。 これは使えるかも!
活性化関数 A = “activated” if Y > threshold else not
あるいは、A = 1 if y> threshold, 0 otherwise
さて、今やったのは「ステップ関数」、下図をご覧ください。
出力は値> 0(しきい値)のとき1(アクティブ)、それ以外は0(非アクティブ)を出力する
素晴らしい。 これでニューロンの活性化関数ができましたね。 混乱はありません。 しかし、これにはある欠点があります。
例えば、2値分類器を作成するとします。 はい」または「いいえ」(アクティブまたは非アクティブ)と言うべきものです。 Step 関数はそれを行うことができます。 さて、このようなニューロンを複数接続して、より多くのクラスを持ってくるようなユースケースを考えてみましょう。 クラス1、クラス2、クラス3などです。 1つ以上のニューロンが「活性化」されるとどうなるでしょうか。 全てのニューロンは1(ステップ関数より)を出力します。 さて、何を判断するのでしょうか? どのクラスでしょうか?
ネットワークが 1 つのニューロンだけを活性化し、他のニューロンは 0 になるようにしたいでしょう(そうして初めて、正しく分類した、クラスを識別したと言えるのです)。 ああ!この方法では、学習と収束が難しくなります。 活性化を2値化せず、「50%活性化」「20%活性化」等とした方が良かったかもしれません。
この場合も、1つ以上のニューロンが「100%活性化」と言えば、まだ問題は残っていますね。 しかし、出力に中間活性化値があるため、学習がスムーズで簡単になり、学習中にステップ関数と比較して、1つ以上のニューロンが100%活性化する可能性が低くなります (また、学習内容やデータにもよりますが)。
最初に思いつくのは一次関数でしょう。
一次関数
A = cx
入力(ニューロンからの加重和)に比例して活性化する直線関数です。 いくつかのニューロンを接続し、1つ以上の発火があれば、最大値(またはソフトマックス)を取り、それに基づいて決定することができるのは確かです。 だからそれもOK。
学習用の勾配降下法に慣れている人なら、この関数では微分が定数であることに気づくでしょう。
A = cx, x に関する微分は c。つまり、勾配は X とは関係がないのです。 予測に誤差があっても、逆伝播による変化は一定で、入力の変化 delta(x) に依存しない !!!
これはあまり良くない!!!! (常にというわけではありませんが、ご容赦ください)。 もう一つ問題があります。 接続された層について考えてみましょう。 各層は一次関数で活性化される。 その活性化は入力として次の層に入り、2層目はその入力の重み付き和を計算し、今度は別の線形活性化関数に基づいて発火する。
何層あっても、すべてが線形であれば、最終層の活性化関数は1層目の入力の線形関数に過ぎない
つまり、この 2 つの層 (または N 個の層) は 1 つの層で置き換えることができるのです。 あ!この方法でレイヤーを積み重ねる機能を失っただけです。 どう重ねてもネットワーク全体は線形活性化(線形関数の線形的な組み合わせはやはり別の線形関数)の単層と等価なのです。
次にいきましょうか。
シグモイド関数
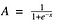
さてこれはなめらかで「ステップ関数っぽい」感じですな。 これの利点は何でしょうか。 ちょっと考えてみてください。 まず第一に、非線形であること。 この関数の組み合わせも非線形です 素晴らしい。 これでレイヤーを重ねることができますね。 非二値活性化はどうだろう? それもそうだ! ステップ関数と違って、アナログな活性化ができる。 また、勾配も滑らかです。
そして、X値-2から2の間で、Y値が非常に急になっていることにお気づきでしょうか。 つまり、その領域でXの値を少し変化させると、Yの値が大きく変化します。
この関数は、Y値を曲線のどちらかの端に寄せる傾向があるということですね。 はい、そうです。 活性値を曲線のどちらかに寄せる傾向があります(例えば、x = 2以上、x = -2以下)。
この活性化関数のもう一つの利点は、線形関数と違って、活性化関数の出力が常に(0,1)の範囲になることです。 つまり、活性化関数はある範囲に束縛されているのです。 いいね、これなら活性化関数が爆発することはない。 シグモイド関数は、現在最も広く使われている活性化関数の1つです。
Sigmoid 関数の両端では、X の変化に対する Y 値の反応が非常に小さくなる傾向があることに気づきました。 その領域での勾配が小さくなってしまうのです。 それは「消失勾配」という問題を生じさせます。 ふむ。 では、活性度が曲線の左右の「水平に近い部分」付近に達するとどうなるか。
Gradient is small or has vanished (cannot make significant change because of the extremely small value). ネットワークがそれ以上の学習を拒否するか、極端に遅くなる (ユースケースによって、また、勾配/計算が浮動小数点値の制限にヒットするまでに)。 この問題を回避する方法があり、シグモイドは分類問題でいまだに非常に人気がある。
Tanh Function
もうひとつの活性化関数として、tanh 関数が使用されることがある。
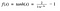
ふーん。 これはsigmoidとよく似ていますね。 実際、これはスケールされたシグモイド関数です!

OK、今度はこれは上で説明したシグモイドに似た特徴を持っていますね。 これは非線形で、層を重ねることができます。 これは範囲(-1, 1)に束縛されているので、活性化が爆発する心配はありません。 一点、シグモイドよりもtanhの方が勾配が強いです(微分が急)。 シグモイドとtanhのどちらを選択するかは、勾配の強さの要件に依存します。 シグモイドと同様、tanhにも消失勾配の問題があります。
Tanhも非常に有名で広く使われている活性化関数です。 xが正ならx、そうでなければ0を出力します。
一見、正軸に線形なので線形関数と同じ問題があるように見えますが、実は、この関数は、正軸に線形であることが重要です。 まず、ReLuはもともと非線形である。 そして、ReLuの組み合わせも非線型です! (そして、ReLuの組み合わせも非線形です!(実は良い近似器なのです。 どんな関数もReLuの組み合わせで近似することができる)。 素晴らしい、つまりこれはレイヤーを重ねることができるということです。 しかし、それは束縛されるものではありません。 ReLuの範囲は[0, inf]です。
もう一つ、活性化の疎密について説明します。 多くのニューロンを持つ大きなニューラルネットワークを想像してみてください。 シグモイドやtanhを使用すると、ほとんどすべてのニューロンがアナログ的に発火することになります(覚えていますか)。 つまり、ほとんどすべての活性化がネットワークの出力を記述するために処理されることになる。 言い換えれば、活性化は密である。 これはコストがかかります。 理想的には、ネットワーク内の少数のニューロンは活性化しないようにし、それによって活性化を疎にし、効率的にすることです。 ランダムな重みの初期化(または正規化)されたネットワークで、ReLuの特性(xの負の値に対して0を出力)により、ネットワークのほぼ50%が0活性となることを想像してみよう。 これは、発火するニューロンの数が少なく(疎な活性化)、ネットワークが軽くなることを意味する。 うぉー、すごい ReLuってすごいんだね! そうなんです、でも完璧なものなんてないんです。
ReLuの水平線(負のXの場合)は、勾配が0になることがあります。 つまり、その状態になったニューロンは誤差や入力の変動に反応しなくなる(単に勾配が0だから何も変わらない)。 これはReLu問題(Dying ReLu Problem)と呼ばれる。 この問題により、いくつかのニューロンはただ死んでしまい、反応しなくなり、ネットワークのかなりの部分が受動的になってしまう。 ReLuにはこの問題を軽減するために、水平線を非水平成分にするバリエーションがある。例えば、x<0に対してy = 0.01xは水平線ではなく、わずかに傾いた線になる。 これがリーキーReLuである。 このほかにもいろいろなバリエーションがある。 主なアイデアは、勾配をゼロ以外にし、最終的に学習中に回復させることです。
ReLu は tanh や sigmoid よりも簡単な数学演算を含むので、計算コストが低くなります。
Ok, now, which do we use?
さて、どの活性化関数を使うか。 すべて ReLu を使用すればよいということでしょうか。 それともシグモイドやタンを使うのでしょうか。 まあ、イエスでもありノーでもあります。 近似しようとする関数がある特性を持っていることが分かっている場合、その関数をより速く近似する活性化関数を選択することで、より速い学習プロセスを実現することができます。 例えば、シグモイドは分類器に適しています(シグモイドのグラフを見てください、理想的な分類器の特性を示していると思いませんか? なぜなら,分類器の関数をシグモイドの組み合わせで近似することは,例えば ReLu などよりも簡単だからです. これにより,学習過程と収束が速くなります. 独自のカスタム関数を使用することもできます。 もし、学習しようとしている関数の性質がわからないのであれば、ReLuから始めて、その後に逆戻りすることをお勧めします。 ReLuはほとんどの場合、一般的な近似関数として機能します!
この記事では、一般的に使用されるいくつかの活性化関数について説明しようとしました。 他の活性化関数もありますが、一般的な考え方は変わりません。 よりよい活性化関数のための研究はまだ進行中です。 活性化関数の背後にある考え方、なぜそれが使われるのか、どのように使うのかを理解していただければ幸いです。