ニューマンプロジェクタのR/S配置の決定
どのようにしてニューマンプロジェクタのR/S配置を決めるのでしょう?
では、どのようにニューマンプロジェクタを線分図に変換すればよいのでしょうか。
目次
- Newman Projectionsで(R)と(S)を決定する。 4253>
- Most people are actually OK at visualizing Familiar Things in 3-D. 有機化学の初心者の問題は、分子がなじみがないことです
- 猫はなじみ深いものです。 そこで、猫の「ニューマン予想図」を描いてみましょう
- ニューマン・プロジェクション 4253>
- Eclipsed and Staggered Conformations Are Interconverted by Rotation of 60° Along the Central C-C Bond
- How To Convert A Newman Projection To A Line Diagram
- A Cheat Sheet for Going From A Newman To A Line Diagram: 考慮すべきテンプレートは 4 つだけ
- Newman Projection で R と S の配置を決定する。 例1
- ニューマン プロジェクションにおける R と S の配置を決定する。 例2
- Newman Eclipsed Conformation の R と S を決定する。 例3.
- 結論。 Newman Projection の R と S の配置を決定する
1. Newman Projectionsでの(R)と(S)の決定
最近の2つの投稿では、Cahn-Ingold-Prelog (CIP) 規則を使って、単純なものも複雑なものも含めて、様々な状況でキラルカーボンの配位に(R/S)を割り振る方法について述べました。
これまでの問題では、左下の分子のような結合線図として描かれた分子に対して、(R/S)を割り当てることが求められてきました。 しかし、たまには、たとえば試験のように、ヒントヒント、ループに陥ることがあるかもしれません。 たとえば、分子がニューマンとして描かれているとき、R/Sはどのように決定するのでしょうか。 (右下)
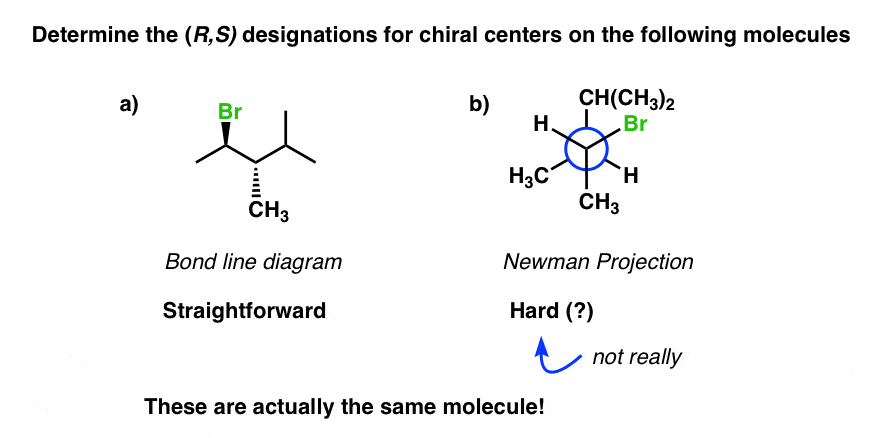
そのコツは、Newman の投影図をボンドライン図に変換してから R/S を割り当てることです。
この投稿は Organic Chemistry Solutions の Matt Pierce との共同執筆でした。 このような場合、「痒いところに手が届く」「痒いところに手が届く」「痒いところに手が届く」「痒いところに手が届く」「痒いところに手が届く」「痒いところに手が届く」。 このような場合、「曖昧さ」をなくすことが重要です。 有機化学を始める人にとっての問題は、分子が馴染みのないものであるということです
有機化学が難しい理由について学生からよく聞くのは、「3Dで物事を視覚化するのが難しい」ということです。
実はこれは真実ではないと思います。
ほとんどの人は3Dで物を視覚化して問題ないでしょう。
この仮説に基づき、身近なものを取り上げて視覚化の練習をしてみましょう。
ここに、空腹のエルサレムのストリート キャットの写真があります。

横から見るとどう見えるかを視覚化できますか。
ほぼ間違いなく、あなたはほとんどの角度から猫がどのように見えるかをよく知っているからです。
もしあなたが絵を描くとしたら(棒グラフでも構いません)、おそらく次のようになるでしょう:
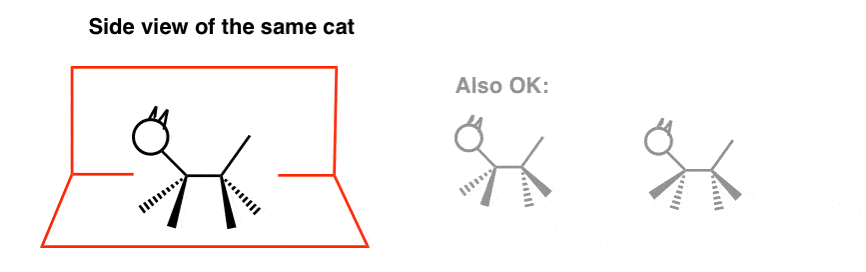
私たちはいくつかの自由を得たことに注意してください。
ここで、同じような練習を逆にしてみましょう。
先ほど描いた棒人間を、前から(つまり左から見て)、後ろから(右から見て)どう見えるかを思い描いてみましょう。
すぐに明らかになる理由ですが、少し詳細を追加します。猫に色のついた「靴下」(オレンジと青)を履かせます。 簡単のために、目の描画は省略しました。
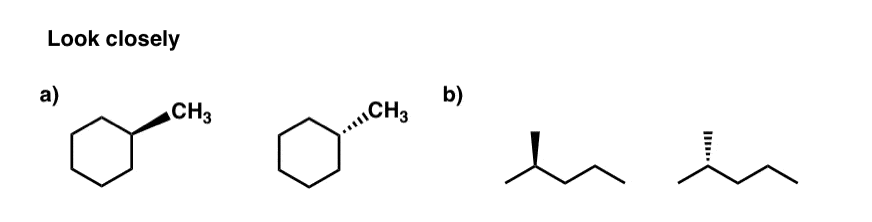
円は猫の体を表しており、前と後ろの腰が互いにブロックしているからです。
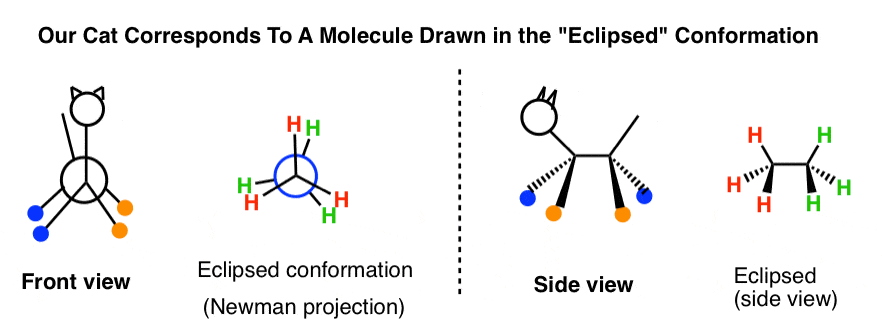
もうひとつ注目すべきは「スタッガード」で、前の3グループが後ろの3グループに対して60度ずれている。
5. 中心炭素-炭素結合に沿って60度回転させると、食刻型と千鳥型が相互変換する
下の例では、後ろの炭素を前の炭素に対して時計回りに60度、中心炭素-炭素結合に沿って回転させます。 この後、緑の水素がそれぞれ12時から2時、4時から6時、8時から10時に移動したことに注目してください。
この「千鳥足」分子を横から見ると、ページの平面上の結合がジグザグの配置になっている結合線図(右下)を得ることができます。
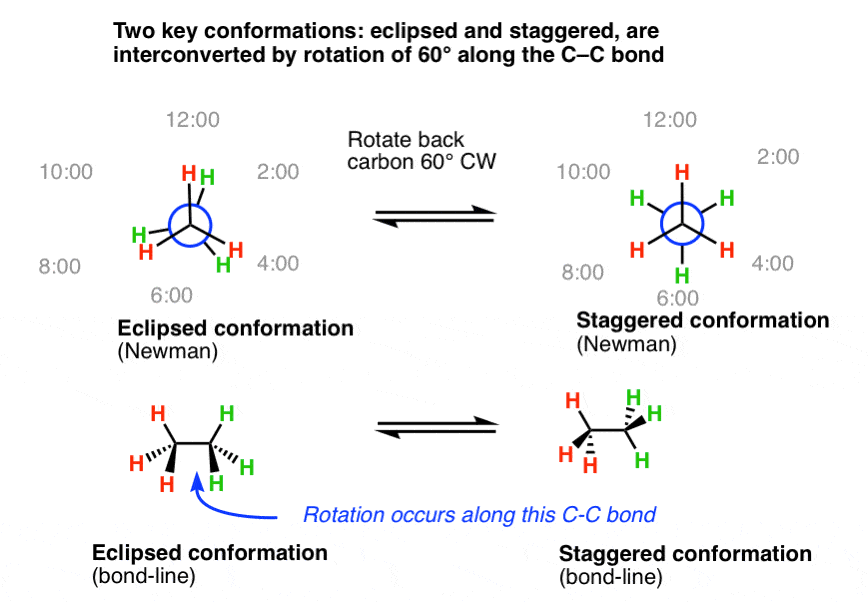
この「千鳥」結合線図を左から見ると、右上に描いた「千鳥」ニューマンが得られる。
6. ニューマン図を線分図に変換する方法
では、ニューマン図をボンド線分図に変換するにはどうしたらよいでしょうか。
最初に認識すべきことは、ボンドライン図では、ページの平面上の結合が従うパターンは4つしかないことです。
「千鳥配置」に対応する「ジグザグ」形と、「食刻配置」に対応する「C形」の2つの可能性があります。 .
これらの4つの線図パターンをそれぞれ左から見ると、それぞれが異なるニューマン投影パターンを生成していることがわかります。
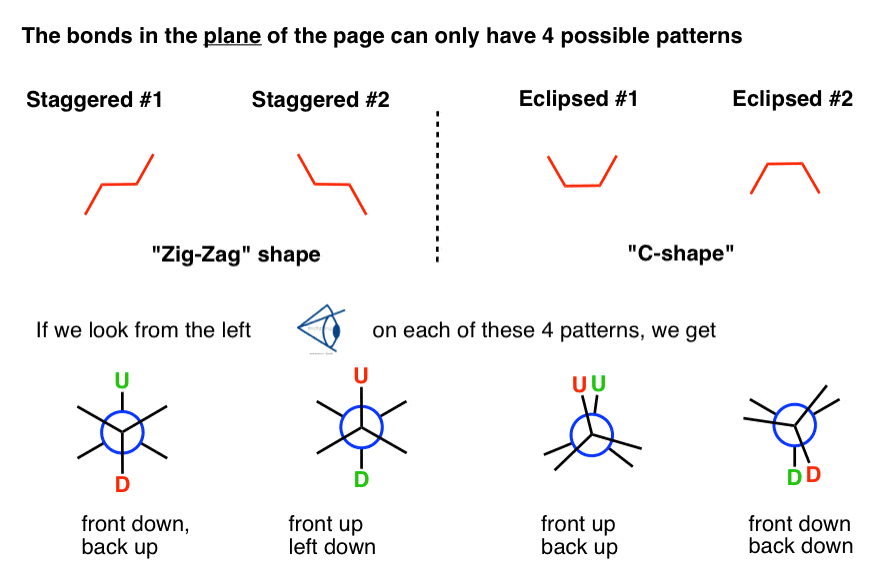
順方向でのパターンの働きを見たので、今度は逆方向でこれらのパターンを適用してみましょう。
7.ニューマンから線分図にするためのチートシート。 3520>
これらのテンプレートを使って、任意のニューマン・プロジェクションを逆算して、対応するボンドラインのテンプレートを見つけ、ダッシュとウェッジを描き込んでいくことができます。 (右側は30°傾けたときの様子)。 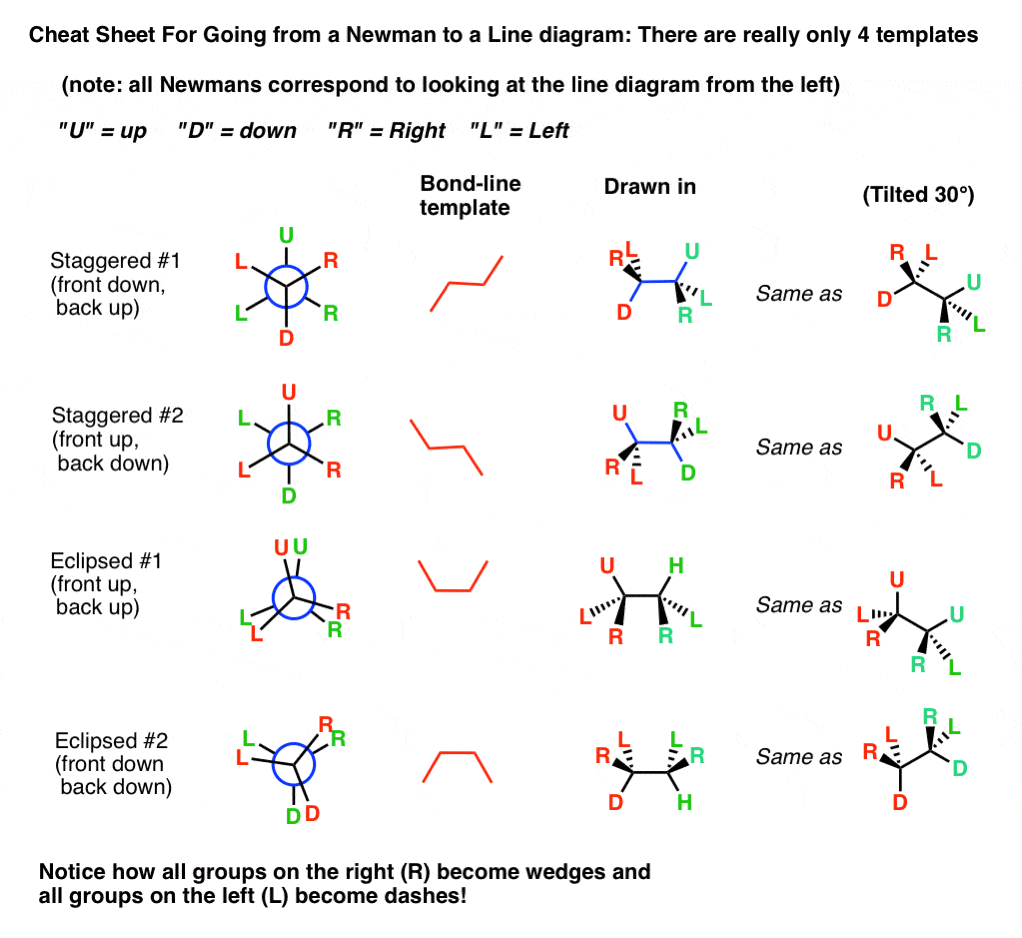
一つ重要なことがあります。 猫の時もそうでしたが、分子の左側から見ると、
- 右側(R)の基はすべてくさびになり、
- 左側(L)の基はすべてダッシュになります
左から見るというパターンでいけば、あとはニューマン図の右側でくさびの描き方を覚えれば良いのです。
8.ニューマン図上でのRとSの配置の決定。 例1
これをいくつかの具体例に当てはめてみましょう。
まず、立体中心が1つの千鳥配置で描いたニューマンにR/Sを割り当ててみましょう。
これは (front up, back down) と描かれているので、上のテンプレート 2 を使用します。
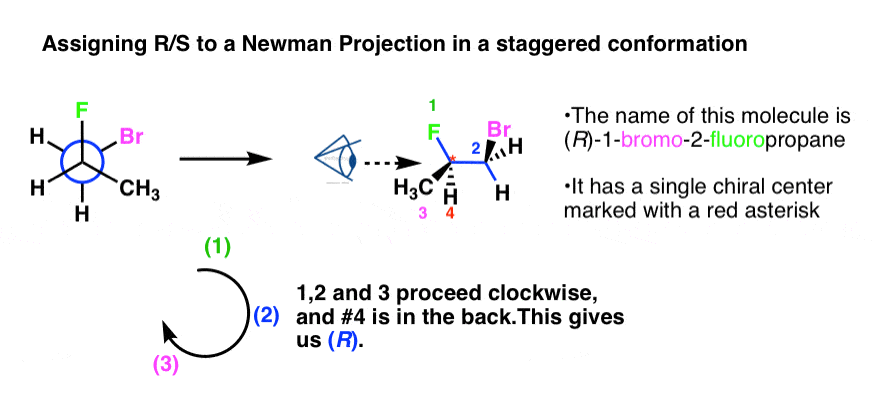
この例では、(front up, back down) staggered template を描き、それから結合を塗りつぶしました。 Newmanの右側の基(BrとCH3)は線図では楔になったことに注意してください。
配置としては(R)が得られるはずです。 Newmanの射影でRとSの配置を決定する。 例2
次に、元の例(2-ブロモ-3,4-ジメチルペンタン)に戻ってやってみましょう。
これも千鳥配置(前が下、後ろが上)で描かれていますね。 そこで、ここではテンプレート#1を使用します。
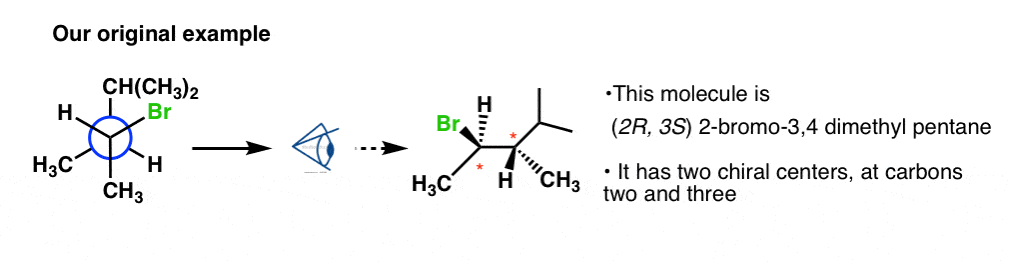
同じ方法で、Brを含む立体中心は(R)、炭素3番の立体中心は(S)を求めればよいのです。 この方法の詳細は画像をご覧ください。
10. 日食のあるニューマンでRとSを決定する。 例3.
もし分子が食錐台になっていたらどうでしょうか。
これは(前下がり、後ろ下がり)パターンなので、テンプレート#4
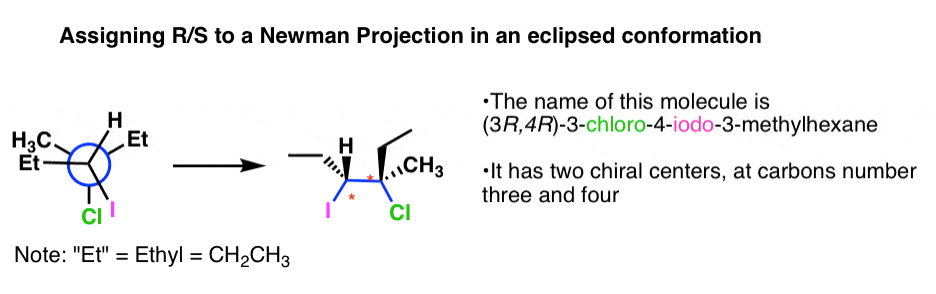
(3R, 4R)が得られるはずです。 その方法の詳細は、こちらをご覧ください。
結論です。 ニューマン予想図におけるRとSの配置の決定
猫を正面から見たときと横から見たときがイメージできれば、ニューマン予想図を線分図に変換することができるはずです。 これは、Newman projection で R/S を決定する最初のステップです。
テンプレートがいくつかあることを知っていると、簡単にできます。
何度もやっていると、テンプレートも必要なくなり、頭の中でやるほうが簡単だと思うかもしれません。