グラフには、頂点の数、辺の数、相互接続性、全体の構造によって様々な種類があります。 8085>
Null Graph
辺を持たないグラフをNull Graphと呼びます。
例

上のグラフでは、a、b、cという3頂点がありますが、それらの間には辺が存在しません。
Trivial Graph
頂点が1つしかないグラフをTrivial Graphと呼ぶ。
例
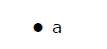
上のグラフでは頂点はaだけで、他の辺がない。
無向グラフ
無向グラフには辺があるが、有向ではない辺がある。
例
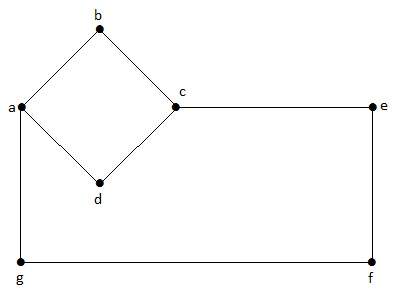
このグラフで、’a’, ‘b’, ‘c’, ‘d’, ‘e’, ‘f’, ‘g’ は頂点、’ab’, ‘bc’, ‘cd’, ‘da’, ‘ag’, ‘gf’, ‘ef’ はグラフ上の辺である。 無向グラフなので、辺’ab’と’ba’は同じである。
有向グラフ
有向グラフでは、各辺には方向がある。
例
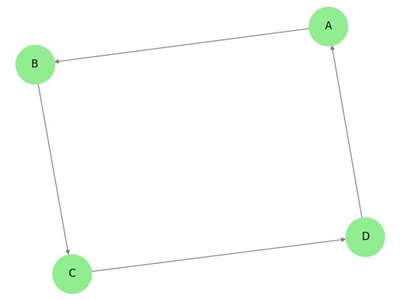
上のグラフでは、7つの頂点’a’, ‘b’, ‘c’, ‘d’, ‘e’, ‘f’, ‘g’ と、8つの辺 ‘ab’, ‘cb’, ‘dc’, ‘ad’, ‘ec’, ‘fe’, ‘gf’, ‘ga’ を持っています。 有向グラフであるため、各辺にはその方向を示す矢印マークがついている。 8085>
単純グラフ
ループや平行辺がないグラフを単純グラフと呼ぶ。
-
頂点が「n」個のグラフで可能な辺の最大数はnC2(nC2=n(n – 1)/2)である。
-
「n」個の頂点を持つ単純なグラフの数=2nc2=2n(n-1)/2。
例
次のグラフでは3頂点、3辺で、並行辺とループを除くと最大です。 8085> 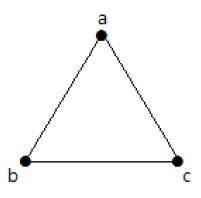
頂点がn=3のときの辺の最大数 –
nC2 = n(n–1)/2 = 3(3–1)/2 = 6/2 = 3 edges
頂点がn=3の単純グラフの最大数 –
2nC2 = 2n(n-1)/2 = 23(3-1)/2 = 23 = 8
これらのグラフは以下の8つである。 グラフの各頂点には少なくとも1本の辺があるはずである。
例題
次のグラフでは,各頂点はそれぞれ他の辺に接続された辺を持っている.
Disconnected Graph
グラフGが少なくとも2つの連結頂点を含まないとき、それは切断されています。
例1
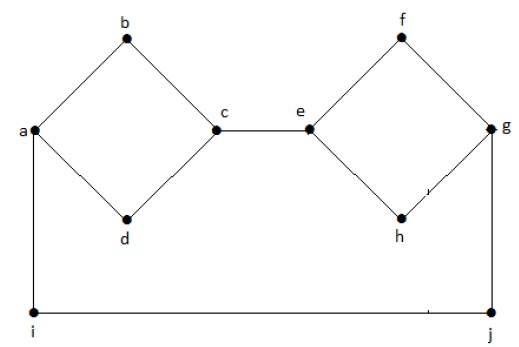
次のグラフは切断グラフの例で、’a’, ‘b’, ‘c’, ‘d’ 頂点を持つ成分と ‘e’, ‘f’, ‘g’, ‘h’ 頂点を持つ成分の二つが存在する場合。 したがってdisconnected graphと呼ばれる。
例2
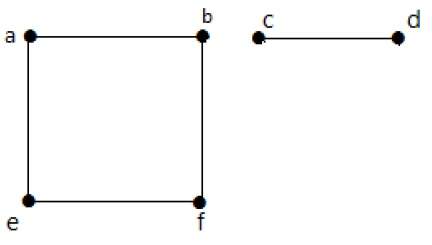
この例では、a-b-f-eとc-dという二つの独立した成分があり、これらは互いに接続されていない。
正則グラフ
グラフGは、すべての頂点の次数が同じであれば、正則であるといいます。 グラフにおいて、各頂点の次数が「k」であるとき、そのグラフは「k-正則グラフ」と呼ばれる。
例
次のグラフでは、すべての頂点が同じ次数である。
いずれのグラフも頂点の次数は2である。
完全グラフ
頂点が相互に’n’個ある単純なグラフを完全グラフと呼び,’Kn’で表す.
言い換えれば、ある頂点が他のすべての頂点とつながっているグラフを完全グラフと呼ぶ。
例
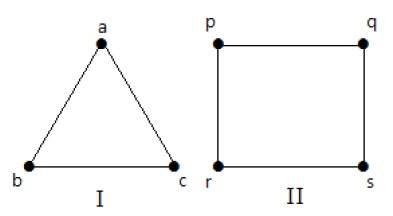
以下のグラフでは、グラフ中の各頂点は自分以外の残りのすべての頂点とつながっている。
グラフIの場合。
| a | b | c | |
|---|---|---|---|
| a | 未接続 | 接続済み | |
| b | Connected | Not Connected | |
| c | Connected | Not Connected |
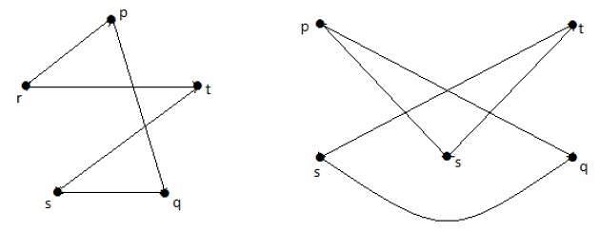
グラフIIにおいて、
を選択。
| p | q | r | s | |
|---|---|---|---|---|
| p | 接続されていない | 接続された | Connected6783 | Connected |
| q | Connected | Not Connected | ||
| r | Connected | 接続中 | 未接続 | |
| S | 接続中 | 接続中 | 未接続 |
Cycle Graph
頂点が ‘n’ (n >= 3) で辺が ‘n’ の単純グラフは、すべての辺が長さ ‘n’ のサイクルを形成するとき、サイクルグラフと呼ばれます。
グラフの各頂点の次数が2であれば、サイクルグラフと呼ぶ。
表記 – Cn
例
次のグラフを見てみよう。
グラフIIは4頂点4辺でサイクル「pq-qs-sr-rp」を形成。
グラフIIIは5頂点5辺でサイクル「ik-km-ml-lj-ji」を形 成する。
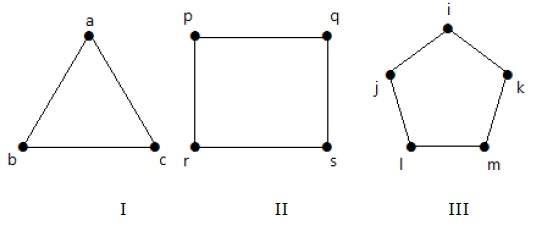
したがって、与えられたグラフはすべてサイクルグラフである。
車輪グラフ
車輪グラフはサイクルグラフCn-1から新しい頂点を加えて得られるものである。 その新しい頂点をハブと呼び、Cnのすべての頂点に接続する。
Notation – Wn
No. of edges in Wn = No. of edges from hub to all other vertices + No. of edges from all other nodes in cycle graph without a hub. = (n–1) + (n–1) = 2(n–1)
Example
次のグラフを見てみよう。 8085> 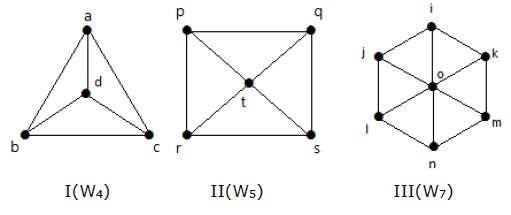
グラフIは、C3から真ん中のdという頂点を加えたものである。 グラフIIでは、C4から真ん中にtという頂点を加えて、W4とする。 グラフIIIでは、C6から中央にoという頂点を加えてW5.
Number of edges in W5 = 2(n-1) = 2(4) = 8
とする。 8085>
Number of edges in W4 = 2(n-1) = 2(6) = 12
Cyclic Graph
少なくとも1つのサイクルを持つグラフをcyclic graphと呼ぶ。
例
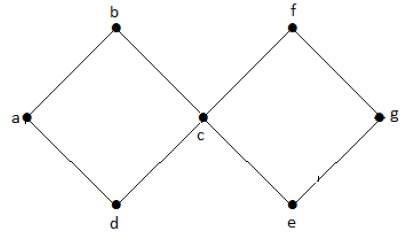
上の例のグラフにはa-b-c-d-a と c-f-g-e-c があり、サイクルは2つである.
Acyclic Graph
サイクルのないグラフをacyclic graphと呼ぶ。
例
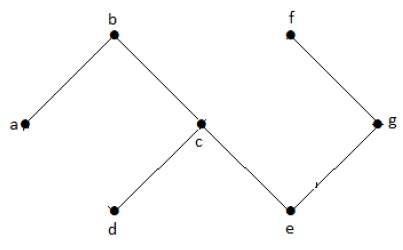
上のグラフ例ではサイクルがない.
2部グラフ
頂点分割V={V1, V2}の単純グラフG = (V, E)は、Eのすべての辺がV1の頂点とV2の頂点を結ぶとき2部グラフと呼ばれます。
一般にバイパーティットグラフは2組の頂点(V1とV2)を持ち、辺を描けばV1の任意の頂点とV2の任意の頂点を結ぶはずです。
例
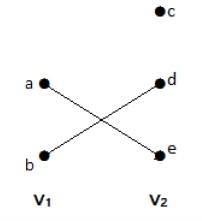
このグラフではV1とV2という二つの頂点の集合を見ることができます。 ここで、’ae’と’bd’という2本の辺が2組の頂点V1とV2を結んでいる。
完全2-部グラフ
2-部グラフ ‘G’, G = (V, E) で分割 V = {V1, V2} はV1中のすべての頂点がV2中のすべての頂点とつながっていれば完全2部グラフと呼ばれる。
一般に完全2-部グラフは集合V1からの各頂点と集合V2からの各頂点を結ぶ。
例
次のグラフは集合V1から集合V2までの各頂点を結ぶ辺があるので完全2-部グラフである。
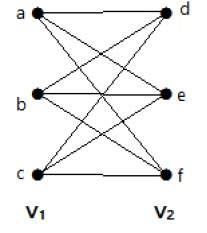
|V1|=m、|V2|=nならば完全2-部グラフは Km, n で示される。
-
Km,n は (m+n) 頂点と (mn) 辺を持つ。
-
Km,n はm=nなら正則グラフ。
一般に、完全2部グラフは完全グラフではない。
Km,n はm=nなら完全グラフとなる。
頂点数nの2-部グラフの最大辺数は
n=10のとき。 K5, 5= ⌊n2/4⌋ = ⌊102/4⌋ = 25
同様に K6, 4=24
K7, 3=21
K8です。 2=16
K9, 1=9
n=9とすると、k5、4=⌊n2/4⌋=⌊92/4⌋=20
同様にk6, 3=18
K7, 2=14
K8, 1=8
‘G’ が奇数長のサイクルを持たないとき、’G’ は2-部グラフになる。 8085>
Star Graph
K1, n-1の形の完全な2-部グラフはn-頂点を持つスターグラフである。 星型グラフは1つの頂点が一方の集合に属し、残りのすべての頂点が他方の集合に属するとき、完全2部グラフとなる。
例
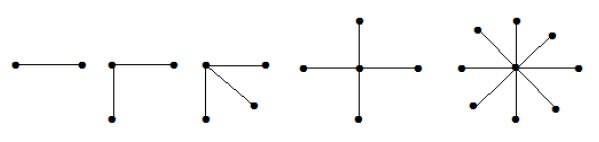
上のグラフでは、「n」の頂点のうち、「n-1」の頂点はすべて1つの頂点とつながっている。
グラフの補集合
ある頂点をGとし、辺{U, V}がGに存在しない場合、G-に存在する単純グラフがG-であるとする。
グラフIに存在する辺が別のグラフIIに存在せず、グラフIとグラフIIの両方を合わせて完全なグラフにする場合、グラフIとグラフIIは互いに補集合と呼ばれる。
例
次の例で、グラフIには2本の辺’cd’と’bd’がある。 その補集合であるグラフ-IIには4本の辺がある。
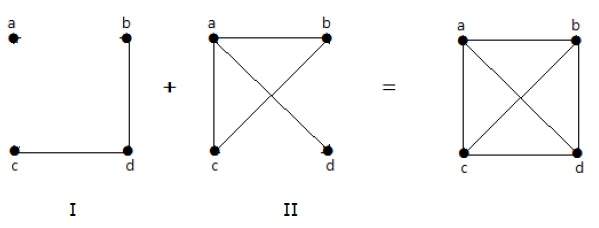
グラフ-Iの辺はグラフ-IIには存在せず、その逆もまた然りであることに注意せよ。
注-2つの補グラフの組み合わせは完全グラフを与える。
Gを任意の単純グラフとすると、
|E(G)| +|E(‘G-‘)| =|E(Kn)|, ここにnはグラフの頂点の数である。
例題
‘G’を9個の頂点と12個の辺を持つ単純グラフとすると、’G-‘の辺の数を求めよ。
あなたは、|E(G)|+|E(G-)|=|E(Kn)|
12 + |E(’G-‘)| =
とすることができた。