幾何学では、平行四辺形、ひし形、正方形、長方形、台形、カイトなど多くの種類の四辺形があって、共通する性質があるので理解に苦しむことがあるようですが、このような図形を理解している人は少ないでしょう。 ひし形は、隣接する辺が等しい斜めの正方形と言える。
ひし形と平行四辺形の基本的な違いは、ひし形のすべての辺が同じ長さであるのに対し、平行四辺形は対辺が平行である直線的な図形である、という特性にあります。 ひし形対平行四辺形
- 比較表
- 定義
- 主な違い
- 結論
比較表
比較の根拠
ひし形
平行四辺形
意味
ひし形とは、平たい形のことを指す。 四辺が合同である図形。
平行四辺形とは、四辺が平行な平面図形です。
等辺
四辺はすべて同じ長さを持っています。
対角線
対角線は直角に二等分し、スカレン三角形を形成します。
面積
(pq)/2, ここでpとqは対角線
bh, b =底辺とh =高さ
周囲
4 a, a =辺
2 (a+b), ここでa＝辺、b＝底辺
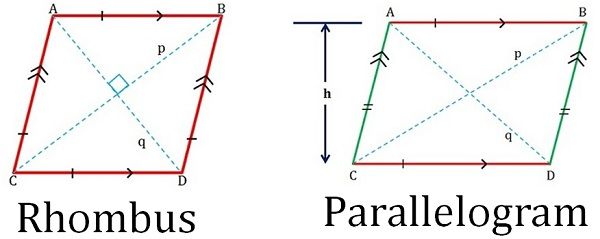
ひし形の定義
辺の長さが合同な四角形をひし形と呼びます。 ひし形は平らで、4つの側面があり、向かい合った側面は互いに平行です（下図参照）。 対角線は90度(直角)で交わるので、互いに垂直で、2つの正三角形になる。 隣接する辺は補角であり、それらの測定の和が180度に等しいことを意味する。 8033>
Definition of Parallelogram
A parallelogram is a flat shaped figure, having four sides whose set of opposite sides are parallel and congruent (see figure given below).
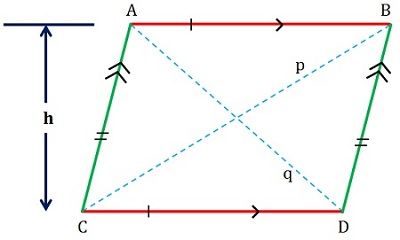The measure of its facing angles is equal and consecutive angles are supplemental, すなわちthe sum of their measure equal to 180 degrees.It is also known as an equilateral parallellogram.
[平行四辺形を表す名称が示すように]この図形は、対角が平行で合同でありながら4つの辺を持つ平面図形として表される。
Key Differences Between Rhombus and Parallelogram
Rhombus とParallelogram の違いは、以下の理由で明確に描くことができます：
- Rhombus を平らな形、四辺形の四辺形のすべての面の長さが一致していると定義します。
- ひし形のすべての辺の長さが等しいのに対し、平行四辺形の辺の長さが等しいのは反対側の辺だけである。 対角線が2つの合同三角形を形成する平行四辺形とは対照的です。
- ひし形の面積の数式は、pとqを対角線とすると、（pq）/2です。 逆に、平行四辺形の面積は底辺と高さの掛け算で計算できる。
- ひし形の周囲は次の公式を参考にして計算できる-4 a、ここでaはひし形の辺である。 逆に、平行四辺形の周囲は、底辺と高さを足して、その和に2をかければ計算できます。
結論
平行四辺形もひし形も、向かい合った辺が平行で、対角が等しくて内角の和が360度である四角形です。 ひし形はそれ自体が特殊な平行四辺形である。 したがって、すべてのひし形は平行四辺形であると言えるが、その逆はありえない
。