Ci sono vari tipi di grafi a seconda del numero di vertici, numero di bordi, interconnettività, e la loro struttura generale. In questo capitolo discuteremo solo alcuni importanti tipi di grafi.
Grafico Nullo
Un grafico che non ha bordi è chiamato Grafico Nullo.
Esempio

Nel grafico sopra, ci sono tre vertici chiamati ‘a’, ‘b’, e ‘c’, ma non ci sono bordi tra loro. Quindi è un grafico Null.
Grafico Triviale
Un grafico con un solo vertice è chiamato un grafico Triviale.
Esempio
Nel grafico mostrato sopra, c’è solo un vertice ‘a’ senza altri bordi. Quindi è un grafico banale.
Grafico non diretto
Un grafico non diretto contiene bordi ma i bordi non sono diretti.
Esempio
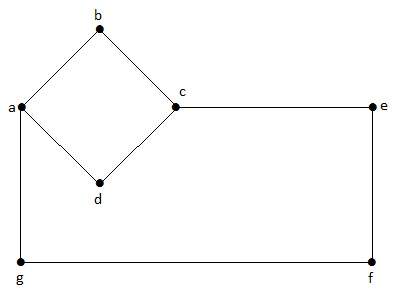
In questo grafico, ‘a’, ‘b’, ‘c’, ‘d’, ‘e’, ‘f’, ‘g’ sono i vertici, e ‘ab’, ‘bc’, ‘cd’, ‘da’, ‘ag’, ‘gf’, ‘ef’ sono i bordi del grafico. Poiché è un grafo non diretto, i bordi ‘ab’ e ‘ba’ sono uguali. Allo stesso modo anche gli altri bordi sono considerati allo stesso modo.
Grafico diretto
In un grafico diretto, ogni bordo ha una direzione.
Esempio
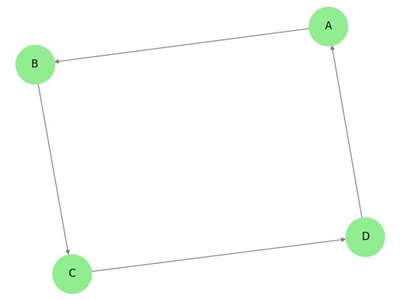
Nel grafico sopra, abbiamo sette vertici ‘a’, ‘b’, ‘c’, ‘d’, ‘e’, ‘f’, e ‘g’, e otto bordi ‘ab’, ‘cb’, ‘dc’, ‘ad’, ‘ec’, ‘fe’, ‘gf’, e ‘ga’. Dato che è un grafo diretto, ogni bordo porta una freccia che mostra la sua direzione. Nota che in un grafo diretto, ‘ab’ è diverso da ‘ba’.
Grafico semplice
Un grafico senza loop e senza bordi paralleli è chiamato grafico semplice.
-
Il numero massimo di bordi possibili in un singolo grafico con ‘n’ vertici è nC2 dove nC2 = n(n – 1)/2.
-
Il numero di grafi semplici possibili con ‘n’ vertici = 2nc2 = 2n(n-1)/2.
Esempio
Nel seguente grafico, ci sono 3 vertici con 3 bordi che è massimo escludendo i bordi paralleli e i loop. Questo può essere dimostrato usando le formule precedenti.
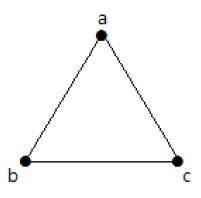
Il numero massimo di bordi con n=3 vertici –
nC2 = n(n–1)/2 = 3(3–1)/2 = 6/2 = 3 edges
Il numero massimo di grafi semplici con n=3 vertici –
2nC2 = 2n(n-1)/2 = 23(3-1)/2 = 23 = 8
Questi 8 grafi sono come mostrato di seguito –
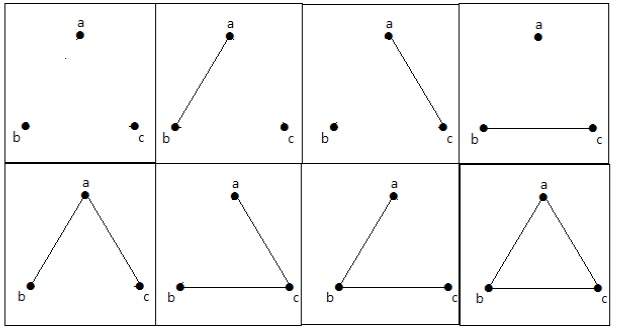
Grafico connesso
Un grafico G è detto connesso se esiste un percorso tra ogni coppia di vertici. Ci deve essere almeno un bordo per ogni vertice del grafico. Così possiamo dire che è connesso a qualche altro vertice dall’altra parte del bordo.
Esempio
Nel seguente grafico, ogni vertice ha il suo bordo connesso ad un altro bordo. Quindi è un grafico connesso.
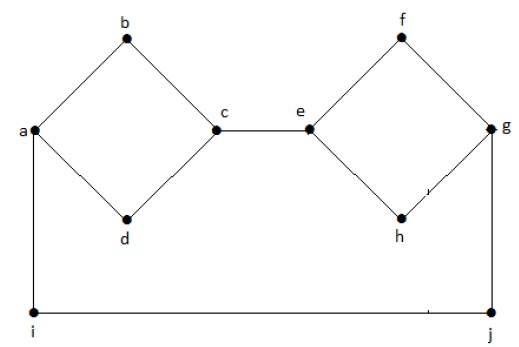
Grafico sconnesso
Un grafico G è sconnesso, se non contiene almeno due vertici connessi.
Esempio 1
Il seguente grafico è un esempio di Grafo Disconnesso, dove ci sono due componenti, uno con vertici ‘a’, ‘b’, ‘c’, ‘d’ e un altro con vertici ‘e’, ‘f’, ‘g’, ‘h’.
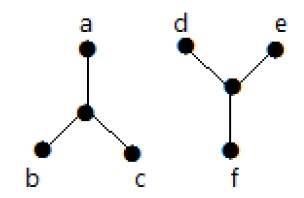
I due componenti sono indipendenti e non connessi tra loro. Quindi è chiamato grafo disconnesso.
Esempio 2
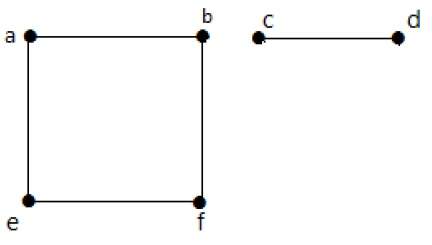
In questo esempio, ci sono due componenti indipendenti, a-b-f-e e c-d, che non sono connessi tra loro. Quindi questo è un grafo disconnesso.
Grafo regolare
Un grafo G si dice regolare, se tutti i suoi vertici hanno lo stesso grado. In un grafico, se il grado di ogni vertice è ‘k’, allora il grafico è chiamato ‘grafico k-regolare’.
Esempio
Nei seguenti grafici, tutti i vertici hanno lo stesso grado. Quindi questi grafi sono chiamati grafi regolari.
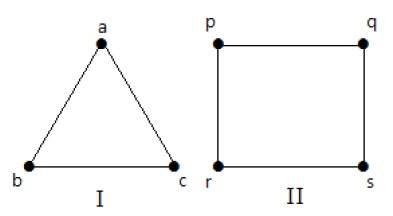
In entrambi i grafi, tutti i vertici hanno grado 2. Sono chiamati grafi 2-Regolari.
Grafo completo
Un grafo semplice con ‘n’ vertici reciproci è chiamato un grafo completo ed è denotato da ‘Kn’. Nel grafico, un vertice deve avere bordi con tutti gli altri vertici, allora si chiama un grafico completo.
In altre parole, se un vertice è collegato a tutti gli altri vertici in un grafico, allora si chiama un grafico completo.
Esempio
Nei seguenti grafici, ogni vertice del grafico è collegato con tutti i restanti vertici del grafico tranne se stesso.
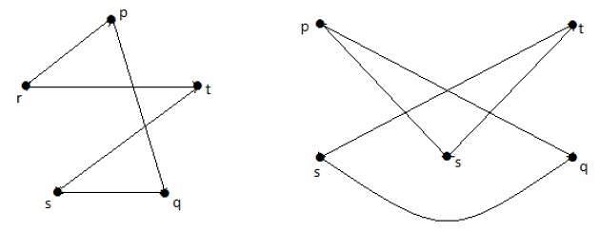
Nel grafico I,
| a | b | c | |
|---|---|---|---|
| a | Non Connesso | Connesso | Connesso |
| b | Connesso | Non connesso | Connesso |
| c | Connesso | Connesso | Non connesso |
Nel grafico II,
| p | q | r | s | |
|---|---|---|---|---|
| p | Non Connesso | Connesso | Connesso | Connesso |
| q | Connesso | Non Connesso | Connesso | Connesso |
| r | Connesso | Connesso | Non collegato | Connesso |
| s | Connesso | Connesso | Connesso | Non Connesso |
Grafico a ciclo
Un grafo semplice con ‘n’ vertici (n >= 3) e ‘n’ bordi si chiama grafico a ciclo se tutti i suoi bordi formano un ciclo di lunghezza ‘n’.
Se il grado di ogni vertice del grafico è due, allora si chiama Grafo Ciclo.
Nota – Cn
Esempio
Guarda i seguenti grafici –
-
Il grafico I ha 3 vertici con 3 bordi che formano un ciclo ‘ab-bc-ca’.
-
Il grafico II ha 4 vertici con 4 bordi che formano il ciclo ‘pq-qs-sr-rp’.
-
Il grafico III ha 5 vertici con 5 bordi che formano il ciclo ‘ik-km-ml-lj-ji’.
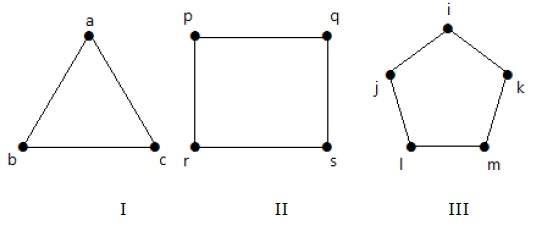
Quindi tutti i grafi dati sono grafi di ciclo.
Grafico a ruota
Un grafico a ruota si ottiene da un grafico a ciclo Cn-1 aggiungendo un nuovo vertice. Questo nuovo vertice è chiamato Hub che è connesso a tutti i vertici di Cn.
Notazione – Wn
No. of edges in Wn = No. of edges from hub to all other vertices + No. of edges from all other nodes in cycle graph without a hub. = (n–1) + (n–1) = 2(n–1)
Esempio
Guarda i seguenti grafici. Sono tutti grafici a ruota.
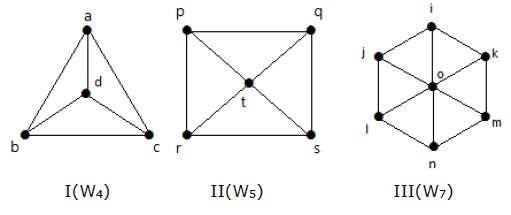
Nel grafico I, è ottenuto da C3 aggiungendo un vertice al centro chiamato ‘d’. È indicato come W4.
Number of edges in W4 = 2(n-1) = 2(3) = 6
Nel grafico II, è ottenuto da C4 aggiungendo un vertice al centro chiamato ‘t’. È indicato come W5.
Number of edges in W5 = 2(n-1) = 2(4) = 8
Nel grafico III, è ottenuto da C6 aggiungendo un vertice al centro chiamato ‘o’. È indicato come W7.
Number of edges in W4 = 2(n-1) = 2(6) = 12
Grafico ciclico
Un grafico con almeno un ciclo è chiamato grafico ciclico.
Esempio
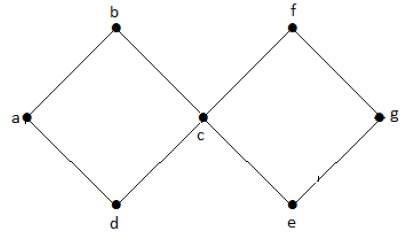
Nel grafico di esempio sopra, abbiamo due cicli a-b-c-d-a e c-f-g-e-c. Quindi è chiamato un grafico ciclico.
Grafico aciclico
Un grafico senza cicli è chiamato un grafico aciclico.
Esempio
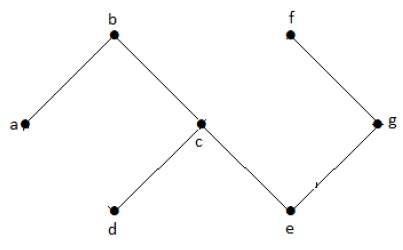
Nel grafico di esempio sopra, non abbiamo alcun ciclo. Quindi è un grafo non ciclico.
Grafo bipartito
Un grafo semplice G = (V, E) con partizione dei vertici V = {V1, V2} è detto grafo bipartito se ogni bordo di E unisce un vertice di V1 a un vertice di V2.
In generale, un grafo bipartito ha due insiemi di vertici, diciamo V1 e V2, e se un bordo è disegnato, dovrebbe collegare qualsiasi vertice nell’insieme V1 a qualsiasi vertice nell’insieme V2.
Esempio
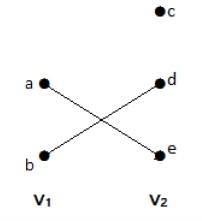
In questo grafico, puoi osservare due insiemi di vertici – V1 e V2. Qui, due bordi chiamati ‘ae’ e ‘bd’ stanno collegando i vertici di due insiemi V1 e V2.
Grafico bipartito completo
Un grafico bipartito ‘G’, G = (V, E) con partizione V = {V1, V2} si dice che è un grafico bipartito completo se ogni vertice di V1 è collegato ad ogni vertice di V2.
In generale, un grafo bipartito completo collega ogni vertice dell’insieme V1 a ogni vertice dell’insieme V2.
Esempio
Il seguente grafico è un grafo bipartito completo perché ha bordi che collegano ogni vertice dell’insieme V1 a ogni vertice dell’insieme V2.
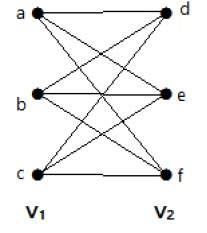
Se |V1| = m e |V2| = n, allora il grafico bipartito completo è indicato con Km, n.
-
Km,n ha (m+n) vertici e (mn) bordi.
-
Km,n è un grafo regolare se m=n.
In generale, un grafo bipartito completo non è un grafo completo.
Km,n è un grafico completo se m=n=1.
Il numero massimo di bordi in un grafo bipartito con n vertici è
Se n=10, k5, 5= ⌊n2/4⌋ = ⌊102/4⌋ = 25
Similmente K6, 4=24
K7, 3=21
K8, 2=16
K9, 1=9
Se n=9, k5, 4 = ⌊n2/4⌋ = ⌊92/4⌋ = 20
Similmente K6, 3=18
K7, 2=14
K8, 1=8
‘G’ è un grafico bipartito se ‘G’ non ha cicli di lunghezza dispari. Un caso speciale di grafo bipartito è un grafo a stella.
Grafico a stella
Un grafo bipartito completo della forma K1, n-1 è un grafo a stella con n vertici. Un grafo a stella è un grafo bipartito completo se un singolo vertice appartiene a un insieme e tutti i restanti vertici appartengono all’altro insieme.
Esempio
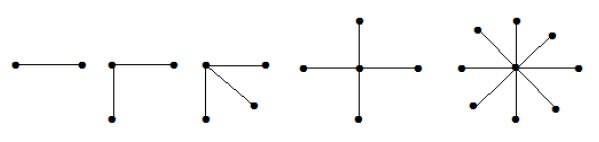
Nei grafi precedenti, su ‘n’ vertici, tutti gli ‘n-1’ vertici sono connessi a un singolo vertice. Quindi è nella forma di K1, n-1 che sono grafi a stella.
Complemento di un grafo
Sia ‘G-‘ un grafo semplice con alcuni vertici come quello di ‘G’ e un bordo {U, V} è presente in ‘G-‘, se il bordo non è presente in G. Significa, due vertici sono adiacenti in ‘G-‘ se i due vertici non sono adiacenti in G.
Se i bordi che esistono nel grafico I sono assenti in un altro grafico II, e se sia il grafico I che il grafico II sono combinati insieme per formare un grafico completo, allora il grafico I e il grafico II sono detti complementi l’uno dell’altro.
Esempio
Nel seguente esempio, il grafico I ha due bordi ‘cd’ e ‘bd’. Il suo complemento graph-II ha quattro bordi.
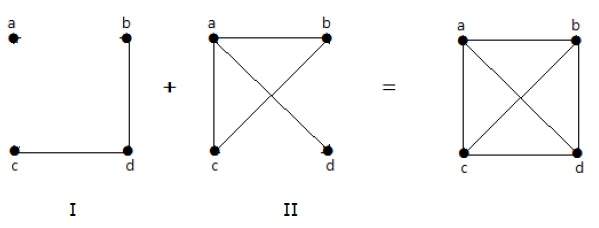
Nota che i bordi nel graph-I non sono presenti nel graph-II e viceversa. Quindi, la combinazione di entrambi i grafi dà un grafico completo di ‘n’ vertici.
Nota – Una combinazione di due grafi complementari dà un grafico completo.
Se ‘G’ è un qualsiasi grafico semplice, allora
|E(G)| + |E(‘G-‘)| = |E(Kn)|, dove n = numero di vertici nel grafico.
Esempio
Sia ‘G’ un grafo semplice con nove vertici e dodici bordi, trova il numero di bordi in ‘G-‘.
Si ha, |E(G)| + |E(‘G-‘)| = |E(Kn)|
12 &oltre; |E(‘G-‘)| =