Quando i dati sono pronti per essere analizzati, si dovrebbe valutare accuratamente, sulla base dell’ispezione dei dati, se i metodi statistici devono essere utilizzati per gestire i dati mancanti. Bell et al. hanno voluto valutare l’entità e la gestione dei dati mancanti negli studi clinici randomizzati pubblicati tra luglio e dicembre 2013 su BMJ, JAMA, Lancet e New England Journal of Medicine. Il 95% dei 77 studi identificati ha riportato alcuni dati di risultato mancanti. Il metodo più comunemente usato per gestire i dati mancanti nell’analisi primaria era l’analisi dei casi completa (45%), imputazione singola (27%), metodi basati su modelli (ad esempio, modelli misti o equazioni di stima generalizzate) (19%), e imputazione multipla (8%) .
Analisi dei casi completa
L’analisi dei casi completa è l’analisi statistica basata sui partecipanti con un set completo di dati di esito. I partecipanti con dati mancanti sono esclusi dall’analisi. Come descritto nell’introduzione, se i dati mancanti sono MCAR l’analisi dei casi completi avrà una potenza statistica ridotta a causa della ridotta dimensione del campione, ma i dati osservati non saranno distorti. Quando i dati mancanti non sono MCAR, la stima dell’analisi del caso completo potrebbe essere basata, cioè, ci sarà spesso un rischio di sovrastima del beneficio e di sottostima del danno. Si prega di consultare la sezione “Dovrebbe essere usata l’imputazione multipla per gestire i dati mancanti?” per una discussione più dettagliata della potenziale validità se viene applicata l’analisi completa dei casi.
Imputazione singola
Quando si usa l’imputazione singola, i valori mancanti sono sostituiti da un valore definito da una certa regola . Ci sono molte forme di imputazione singola, per esempio, l’ultima osservazione riportata (i valori mancanti di un partecipante sono sostituiti dall’ultimo valore osservato del partecipante), la peggiore osservazione riportata (i valori mancanti di un partecipante sono sostituiti dal peggiore valore osservato del partecipante), e l’imputazione media semplice. Nell’imputazione media semplice, i valori mancanti sono sostituiti dalla media per quella variabile. L’uso dell’imputazione singola spesso risulta in una sottostima della variabilità perché ogni valore non osservato ha lo stesso peso nell’analisi dei valori noti e osservati. La validità dell’imputazione singola non dipende dal fatto che i dati siano MCAR; l’imputazione singola dipende piuttosto da ipotesi specifiche che i valori mancanti, per esempio, siano identici all’ultimo valore osservato. Queste ipotesi sono spesso irrealistiche e l’imputazione singola è quindi spesso un metodo potenzialmente distorto e dovrebbe essere usato con grande cautela .
Imputazione multipla
L’imputazione multipla ha dimostrato di essere un metodo generale valido per gestire i dati mancanti negli studi clinici randomizzati, e questo metodo è disponibile per la maggior parte dei tipi di dati . Nelle sezioni seguenti descriveremo quando e come l’imputazione multipla dovrebbe essere usata.
L’imputazione multipla dovrebbe essere usata per gestire i dati mancanti?
Ragioni per cui l’imputazione multipla non dovrebbe essere usata per gestire i dati mancanti
È valido ignorare i dati mancanti?
L’analisi dei dati osservati (analisi dei casi completi) ignorando i dati mancanti è una soluzione valida in tre circostanze.
- a)
L’analisi dei casi completi può essere utilizzata come analisi primaria se le proporzioni di dati mancanti sono inferiori a circa il 5% (come regola generale) e non è plausibile che alcuni gruppi di pazienti (per esempio, i partecipanti molto malati o molto “bene”) siano specificamente persi al follow-up in uno dei gruppi confrontati. In altre parole, se l’impatto potenziale dei dati mancanti è trascurabile, allora i dati mancanti possono essere ignorati nell’analisi. In caso di dubbio si possono utilizzare le analisi di sensibilità del caso migliore e del caso peggiore: prima viene generato un set di dati dello scenario “caso migliore” in cui si presume che tutti i partecipanti persi al follow-up in un gruppo (indicato come gruppo 1) abbiano avuto un esito positivo (ad esempio, non hanno avuto un evento avverso grave); e tutti quelli con risultati mancanti nell’altro gruppo (gruppo 2) abbiano avuto un esito dannoso (ad esempio, hanno avuto un evento avverso grave). Quindi viene generato un set di dati dello scenario “worst-best-case” in cui si presume che tutti i partecipanti persi al follow-up nel gruppo 1 abbiano avuto un esito dannoso; e che tutti quelli persi al follow-up nel gruppo 2 abbiano avuto un esito benefico. Se vengono utilizzati risultati continui, allora un “risultato positivo” potrebbe essere la media del gruppo più 2 deviazioni standard (o 1 deviazione standard) della media del gruppo, e un “risultato dannoso” potrebbe essere la media del gruppo meno 2 deviazioni standard (o 1 deviazione standard) della media del gruppo. Per i dati dicotomizzati, queste analisi di sensibilità del caso migliore e peggiore mostreranno la gamma di incertezza dovuta ai dati mancanti, e se questa gamma non dà risultati qualitativamente contraddittori, allora i dati mancanti possono essere ignorati. Per i dati continui l’imputazione con 2 SD rappresenterà un possibile intervallo di incertezza dato il 95% dei dati osservati (se normalmente distribuiti).
- b)
Se solo la variabile dipendente ha valori mancanti e le variabili ausiliarie (variabili non incluse nell’analisi di regressione, ma correlate con una variabile con valori mancanti e/o legate alla sua mancanza) non sono identificate, l’analisi dei casi completi può essere utilizzata come analisi primaria e non si devono utilizzare metodi specifici per gestire i dati mancanti. Nessuna informazione aggiuntiva sarà ottenuta, per esempio, utilizzando l’imputazione multipla, ma gli errori standard possono aumentare a causa dell’incertezza introdotta dall’imputazione multipla.
- c)
Come menzionato sopra (vedi Metodi per gestire i dati mancanti), sarebbe anche valido semplicemente eseguire l’analisi dei casi completi se è relativamente certo che i dati sono MCAR (vedi Introduzione). È relativamente raro che sia certo che i dati siano MCAR. È possibile testare l’ipotesi che i dati siano MCAR con il test di Little, ma potrebbe essere poco saggio basarsi su test che si sono rivelati insignificanti. Quindi, se c’è un ragionevole dubbio che i dati siano MCAR, anche se il test di Little è insignificante (non riesce a rifiutare l’ipotesi nulla che i dati siano MCAR), allora MCAR non dovrebbe essere assunto.
Le proporzioni di dati mancanti sono troppo grandi?
Se mancano grandi proporzioni di dati dovrebbe essere considerato solo di riportare i risultati dell’analisi completa del caso e poi discutere chiaramente le limitazioni interpretative risultanti dei risultati dello studio. Se si usano imputazioni multiple o altri metodi per gestire i dati mancanti, si potrebbe indicare che i risultati dello studio sono confermativi, cosa che non sono se la mancanza è notevole. Se le proporzioni di dati mancanti sono molto grandi (per esempio, più del 40%) su variabili importanti, allora i risultati dello studio possono essere considerati solo come risultati che generano ipotesi. Una rara eccezione sarebbe se il meccanismo sottostante ai dati mancanti può essere descritto come MCAR (vedi paragrafo precedente).
L’ipotesi MCAR e l’ipotesi MAR sembrano entrambe implausibili?
Se l’ipotesi MAR sembra implausibile sulla base delle caratteristiche dei dati mancanti, allora i risultati della sperimentazione saranno a rischio di risultati distorti a causa di ‘incompletezza dei dati di esito’ e nessun metodo statistico può con certezza tenere conto di questo potenziale bias . La validità dei metodi utilizzati per gestire i dati MNAR richiede alcune ipotesi che non possono essere testate sulla base dei dati osservati. Le analisi di sensibilità dei casi migliori e peggiori possono mostrare l’intera gamma teorica di incertezza e le conclusioni dovrebbero essere correlate a questa gamma di incertezza. I limiti delle analisi dovrebbero essere discussi e considerati a fondo.
La variabile di risultato con valori mancanti è continua e il modello analitico è complicato (per esempio con interazioni)?
In questa situazione, si può considerare di usare il metodo della massima verosimiglianza diretta per evitare i problemi di compatibilità del modello tra il modello analitico e il modello di imputazione multipla, dove il primo è più generale del secondo. In generale, i metodi di massima verosimiglianza diretta possono essere usati, ma a nostra conoscenza i metodi disponibili in commercio sono attualmente disponibili solo per le variabili continue.
Quando e come usare le imputazioni multiple
Se nessuna delle ‘Ragioni per cui l’imputazione multipla non dovrebbe essere usata per gestire i dati mancanti’ di cui sopra è soddisfatta, allora l’imputazione multipla potrebbe essere usata. Varie procedure sono state suggerite in letteratura negli ultimi decenni per trattare i dati mancanti. Abbiamo delineato le suddette considerazioni sui metodi statistici per gestire i dati mancanti nella Fig. 1.
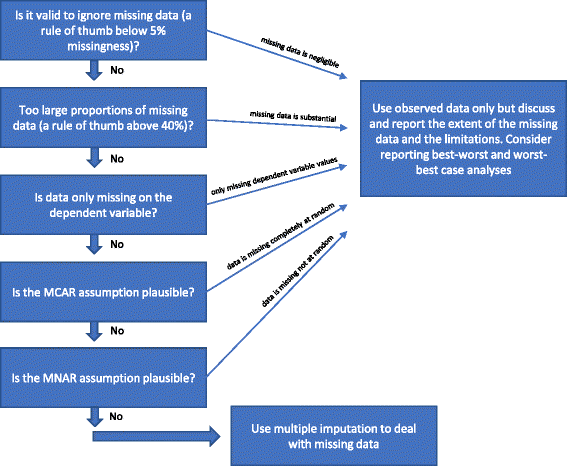
Flowchart: quando si dovrebbe usare l’imputazione multipla per gestire i dati mancanti nell’analisi dei risultati di studi clinici randomizzati
L’imputazione multipla è nata nei primi anni ’70, e ha guadagnato sempre più popolarità nel corso degli anni. L’imputazione multipla è una tecnica statistica basata sulla simulazione per la gestione dei dati mancanti. L’imputazione multipla consiste in tre fasi:
-
Fase di imputazione. Una ‘imputazione’ generalmente rappresenta un set di valori plausibili per i dati mancanti – l’imputazione multipla rappresenta più set di valori plausibili. Quando si usa l’imputazione multipla, i valori mancanti sono identificati e sostituiti da un campione casuale di imputazioni di valori plausibili (set di dati completati). I set di dati multipli completati sono generati attraverso un modello di imputazione scelto. Cinque set di dati imputati sono stati tradizionalmente suggeriti come sufficienti per motivi teorici, ma 50 set di dati (o più) sembrano preferibili per ridurre la variabilità di campionamento dal processo di imputazione. L’analisi desiderata viene eseguita separatamente per ogni set di dati che viene generato durante il passo di imputazione. In questo modo, per esempio, vengono costruiti 50 risultati di analisi.
-
Fase di pooling. I risultati ottenuti da ogni analisi di dati completati sono combinati in un unico risultato di imputazione multipla. Non c’è bisogno di condurre una meta-analisi ponderata in quanto tutti i risultati di 50 analisi sono considerati avere lo stesso peso statistico.
È di grande importanza che ci sia compatibilità tra il modello di imputazione e il modello di analisi o che il modello di imputazione sia più generale del modello di analisi (per esempio, che il modello di imputazione includa più covariate indipendenti del modello di analisi) . Per esempio, se il modello di analisi ha interazioni significative, allora il modello di imputazione dovrebbe includere anche queste, se il modello di analisi usa una versione trasformata di una variabile, allora il modello di imputazione dovrebbe usare la stessa trasformazione, ecc.
Diversi tipi di imputazione multipla
Diversi tipi di metodi di imputazione multipla esistono. Li presenteremo secondo il loro crescente grado di complessità: 1) analisi di regressione a valore singolo; 2) imputazione monotonica; 3) equazioni a catena o metodo Markov chain Monte Carlo (MCMC). Nei paragrafi seguenti descriveremo questi diversi metodi di imputazione multipla e come scegliere tra di essi.
Un’analisi di regressione a singola variabile include una variabile dipendente e le variabili di stratificazione utilizzate nella randomizzazione. Le variabili di stratificazione spesso includono un indicatore del centro se lo studio è uno studio multicentrico e di solito una o più variabili di aggiustamento con informazioni prognostiche che sono correlate all’esito. Quando si usa una variabile dipendente continua, può essere incluso anche un valore di base della variabile dipendente. Come menzionato in ‘Ragioni per cui i metodi statistici non dovrebbero essere usati per gestire i dati mancanti’, se solo la variabile dipendente ha valori mancanti e le variabili ausiliarie non sono identificate, dovrebbe essere eseguita un’analisi completa del caso e non dovrebbero essere usati metodi specifici per gestire i dati mancanti. Se le variabili ausiliarie sono state identificate, può essere eseguita un’imputazione a una sola variabile. Se ci sono mancanze significative sulla variabile di base di una variabile continua, un’analisi completa dei casi può fornire risultati distorti. Pertanto, in tutti i casi, un’imputazione a singola variabile (con o senza variabili ausiliarie incluse a seconda dei casi) viene condotta se solo la variabile di base è mancante.
Se sia la variabile dipendente che la variabile di base sono mancanti e la mancanza è monotona, viene effettuata un’imputazione monotona. Supponiamo una matrice di dati in cui i pazienti sono rappresentati da righe e le variabili da colonne. La missingness di tale matrice di dati è detta monotona se le sue colonne possono essere riordinate in modo tale che per ogni paziente (a) se un valore è mancante tutti i valori a destra della sua posizione sono anche mancanti, e (b) se un valore è osservato tutti i valori a sinistra di questo valore sono anche osservati. Se la mancanza è monotona, il metodo di imputazione multipla è anche relativamente semplice, anche se più di una variabile ha valori mancanti. In questo caso è relativamente semplice imputare i dati mancanti usando l’imputazione di regressione sequenziale dove i valori mancanti sono imputati per ogni variabile alla volta. Molti pacchetti statistici (per esempio, STATA) possono analizzare se la mancanza è monotona o no.
Se la mancanza non è monotona, viene condotta un’imputazione multipla utilizzando le equazioni concatenate o il metodo MCMC. Le variabili ausiliarie sono incluse nel modello se sono disponibili. Abbiamo riassunto come scegliere tra i diversi metodi di imputazione multipla nella Fig. 2.
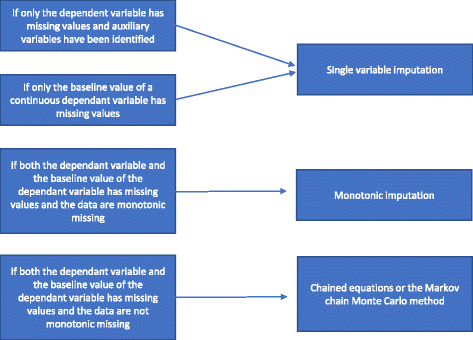
Flowchart of multiple imputation
Full information maximum likelihood
Full information maximum likelihood è un metodo alternativo per trattare i dati mancanti. Il principio della stima della massima verosimiglianza è quello di stimare i parametri della distribuzione congiunta dell’esito (Y) e delle covariate (X1,…, Xk) che, se fossero veri, massimizzerebbero la probabilità di osservare i valori che in effetti abbiamo osservato. Se i valori sono mancanti in un dato paziente, possiamo ottenere la probabilità sommando la solita probabilità su tutti i possibili valori dei dati mancanti, purché il meccanismo dei dati mancanti sia ignorabile. Questo metodo è chiamato massima verosimiglianza a piena informazione.
La massima verosimiglianza a piena informazione ha sia punti di forza che limitazioni rispetto all’imputazione multipla.
Punti di forza della massima verosimiglianza a piena informazione rispetto all’imputazione multipla
- 1)
È più semplice da implementare, cioè non è necessario passare attraverso diversi passaggi come quando si usa l’imputazione multipla.
- 2)
A differenza dell’imputazione multipla, la massima verosimiglianza a piena informazione non ha potenziali problemi di incompatibilità tra il modello di imputazione e quello di analisi (vedi ‘Imputazione multipla’). La validità dei risultati di imputazione multipla sarà discutibile se c’è un’incompatibilità tra il modello di imputazione e il modello di analisi, o se il modello di imputazione è meno generale del modello di analisi.
- 3)
Quando si usa l’imputazione multipla, tutti i valori mancanti in ogni set di dati generato (fase di imputazione) sono sostituiti da un campione casuale di valori plausibili. Quindi, a meno che non venga specificato “un seme casuale”, ogni volta che viene eseguita un’analisi di imputazione multipla verranno mostrati risultati diversi. Le analisi quando si utilizza la massima verosimiglianza di informazioni complete sullo stesso set di dati produrranno gli stessi risultati ogni volta che l’analisi viene eseguita, e i risultati non dipendono quindi da un seme di numeri casuali. Tuttavia, se il valore del seme casuale è definito nel piano di analisi statistica, questo problema può essere risolto.
Limitazioni della massima verosimiglianza a piena informazione rispetto all’imputazione multipla
Le limitazioni dell’uso della massima verosimiglianza a piena informazione rispetto all’uso dell’imputazione multipla, è che l’uso della massima verosimiglianza a piena informazione è possibile solo utilizzando un software appositamente progettato. Sono stati sviluppati software preliminari progettati, ma la maggior parte di questi manca delle caratteristiche dei software statistici progettati commercialmente (per esempio, STATA, SAS o SPSS). In STATA (utilizzando il comando SEM) e SAS (utilizzando il comando PROC CALIS), è possibile utilizzare la massima verosimiglianza a piena informazione, ma solo quando si utilizzano variabili dipendenti continue (outcome). Per la regressione logistica e la regressione di Cox, l’unico pacchetto commerciale che fornisce la massima verosimiglianza a piena informazione per i dati mancanti è Mplus.
Un ulteriore limite potenziale quando si usa la massima verosimiglianza a piena informazione è che ci può essere un presupposto sottostante di normalità multivariata. Tuttavia, le violazioni dell’ipotesi di normalità multivariata potrebbero non essere così importanti, quindi potrebbe essere accettabile includere variabili indipendenti binarie nell’analisi.
Abbiamo incluso nel file aggiuntivo 1 un programma (SAS) che produce un set di dati full toy che include diverse analisi di questi dati. La tabella 1 e la tabella 2 mostrano l’output e come i diversi metodi che gestiscono i dati mancanti producono risultati diversi.
Analisi di regressione dei valori del panel
I dati del panel sono solitamente contenuti in un cosiddetto file di dati ampio in cui la prima riga contiene i nomi delle variabili e le righe successive (una per ogni paziente) contengono i valori corrispondenti. L’esito è rappresentato da diverse variabili – una per ogni misurazione pianificata e temporizzata dell’esito. Per analizzare i dati, si deve convertire il file in un cosiddetto long file con un record per ogni misurazione pianificata dell’esito, includendo il valore dell’esito, il tempo della misurazione e una copia di tutti gli altri valori delle variabili esclusi quelli della variabile dell’esito. Per mantenere le correlazioni all’interno del paziente tra le misurazioni di esito cronometrate, è pratica comune eseguire un’imputazione multipla del file di dati nella sua forma ampia seguita da un’analisi del file risultante dopo che è stato convertito nella sua forma lunga. Proc mixed (SAS 9.4) può essere utilizzato per l’analisi di valori di risultato continui e proc. glimmix (SAS 9.4) per altri tipi di risultato. Poiché queste procedure applicano il metodo della massima verosimiglianza diretta sui dati di risultato, ma ignorano i casi con valori di covariate mancanti, le procedure possono essere utilizzate direttamente quando mancano solo i valori della variabile dipendente e non sono disponibili buone variabili ausiliarie. Altrimenti, la proc. mixed o la proc. glimmix (a seconda del caso) dovrebbe essere usata dopo un’imputazione multipla. Chiaramente, un approccio corrispondente può essere possibile usando altri pacchetti statistici.
Analisi di sensibilità
Le analisi di sensibilità possono essere definite come un insieme di analisi in cui i dati sono trattati in modo diverso rispetto all’analisi primaria. Le analisi di sensibilità possono mostrare come le ipotesi, diverse da quelle fatte nell’analisi primaria, influenzano i risultati ottenuti. L’analisi di sensibilità dovrebbe essere predefinita e descritta nel piano di analisi statistica, ma ulteriori analisi di sensibilità post hoc potrebbero essere giustificate e valide. Quando la potenziale influenza dei valori mancanti non è chiara, raccomandiamo le seguenti analisi di sensibilità:
-
Abbiamo già descritto l’uso delle analisi di sensibilità best-worst e worst-best case per mostrare la gamma di incertezza dovuta ai dati mancanti (vedi Valutazione dell’opportunità di utilizzare metodi per gestire i dati mancanti). La nostra precedente descrizione delle analisi di sensibilità del caso migliore e peggiore si riferiva a dati mancanti su una variabile dipendente dicotomica o continua, ma queste analisi di sensibilità possono essere utilizzate anche quando mancano dati su variabili di stratificazione, valori di base, ecc. La potenziale influenza dei dati mancanti dovrebbe essere valutata per ogni variabile separatamente, cioè, ci dovrebbe essere uno scenario migliore e uno peggiore per ogni variabile (variabile dipendente, l’indicatore di risultato e le variabili di stratificazione) con dati mancanti.
-
Se si decide che, per esempio, si devono usare imputazioni multiple, allora questi risultati dovrebbero essere il risultato primario del risultato dato. Ogni analisi di regressione primaria dovrebbe sempre essere integrata da una corrispondente analisi dei casi osservati (o disponibili).
Quando si utilizzano metodi a effetti misti
L’utilizzo di un disegno di studio multicentrico sarà spesso necessario per reclutare un numero sufficiente di partecipanti allo studio entro un periodo di tempo ragionevole. Un disegno di studio multicentrico fornisce anche una base migliore per la successiva generalizzazione dei risultati. E’ stato dimostrato che i metodi di analisi più comunemente usati negli studi clinici randomizzati funzionano bene con un piccolo numero di centri (analizzando gli esiti binari dipendenti). Con un numero relativamente grande di centri (50 o più), è spesso ottimale utilizzare il “centro” come effetto casuale e utilizzare metodi di analisi ad effetto misto. Sarà spesso valido anche utilizzare metodi di analisi a effetti misti quando si analizzano dati longitudinali . In alcune circostanze potrebbe essere valido includere la covariata “effetto casuale” (per esempio “centro”) come covariata a effetto fisso durante la fase di imputazione e quindi utilizzare l’analisi del modello misto o le equazioni di stima generalizzate (GEE) durante la fase di analisi. Tuttavia, l’applicazione di un modello a effetti misti (con, per esempio, “centro” come effetto casuale) implica che la struttura a più livelli dei dati deve essere presa in considerazione durante la modellizzazione dell’imputazione multipla. Ora, il software commerciale non è direttamente disponibile per farlo. Tuttavia, si può usare il pacchetto REALCOME che può essere interfacciato con STATA. L’interfaccia esporta i dati con valori mancanti da STATA a REALCOM dove l’imputazione viene fatta tenendo conto della natura multilivello dei dati e utilizzando un metodo MCMC che include le variabili continue e utilizzando un modello normale latente permette anche una corretta gestione dei dati discreti. I set di dati imputati possono quindi essere analizzati utilizzando il comando STATA ‘mi estimate:’ che può essere combinato con l’istruzione ‘mixed’ (per un risultato continuo) o l’istruzione ‘meqrlogit’ per risultati binari o ordinali in STATA. Nell’analisi dei dati panel, tuttavia, ci si può facilmente trovare di fronte a una situazione in cui i dati includono tre o più livelli, per esempio, misure all’interno dello stesso paziente (livello-1), pazienti all’interno di centri (livello-2), e centri (livello-3). Per non essere coinvolti in un modello piuttosto complicato che può portare alla mancanza di convergenza o a errori standard instabili e per il quale non è disponibile un software commerciale, si consiglia di trattare l’effetto centro come fisso (direttamente o in seguito alla fusione di piccoli centri in uno o più centri di dimensioni adeguate, utilizzando una procedura che deve essere prescritta nel piano di analisi statistica) o escludere il centro come covariata. Se la randomizzazione è stata stratificata per centro, quest’ultimo approccio porterà ad una distorsione verso l’alto degli errori standard con conseguente procedura di test un po’ conservativa .
.