Introductory Business Statistics

Considerate la seguente serie di dati.
4; 5; 6; 6; 6; 6; 7; 7; 7; 7; 7; 7; 8; 8; 8; 9; 10

Questa serie di dati può essere rappresentata dal seguente istogramma. Ogni intervallo ha larghezza uno, e ogni valore si trova nel mezzo di un intervallo.

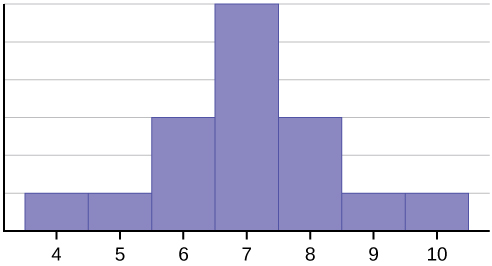
L’istogramma mostra una distribuzione simmetrica dei dati. Una distribuzione è simmetrica se una linea verticale può essere tracciata in qualche punto dell’istogramma in modo tale che la forma a sinistra e a destra della linea verticale siano immagini speculari l’una dell’altra. La media, la mediana e la modalità sono sette per questi dati. In una distribuzione perfettamente simmetrica, la media e la mediana sono uguali. Questo esempio ha una modalità (unimodale), e la modalità è la stessa della media e della mediana. In una distribuzione simmetrica che ha due modalità (bimodale), le due modalità sarebbero diverse dalla media e dalla mediana.

L’istogramma per i dati: 4566677778 non è simmetrico. Il lato destro sembra “tagliato” rispetto al lato sinistro. Una distribuzione di questo tipo si chiama inclinata a sinistra perché è tirata verso sinistra. Possiamo misurare formalmente l’asimmetria di una distribuzione così come possiamo misurare matematicamente il peso centrale dei dati o la sua “speadness” generale. La formula matematica per l’asimmetria è: . Maggiore è la deviazione da zero, maggiore è il grado di asimmetria. Se l’asimmetria è negativa, allora la distribuzione è inclinata a sinistra come in (Figura). Una misura positiva dell’asimmetria indica un’asimmetria a destra come in (Figura).

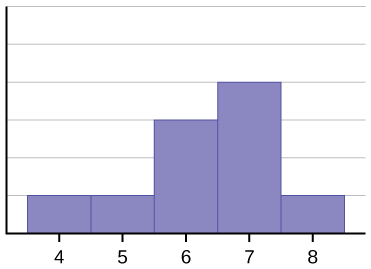
La media è 6,3, la mediana è 6,5, e la modalità è sette. Notate che la media è inferiore alla mediana, ed entrambe sono inferiori alla modalità. La media e la mediana riflettono entrambe l’inclinazione, ma la media la riflette di più.

L’istogramma per i dati: 67777888910, non è simmetrico. È inclinato a destra.

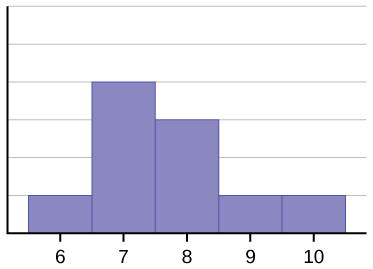
La media è 7,7, la mediana è 7,5 e la modalità è sette. Delle tre statistiche, la media è la più grande, mentre la modalità è la più piccola. Di nuovo, la media riflette la distorsione più grande.

Per riassumere, generalmente se la distribuzione dei dati è distorta a sinistra, la media è inferiore alla mediana, che spesso è inferiore alla modalità. Se la distribuzione dei dati è inclinata a destra, la modalità è spesso inferiore alla mediana, che è inferiore alla media.

Come per la media, la mediana e la modalità, e come vedremo tra poco, la varianza, esistono formule matematiche che ci danno misure precise di queste caratteristiche della distribuzione dei dati. Sempre guardando la formula dell’asimmetria vediamo che questa è una relazione tra la media dei dati e le singole osservazioni al cubo.

dove è la deviazione standard del campione dei dati, , e è la media aritmetica e è la dimensione del campione.

Formalmente la media aritmetica è conosciuta come il primo momento della distribuzione. Il secondo momento che vedremo è la varianza, e l’asimmetria è il terzo momento. La varianza misura le differenze al quadrato dei dati dalla media e l’asimmetria misura le differenze al cubo dei dati dalla media. Mentre la varianza non può mai essere un numero negativo, la misura dell’asimmetria può, ed è così che si determina se i dati sono inclinati a destra o a sinistra. L’asimmetria per una distribuzione normale è zero, e qualsiasi dato simmetrico dovrebbe avere un’asimmetria vicina allo zero. Valori negativi per l’asimmetria indicano dati che sono sbilanciati a sinistra e valori positivi per l’asimmetria indicano dati che sono sbilanciati a destra. Con l’asimmetria a sinistra, intendiamo che la coda sinistra è lunga rispetto alla coda destra. Allo stesso modo, skewed right significa che la coda destra è lunga rispetto alla coda sinistra. L’asimmetria caratterizza il grado di asimmetria di una distribuzione intorno alla sua media. Mentre la media e la deviazione standard sono quantità dimensionali (ecco perché prenderemo la radice quadrata della varianza), cioè hanno le stesse unità delle quantità misurate , l’asimmetria è convenzionalmente definita in modo tale da renderla non dimensionale. È un numero puro che caratterizza solo la forma della distribuzione. Un valore positivo di skewness indica una distribuzione con una coda asimmetrica che si estende verso X più positivo e un valore negativo indica una distribuzione la cui coda si estende verso X più negativo. Una misura zero di skewness indicherà una distribuzione simmetrica.

Skewness e simmetria diventano importanti quando si parla di distribuzioni di probabilità nei capitoli successivi.