Proprio come la torta si possono avere 2 pezzi piccoli o 1 pezzo grande il doppio ed è la stessa quantità. Quindi molte frazioni sono equivalenti, come 2/5 e 4/10.


Qualsiasi numero può essere scritto come una frazione
Scrivi qualsiasi numero intero superiore a 1 per renderlo una frazione poiché il numero totale di parti in qualsiasi intero indiviso è uno.
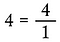
Moltiplicare frazioni in senso trasversale
Moltiplicare frazioni è facile, basta moltiplicare in senso trasversale.
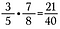
Nota: I numeri misti devono essere trasformati prima in frazioni improprie, continua a leggere per saperne di più.
Moltiplicare per qualsiasi forma di uno in qualsiasi momento
Il numero 1 è chiamato identità moltiplicativa perché possiamo moltiplicarlo per qualsiasi numero e il numero rimane lo stesso. Questo è importante per le frazioni perché spesso abbiamo bisogno di alterare l’aspetto di una frazione senza effettivamente cambiare il suo valore.
Per esempio, posso cambiare 1/3 nella frazione equivalente 3/9 moltiplicando per 3/3.
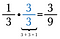
Aggiungi e sottrai parti uguali
Quando si aggiungono e sottraggono frazioni i denominatori devono essere uguali. Questo ha senso. Se vogliamo unire o togliere parti dobbiamo parlare di parti delle stesse dimensioni, altrimenti si farebbe confusione.
Quindi cosa fai se le tue frazioni non hanno le stesse dimensioni?
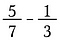
Moltiplicare per una forma di uno per cambiare i denominatori in una dimensione comune. Essenzialmente, stiamo dividendo le frazioni in pezzi più piccoli fino a quando non sono della stessa dimensione. Questo si chiama trovare un denominatore comune.
In verità, qualsiasi denominatore comune va bene, ma la gente preferisce trovare il più piccolo. In questo caso il più piccolo numero in cui 7 e 3 entrano senza resto è 21. Quindi moltiplicate la prima frazione per 3/3 e la seconda per 7/7.
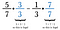
Se non potete pensare al minimo denominatore comune, potete sempre moltiplicare ogni frazione per la denominazione opposta. A volte, come in questo caso, questo risulta essere il minimo comune denominatore. Se non lo è, basta ridurre la risposta alla fine.
Una volta che i denominatori corrispondono, sottrarre i numeratori per ottenere 8/21.
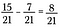
Questo funziona come ci si aspetta. Pittoricamente, cominciamo con 15 pezzi di 21 totali.

Rimuovere la colorazione da 7 dei 15 blocchi blu.

Che lascia 8/21 come previsto.
Cambia prima i numeri misti
Un numero misto è la combinazione di un numero intero e una frazione.
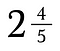
I numeri misti non giocano bene con altre frazioni. È una buona idea convertirli prima in frazioni improprie.
Nota: Una frazione impropria è una frazione il cui numeratore è più grande del suo denominatore e quindi ha un valore maggiore di uno.
Convertire un numero misto è davvero un’addizione
Per convertire 2 e 4/5 in una frazione impropria aggiungere 2 + 4/5.
Passo 1: Iniziare riscrivendo 2 come 2/1.
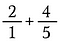
Passo 2: Moltiplicare 2/1 per 5/5 per fare una frazione equivalente di 10/5 che ha il denominatore comune desiderato di 5.
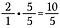
Passo 3: Aggiungere 10/5 + 4/5.
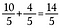
Il nostro risultato è la frazione impropria equivalente 14/5.
Per convertire nuovamente in un numero misto eseguire la divisione. Per esempio, 5 va in 14 due volte (poiché 5 x 2 = 10) con 4 pezzi rimasti.
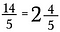
Confrontare frazioni usando il prodotto incrociato
Supponiamo di voler determinare quale sia più grande: 5/12 o 6/13.
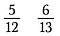
Passo uno: Moltiplicare una diagonale e scrivere il prodotto sopra il numeratore.
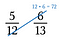
Fase due: Moltiplicare l’altra diagonale e scrivere il suo prodotto sopra il numeratore.
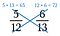
Passo tre: Confrontare i prodotti. Il lato con il prodotto più grande è la frazione più grande. Quindi in questo caso, 5/12 è meno di 6/13.
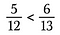
Possiamo determinare se le frazioni sono uguali usando anche i prodotti incrociati.
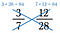
Il prodotto incrociato di 3/7 e 12/28 sono entrambi 84, quindi 3/7 = 12/28.
Annulla qualsiasi cosa che divide per uno
La cosa migliore delle frazioni è che puoi trovare molte opportunità di annullare. Il che le rende veloci e facili da gestire.
Supponiamo che io abbia la frazione 8/10. Sia 8 che 10 possono essere riscritti con 2 come fattore.
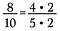
Perché 2/2 = 1, posso cancellare i 2 lasciando 4/5 come frazione ridotta.
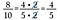
Utilizzare questa strategia per rendere più facile anche la moltiplicazione delle frazioni.
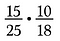
Inizia riscrivendo ogni numero in fattori.
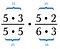
Cancella ogni coppia di numeri che divide per 1. Per esempio, 5/5 = 1.
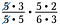
Ho anche un’altra coppia di 5 e una coppia di 3 che dividono per 1.
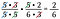
Ops! Avrei potuto riscrivere 6 come 2 x 3 e cancellare una coppia di 2. Va bene se si perde un fattore, basta continuare finché non li si ottiene tutti.
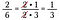
Ha moltiplicato 15/25 per 10/18 direttamente sarebbe stata un sacco di aritmetica, usando l’annullamento ho pre-ridotto le frazioni e reso più semplice la moltiplicazione.
Utilizzare la moltiplicazione per dividere le frazioni
Il concetto di dividere le frazioni è facile con semplici esempi come:

Ci sono due metà in un intero, quindi ci sono 10 metà in 5 interi.
Ma il concetto diventa difficile con frazioni più complicate.
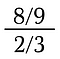
Per risolvere questo problema utilizzeremo due fatti:
- Possiamo moltiplicare per qualsiasi forma di uno (cioè qualsiasi cosa sopra se stessa).Cioè qualsiasi cosa sopra se stessa)
- Moltiplicando per il reciproco di 3/2, che è 2/3, si ottiene 1 tramite l’annullamento
Passo uno: Iniziare moltiplicando per il reciproco su se stesso.
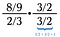
Ora abbiamo due piccoli problemi da risolvere (blu e verde).
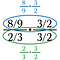
Fase due: Annullare tutto ciò che divide per 1 nella frazione inferiore (verde). Questo dovrebbe sempre dare come risultato 1.

Ora ci rimane il problema superiore da risolvere.
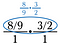
Fase tre: Usa l’annullamento per pre-ridurre la frazione. Dopo aver fatto queste riduzioni, moltiplicare attraverso per ottenere 4/3.

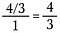
Scorciatoia
Questa è la meccanica della mano lunga di “capovolgere e moltiplicare.”
Possiamo saltare la moltiplicazione per il reciproco in basso poiché si annulla sempre a 1. Quindi tutto quello che devi fare è moltiplicare il numeratore per il reciproco del denominatore.

Bonus: Teoria, nel caso tu sia interessato…
Grande domanda! Per generalizzare, fai due frazioni usando le lettere a, b, c e d per rappresentare quattro numeri diversi.
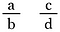
Moltiplicare entrambe le frazioni per b-d (questo ci permetterà di annullare i denominatori).
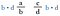
Ora annulliamo le b a sinistra e le d a destra poiché si dividono per 1. Non abbiamo più frazioni, solo i prodotti d-a e c-b.
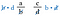
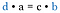
Riguarda le frazioni originali. Questi sono gli stessi prodotti come se avessimo moltiplicato le diagonali. Pertanto, la scorciatoia è confrontare il prodotto incrociato.
❤ RIMANI COLLEGATO ❤
Rimani aggiornato con tutto ciò che Math Hacks sta facendo!