Le equazioni Lotka-Volterra descrivono un modello ecologico predatore-preda (o parassita-ospite) che assume che, per un insieme di costanti positive fisse 
(il tasso di crescita delle prede), 
(il tasso al quale i predatori distruggono le prede), 
(il tasso di morte dei predatori), e 
(il tasso al quale i predatori aumentano consumando le prede), valgono le seguenti condizioni
1. Una popolazione di prede 
aumenta ad un tasso 
(proporzionale al numero di prede) ma è contemporaneamente distrutta dai predatori ad un tasso 
(proporzionale al prodotto del numero di prede e predatori).
2. Una popolazione di predatori 
diminuisce ad un tasso 
(proporzionale al numero di predatori), ma aumenta ad un tasso 
(di nuovo proporzionale al prodotto del numero di prede e predatori).
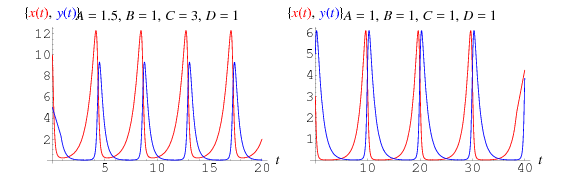
Questo dà le equazioni differenziali accoppiate
 |
 |
 |
(1)
|
 |
 |
 |
(2)
|
le cui soluzioni sono riportate sopra, dove le prede sono mostrate in rosso e i predatori in blu. In questo tipo di modello, la curva delle prede conduce sempre la curva dei predatori.
I punti critici si verificano quando 
, quindi
 |
 |
 |
(3)
|
 |
 |
 |
(4)
|
L’unico punto fermo si trova quindi a 
.