Introduzione
Questa pagina esamina l’equazione di continuità, che impone la conservazione della massa in un’analisi euleriana. Questa non è strettamente una descrizione del comportamento dei materiali, ma l’equazione risultante è spesso usata come identità per manipolare algebricamente i modelli costitutivi che descrivono il comportamento dei materiali. Quindi vale la pena rivederla. È anche centrale per l’analisi del flusso dei fluidi perché le analisi classiche dei fluidi non possono essere lagrangiane poiché le posizioni di tutte le particelle del fluido a \(t = 0\) sono sconosciute.
Conservazione della massa
L’equazione di continuità riflette il fatto che la massa è conservata in qualsiasi analisi di meccanica del continuo non nucleare. L’equazione è sviluppata sommando il tasso al quale la massa fluisce dentro e fuori un volume di controllo, e impostando il flusso netto in entrata uguale al tasso di cambiamento della massa all’interno di esso. Questo è dimostrato nella figura sottostante.
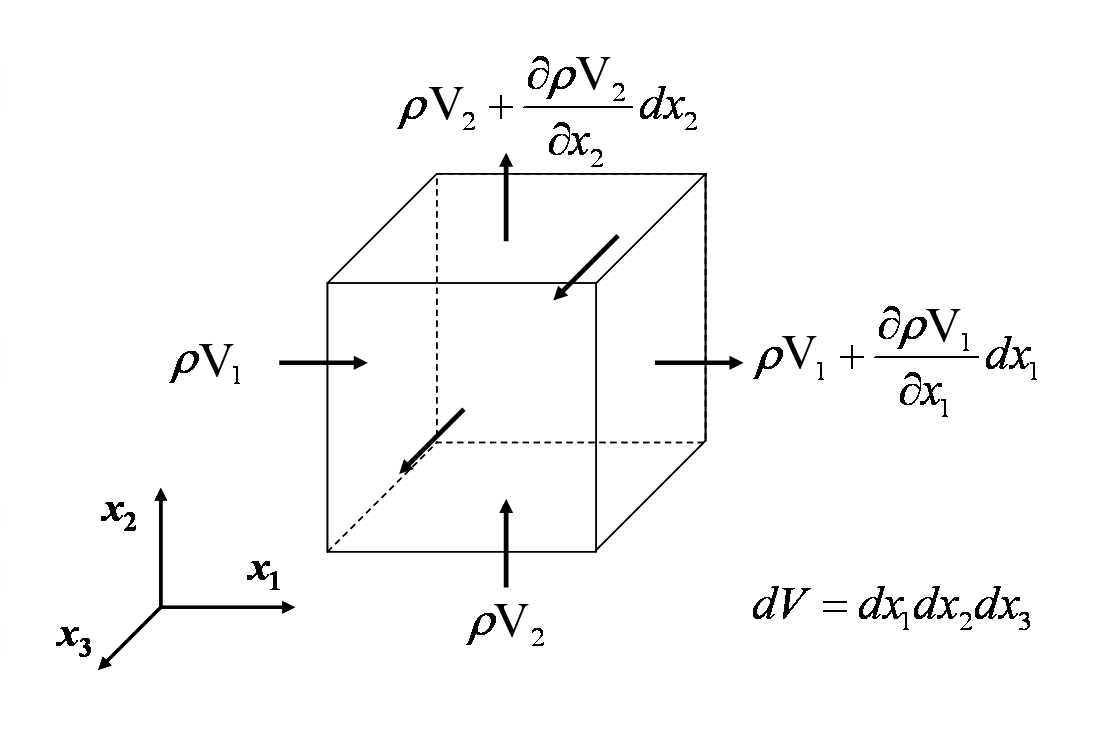
Equagliando tutte le portate di massa in entrata e in uscita dal volume di controllo differenziale si ottiene
Cancellando i termini e dividendo per \(dx_1 dx_2 dx_3\) si ottiene
\
e riordinando si ottiene
Questo può essere scritto concisamente come
\

Punti importanti
Queste sono le forme finali, Queste sono le forme finali, complete e più generali della equazione di continuità che applica la conservazione della massa. Si applica a tutti i materiali, non solo ai fluidi. Quindi si applica anche ai solidi. Si noti che è una singola equazione scalare ed è di natura euleriana perché i gradienti sono \(\parziale \su \parziale x_i}\), non \(\parziale \su \parziale X_i}).
Si potrebbe chiedere se c’è una controparte lagrangiana alla forma euleriana di questa. C’è. Di solito si scrive come
Questo afferma semplicemente che il tronco differenziale della massa nello stato deformato (\rho \, dV\) deve essere uguale al suo valore originale (\rho_o dV_o\) nello stato indeformato.
Ci sono diversi casi speciali dell’equazione di continuità.Il primo si verifica quando il flusso è allo stato stazionario. In questo caso, la derivata rispetto al tempo è zero, lasciando.
Il secondo caso speciale è quello dell’incomprimibilità, cioè, \In questo caso la derivata rispetto al tempo è zero e \(\rho\) può essere eliminato dall’equazione lasciando solo
Questo risultato è abbastanza semplice che viene spesso espanso.
Nota che questo non è altro che \(\testo{tr}({\bf D}) = 0\) per il caso di materiali incomprimibili.

Derivata del materiale
Il seguente è degno di nota perché permette di separare il vettore densità e velocità. Il primo passo è applicare la regola del prodotto al termine di divergenza nell’equazione di continuità.
E poi si noti che \(\parziale \rho \su \parziale t} + {\bf v} \cdot \nabla \rho\)è solo la derivata materiale della densità,\({D \rho \su D t}).
Quindi l’equazione di continuità può anche essere scritta come
\7556>Se il materiale è incomprimibile, allora \(\rho\) non può cambiare, quindi \(D \rho\su D t}) deve essere zero, lasciando
\
E poi dividere per \(\rho\) (dato che non è zero) per ottenere
\

Esempio di equazione di continuità
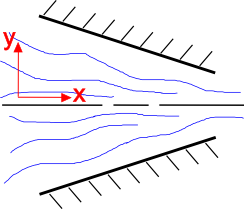
È intuitivo che il flusso del fluido accelera al diminuire della sezione trasversale, come mostrato a destra. L’equazione di continuità spiega questo. Consideriamo un campo di flusso 2-D, in stato stazionario, di un fluido incomprimibile. L’equazione di continuità per questa situazione è
Partiamo guardando la componente y del flusso, \(v_2\). La geometria dell’ugello convergente costringe la componente \(v_2\) a fluire verso l’alto quando \(y \lt 0\) e verso il basso quando \(y \gt 0\). Così \(v_2 \segue 0\) quando \ y \segue 0\) e \(v_2 \segue 0\) quando \(y \segue 0\).
L’effetto netto di questo è che \(v_2 parziale su \x_2 parziale} \l’0)nell’ugello convergente.
Ma l’equazione di continuità impone che la somma delle due derivate parziali deve essere uguale a zero. Quindi, se la seconda è minore di zero, allora
e questo significa che il flusso del fluido deve essere in accelerazione.