Concavo e convesso?

Qual è la differenza tra concavo e convesso?

Se dovessimo descrivere la differenza tra concavo e convesso nel modo più generale possibile, diremmo che qualsiasi oggetto cavo, simile a una ciotola, è concavo, mentre qualsiasi oggetto simile a una palla da rugby o da calcio ha una forma convessa. Ma forse la ragione per cui convesso e concavo sono così comunemente usati in modo errato è che le due parole non sono così semplici come vorremmo che fossero.

La maggior parte delle fonti grammaticali insistono su come sia possibile utilizzare la mnemotecnica per decifrare convesso e concavo attraverso la parola caverna. Mentre la nozione di associare concavo all’evento di qualcosa che “spacca” aiuta a imparare le caratteristiche della superficie, è confuso mettere in relazione questa idea con soggetti che coinvolgono i grafici.

Per capire come concavo e convesso sono diversi l’uno dall’altro, abbiamo bisogno di imparare come ogni termine è usato nella capacità della matematica, degli specchi, delle lenti, e, infine, all’interno della scrittura creativa. Una volta che avete deciso in quale contesto vorreste usare parole come concavo e convesso, imparare i loro aspetti tecnici vi permetterà di essere più sicuri nell’usarle nel discorso quotidiano.

Cosa significa concavo?

Concavo è usato come aggettivo o sostantivo per descrivere la forma di un oggetto o di una superficie che è curva verso l’interno o incavata come una ciotola. Esempi di concavo in una frase includono,

“Ha raccolto il gelato dal contenitore, lasciando un’impronta concava.”

Secondo l’Oxford Dictionary of Word Histories, la parola concava deriva dal tardo inglese medio. Concavo e concavità rendono il termine latino concavus (con- e cavus), che si traduce in ‘insieme’ e ‘cavo’ (“Concave,” 110).

I sinonimi di concavo includono:

Dentellato, depresso, dished, cavo, dentellato, incassato e affondato.

Antonimi di concavo includono:

Bulging, cambered, sporgente, sporgente, protuberante.

Cosa significa convesso?

La parola convesso, o convessità, è un aggettivo che descrive un oggetto o una superficie che è arrotondata o curva. Per quanto riguarda gli oggetti, la superficie centrale di un oggetto convesso è più larga del suo angolo esterno. Esempi di convessità in una frase includono,

“Sono caduto nell’edera velenosa e ora ho bolle rosse e convesse su tutta la pelle”.

I sinonimi di convesso includono:

Arcato, piegato, rigonfio, sollevato.

Antonimi di convesso includono:

Depresso, sprofondato.

Funzioni concave vs convesse

Una funzione convessa rappresenta una linea continua su un grafico dove il punto medio, o mediano intero di un dominio, non supera la media dell’intervallo. Una funzione concava è l’esatto opposto di una funzione convessa perché, perché f(x) sia concava, f(x) deve essere negativa. Per rendere le differenze più chiare, ecco un rapido riepilogo di come i termini si confrontano:

Concava verso l’alto = convessa = convessa verso il basso

Concava verso il basso = concava = convessa verso l’alto

La differenza tra funzioni concave e convesse si mostra più chiaramente se guardiamo un grafico. Notate come la funzione convessa si apre verso l’alto, mentre la funzione concava si apre verso il basso.

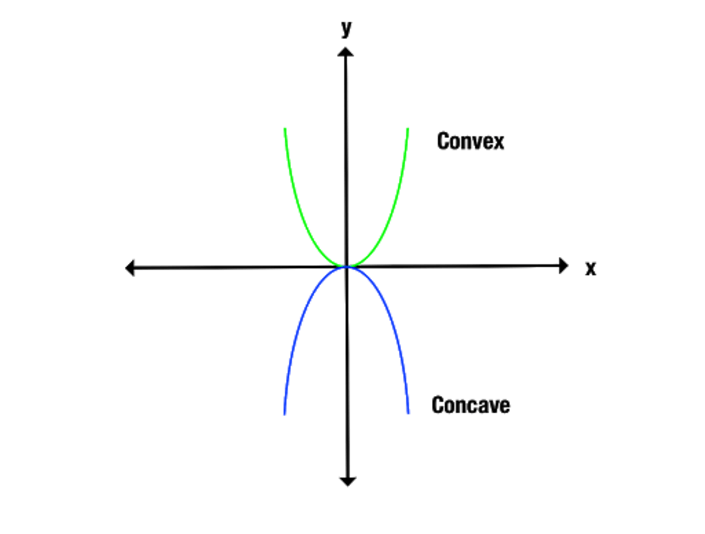
Un altro modo di identificare le funzioni concave e convesse è collegare i punti sul grafico lungo l’asse delle x. Una funzione concava collega solo linee sotto il grafico, mentre una funzione convessa produce solo linee sopra il grafico.

Possiamo inoltre usare il calcolo per decifrare se una funzione è convessa o concava. Se la derivata seconda di f(x) è maggiore di zero, allora la funzione è convessa. Ma se la derivata seconda di f(x) è minore di zero, la funzione è concava.

Poligoni convessi e concavi

Non spaventatevi, ma le parole convesso e concavo sono usate anche in geometria. Le forme convesse e concave sono più spesso discusse in riferimento ai poligoni, che sono forme con un minimo di tre lati e angoli.

Esistono poligoni regolari con lati e angoli uguali, ma i poligoni convessi e concavi sono un po’ più complicati. I poligoni convessi contengono angoli interni che sono minori di 180 gradi, mentre i poligoni concavi contengono uno o più angoli interni che sono maggiori di 180 gradi.

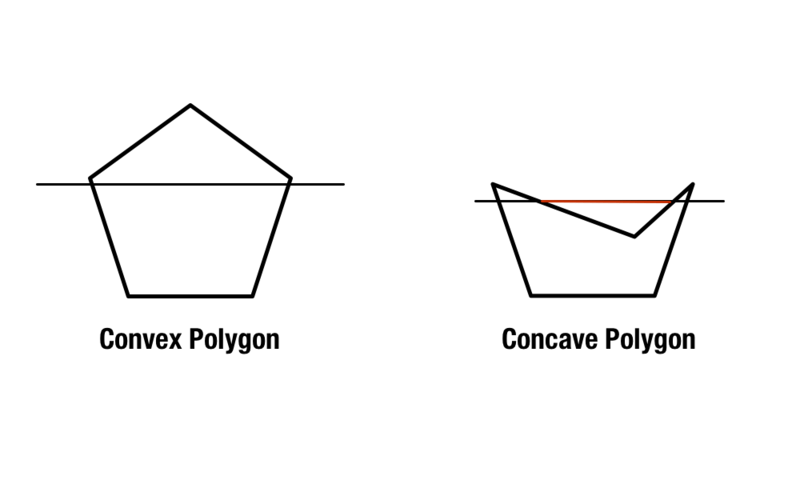
Un secondo metodo per identificare i poligoni concavi e convessi è quello di tracciare due linee diagonali attraverso la forma, partendo dagli angoli della forma. Se ogni linea esiste all’interno della forma, la forma è convessa. Se c’è almeno una linea che attraversa al di fuori della forma, è concava.

Specchi concavi e convessi

Le parole concavo e convesso sono comunemente usate quando si parla di oggetti ottici, come specchi e lenti. Qualsiasi superficie convessa sporgerà verso l’esterno, simile a una bolla, che dà l’effetto di ampiezza. Gli specchi convessi si trovano comunemente all’interno dei parcheggi, dove i conducenti hanno bisogno di un’ampia visuale intorno agli angoli o ai potenziali punti ciechi.

Al contrario, uno specchio concavo è curvato verso l’interno e produce una riflessione ingrandita che è capovolta. Come dimostrato dalla Scuola di Fisica dell’Università del Galles del Sud, chiunque abbia un cucchiaio lucido può testare questa osservazione guardando il proprio riflesso nel cucchiaio. Sulla superficie concava del cucchiaio, dove raccogliete il vostro cibo, il vostro riflesso è distorto in modo stretto, e apparirete capovolti. Ma se girate il cucchiaio sul lato convesso, il vostro riflesso sarà dritto e più piccolo.

I riflessi variano così tanto tra superfici convesse e concave perché, sia che la superficie si curvi verso l’esterno o verso l’interno, lo specchio stesso fa parte di una sfera. Poiché la superficie di una sfera non è piatta, la luce riflessa dalla sua superficie percorrerà distanze diverse prima di contattare lo specchio.

A seconda di quale area della superficie la luce entra in contatto, un raggio di luce può riflettersi dalle superfici vicine per produrre un’area di visibilità più focalizzata. Questo è il motivo per cui, guardando la superficie interna di un cucchiaio, si potrebbe vedere solo il riflesso di ciò che è più vicino alla superficie del cucchiaio – anche se appare ancora più piccolo. Inoltre, se si dovesse mettere il dito all’interno del cucchiaio, la superficie dello specchio può produrre due o tre riflessi diversi allo stesso tempo.

Lente concava contro lente convessa

Lenti concave e convesse esistono in oggetti di uso quotidiano come occhiali, lenti a contatto, binocoli e telescopi. In modo simile alla scienza che sta dietro la riflessione della luce su specchi convessi e concavi, ci sono anche modelli di come la luce passa attraverso lenti concave e convesse per produrre un’immagine visibile.

Lenti convesse

Secondo la Manocha Academy, le lenti convesse sono chiamate lenti convergenti per la loro capacità di produrre immagini diminuite, ingrandite o introverse. La precisione con cui un’immagine appare attraverso la lente convessa dipende da quanto l’oggetto è vicino al punto focale della lente. Per qualsiasi lente convessa, ci sono punti focali simmetrici su entrambi i lati della lente.

L’accuratezza con cui un oggetto viene prodotto attraverso una lente convessa è prevista da tre principi:

Principio 1: Qualsiasi raggio di luce che passa attraverso una lente convessa è parallelo all’asse principale, che è una linea centrale che passa attraverso il centro assoluto di una lente sferica. Una volta che la luce entra in contatto con la lente, la luce si rifrange e passa attraverso il punto focale dall’altra parte. I raggi di luce che passano parallelamente all’asse principale viaggiano sopra l’oggetto davanti alla lente.

Principio 2: Qualsiasi raggio di luce che passa attraverso il centro di una lente convessa continuerà in linea retta dall’altra parte.
Principio 3: Qualsiasi raggio di luce che è passato attraverso un punto focale sullo stesso lato dell’oggetto si rifrangerà al contatto con la lente e diventerà parallelo all’asse principale sull’altro lato.

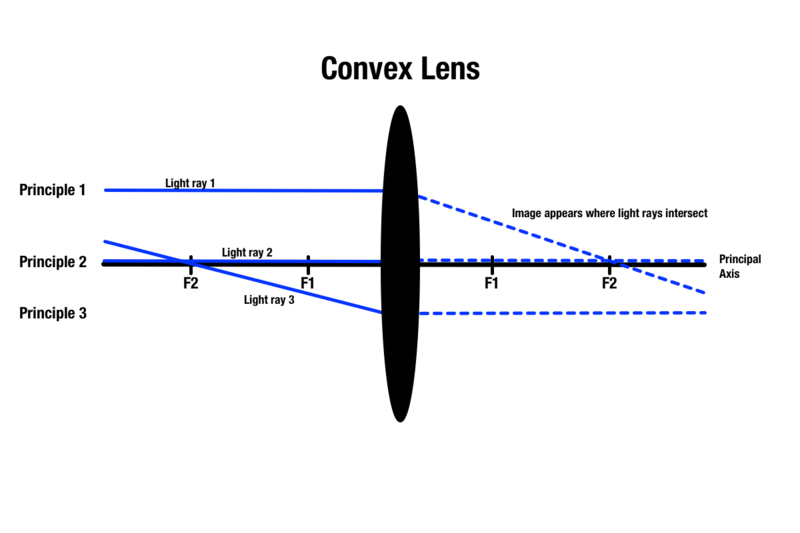
Mentre ci sono tre principi per prevedere la qualità dell’immagine attraverso una lente convessa, solo due principi possono essere applicati a un oggetto mentre si disegna un diagramma a raggi. Qualsiasi due principi produrrà un’intersezione di luce sull’altro lato della lente, che indicherà l’area in cui appare l’immagine dell’oggetto.

Più un oggetto è lontano da una lente convessa, più piccola sarà l’immagine dall’altra parte, e più un oggetto è vicino alla lente convessa, più grande apparirà. Un oggetto situato oltre il punto focale più vicino produce un’immagine più grande dietro l’oggetto. Come sottolinea Manocha Academy, questo tipo di ingrandimento della lente è usato per strumenti ottici come le lenti di ingrandimento.

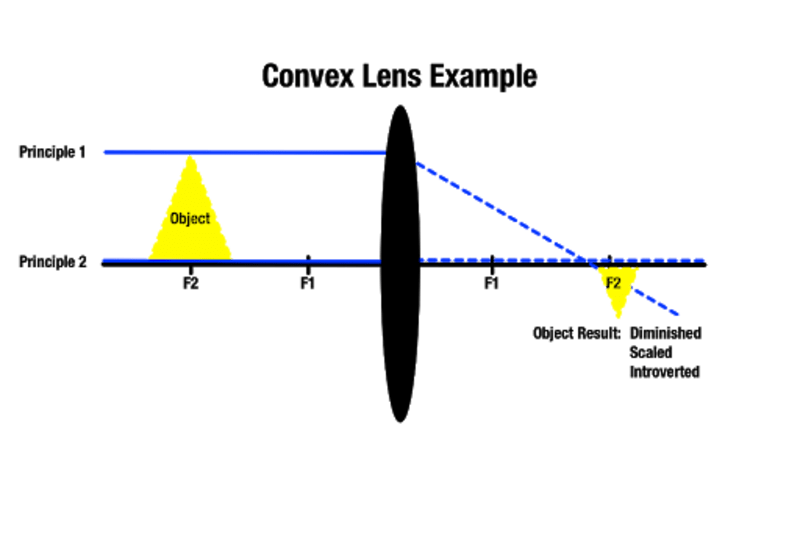
A seconda del punto focale in cui si trova un oggetto, è possibile produrre un’immagine di dimensioni approssimative. È anche possibile creare immagini reali che non sono visibili se i raggi di luce che passano non si intersecano mai perché sono paralleli dall’altra parte. In questo caso, l’immagine prodotta esiste a una distanza infinita.

Lenti concave

Ogni lente concava avrà un diametro più spesso, e un centro più sottile poiché una lente concava è curva verso l’interno. La forma delle lenti concave permette alla luce di diffondersi una volta che fa contatto con la lente, il che permette agli oggetti virtuali di apparire più piccoli. La capacità della lente concava di diffondere la luce la rende una lente ideale per strumenti come le torce, dove una fonte centrale di luce può essere utilizzata su una superficie più ampia.

Le lenti concave producono immagini con tre principi che sono simili alle lenti convesse:

Principio 1: Qualsiasi raggio di luce che viaggia sopra l’oggetto e parallelo all’asse principale si rifrange al contatto con la lente e appare come se provenisse dalla direzione del punto focale più vicino.

Principio 2: Qualsiasi raggio di luce che passa attraverso il centro della lente concava passerà senza rifrazione.
Principio 3: Qualsiasi raggio di luce diretto verso un punto focale sull’altro lato della lente concava si rifrangerà e diventerà parallelo all’asse principale.

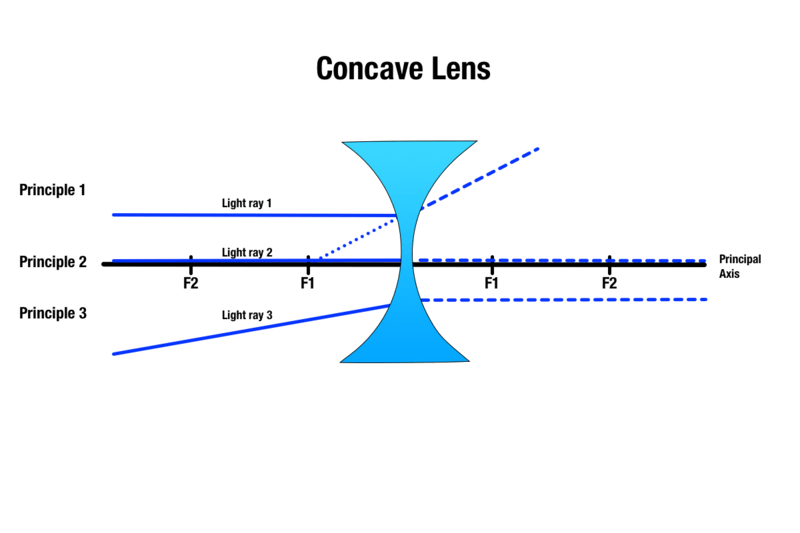
Mentre la dimensione dell’immagine dell’oggetto varia a seconda della distanza dell’oggetto da una lente concava, l’immagine prodotta è sempre virtuale, verticale, più piccola e appare sullo stesso lato della lente dell’oggetto.

Concavo vs. convesso nella scrittura

Le parole concavo e convesso sono opposte l’una all’altra, e descrivono essenzialmente la forma di oggetti o superfici nello stesso modo in cui contrapponiamo parole come:

• Piccolo vs. big
• Tall vs. short
• Slim vs. wide
• Round vs. flat

Perché concavo e convesso sono parole tecniche, usarle descrittivamente in prosa può produrre un’interpretazione più metaforica o astratta per un pubblico casuale. Ciò significa che se gli scrittori decidono di usare concavo o convesso al di fuori del loro uso tipico, lo scrittore deve decidere quanto chiaro intende essere il suo scritto.

Considera l’aggettivo

Un esempio importante dell’uso di concavo o convesso in letteratura è considerare gli scritti dell’autore americano David Foster Wallace (o DFW in breve). DFW è noto per il suo stile di scrittura complesso e tecnico – e sì, ha usato convesso e concavo per descrivere i sostantivi diverse volte. Wallace usa concavo e convesso nei seguenti esempi:

“I miei occhi erano a posto, ma non ero né grande né veloce, avevo un petto quasi concavo e polsi così sottili che potevo braccialettare con un pollice e un mignolo…”

– “Tennis, trigonometria, tornado: A Midwestern Boyhood”, Harper’s Magazine.

“…occhi di bambola che si aprono con la forza di una corda del cuore, concavi dove io sono convesso.”

– “Order and Flux in Northampton”, Conjunctions.

Il punto di usare esempi DFW non è semplicemente quello di mostrare come gli scrittori hanno usato convesso o concavo fuori dal contesto matematico, ma piuttosto, per gli scrittori di considerare se l’uso di termini tecnici o astratti è utile per comunicare chiaramente al loro pubblico.
Nel primo esempio di DFW, l’uso di concavo ha senso perché sta descrivendo la struttura di qualcosa. Ma, usare concavo e convesso per descrivere sostantivi non oggettivi, come sentimenti o pensieri, tende ad oscurare il significato di ciò che stiamo cercando di spiegare. Il secondo esempio DFW cammina su una linea sottile nell’uso di convesso e concavo perché il loro uso è sia letterale che metaforico.

FAQ: Termini correlati

Cos’è una funzione?

Una funzione è l’equazione di una linea su un grafico. Le funzioni sono diverse per ogni linea su un grafico, ma prendono la forma generale di,

f(x) = x + 1

Con qualsiasi funzione di linea, la variabile dipendente è tipicamente f(x), mentre qualsiasi variabile sconosciuta all’interno della funzione è chiamata variabile indipendente.

Cos’è il dominio?

Il dominio è un insieme di variabili indipendenti su un grafico che corrisponde alla funzione di una linea. I domini sono importanti da capire perché localizzano punti specifici sul grafico che corrisponde a qualsiasi uscita reale di un’equazione.

Cos’è l’intervallo?

L’intervallo di qualsiasi funzione rappresenta ogni possibile valore lungo l’asse x o y su un grafico che produce un valore valido per la variabile dipendente. Tutti i minimi e massimi interi sono identificati sostituendo le variabili per l’asse delle x o delle y.

Cos’è un intervallo?

Un intervallo è un insieme di numeri che rappresentano i numeri interi di una linea, ovvero il dominio. Un intervallo chiuso comprende due punti finiti di una linea, dove la linea non esiste più al di fuori dell’intervallo di un intero. Un intervallo aperto è un insieme di numeri interi che non rappresentano la fine assoluta del dominio di una linea.

Mettiti alla prova!

Vedi quanto hai capito la differenza tra convesso e concavo con le seguenti domande a scelta multipla:

1. Mentre guardi un cucchiaio lucido, noti che il tuo riflesso è capovolto. La superficie del cucchiaio è una superficie _________.
   a. Convesso
   b. Specchio
   c. Concavo
   d. Metallo
2. In termini di funzioni grafiche, una funzione convessa è talvolta chiamata:
   a. Concava verso l’alto
   b. Convessa verso il basso
   c. Concava verso il basso
   d. A e B
3. Quale delle seguenti non descrive una superficie concava:
   a. Mezza sfera cava
   b. Lente dell’occhio
   c. Ciotola per cereali
   d. Emisfero
4. Quale dei seguenti non descrive una superficie convessa:
   a. Il personaggio Stewie di Family Guy
   b. Sfera
   c. Specchio del parcheggio
   d. Calcio
5. Quale delle seguenti forme non può esistere come poligono concavo:
   a. Pentagono
   b. Esagono
   c. Triangolo
   d. Ottagono

Risposte

1. C: Concavo
2. D: A e B
3. D: Emisfero
4. B: Sfera
5. C: Triangolo

Fonti:

1. Bourne, M. “Dominio e intervallo di una funzione.” Matematica interattiva, 4 gennaio 2019.
2. “Concavo.” Dizionario Merriam-Webster, 2019.
3. “Concavo.” Il dizionario Oxford delle storie di parole, Ed. Chantrell, 2002, p. 110.
4. “Specchi concavi e convessi”. Accademia Manocha, YouTube, 2019.
5. “Lente concava: Definizione &Usi.” Study.com, 2019.
6. “Convex.” Dizionario Merriam-Webster, 2019.
7. “Lenti convesse e concave.” Accademia Manocha, YouTube, 2019.
8. “Matematica / Capire i poligoni.” Learnhive Inc., 2018.
9. “Riflessione da uno specchio concavo.” UNSW Physics, YouTube, 2017.
10. Wallace, D.F. “Tennis, trigonometria, tornado: A Midwestern Boyhood”. Harper’s Magazine, 1991.
11. Wallace, D.F. “Ordine e flusso a Northampton”. Conjunctions, 1991.
12. Weisstein, Eric W. “Funzione concava”. MathWorld-A Wolfram Web Resource, n.d.
13. Weisstein, Eric W. “Convex Function.” MathWorld-A Wolfram Web Resource, n.d.

Il Word Counter è uno strumento dinamico online usato per contare parole, caratteri, frasi, paragrafi e pagine in tempo reale, insieme al controllo ortografico e grammaticale.