Di recente, un mio collega mi ha fatto alcune domande come “perché abbiamo così tante funzioni di attivazione?”, “perché una funziona meglio dell’altra?”, “come facciamo a sapere quale usare?”, “è matematica difficile?” e così via. Così ho pensato, perché non scrivere un articolo su di esso per coloro che hanno familiarità con le reti neurali solo ad un livello di base e si stanno quindi chiedendo delle funzioni di attivazione e del loro “perché-come-matematica!”.
NOTA: Questo articolo presuppone che tu abbia una conoscenza di base di un “neurone” artificiale. Raccomando di leggere le basi delle reti neurali prima di leggere questo articolo per una migliore comprensione.
Funzioni di attivazione
Cosa fa un neurone artificiale? In poche parole, calcola una “somma pesata” del suo input, aggiunge un bias e poi decide se deve essere “licenziato” o no (sì, giusto, una funzione di attivazione fa questo, ma seguiamo il flusso per un momento).
Consideriamo quindi un neurone.
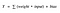
Ora, il valore di Y può essere qualsiasi cosa vada da -inf a +inf. Il neurone non conosce davvero i limiti del valore. Quindi, come decidiamo se il neurone deve sparare o no (perché questo modello di sparo? Perché l’abbiamo imparato dalla biologia che è il modo in cui funziona il cervello e il cervello è una testimonianza di lavoro di un sistema fantastico e intelligente).
A questo scopo abbiamo deciso di aggiungere delle “funzioni di attivazione”. Per controllare il valore Y prodotto da un neurone e decidere se le connessioni esterne devono considerare questo neurone come “licenziato” o no. O piuttosto diciamo – “attivato” o no.
Funzione di passo
La prima cosa che ci viene in mente è: che ne dite di una funzione di attivazione basata sulla soglia? Se il valore di Y è al di sopra di un certo valore, lo si dichiara attivato. Se è inferiore alla soglia, allora dite che non lo è. Hmm grande. Questo potrebbe funzionare!
Funzione di attivazione A = “attivata” se Y > soglia altrimenti no
Alternativamente, A = 1 se y> soglia, 0 altrimenti
Bene, quello che abbiamo appena fatto è una “funzione di passo”, vedi la figura qui sotto.
Il suo output è 1 (attivato) quando il valore > 0 (soglia) e produce uno 0 (non attivato) altrimenti. Quindi questo fa una funzione di attivazione per un neurone. Nessuna confusione. Tuttavia, ci sono alcuni inconvenienti con questo. Per capirlo meglio, pensate a quanto segue.
Supponiamo che stiate creando un classificatore binario. Qualcosa che dovrebbe dire “sì” o “no” (attivare o non attivare). Una funzione Step potrebbe farlo per voi! Questo è esattamente quello che fa, dire un 1 o uno 0. Ora, pensate al caso d’uso in cui vorreste che più neuroni di questo tipo siano collegati per portare più classi. Classe1, classe2, classe3 ecc. Cosa succederà se più di 1 neurone viene “attivato”. Tutti i neuroni emetteranno un 1 (dalla funzione step). Ora cosa deciderebbe? Quale classe è? Hmm difficile, complicato.
Vorresti che la rete attivasse solo 1 neurone e che gli altri fossero 0 (solo allora potresti dire che ha classificato correttamente/identificato la classe). È più difficile allenarsi e convergere in questo modo. Sarebbe stato meglio se l’attivazione non fosse binaria e dicesse invece “50% attivato” o “20% attivato” e così via. E poi se più di 1 neurone si attiva, si potrebbe trovare quale neurone ha “l’attivazione più alta” e così via ( meglio di max, un softmax, ma lasciamo perdere per ora ).
Anche in questo caso, se più di 1 neurone dice “100% attivato”, il problema persiste.Lo so! Ma…dato che ci sono valori di attivazione intermedi per l’uscita, l’apprendimento può essere più fluido e più facile (meno mosso) e le possibilità che più di 1 neurone sia attivato al 100% sono minori rispetto alla funzione a gradini durante l’addestramento (dipende anche da cosa si sta addestrando e dai dati).
Ok, quindi vogliamo qualcosa che ci dia valori di attivazione intermedi (analogici) piuttosto che dire “attivato” o no (binario).
La prima cosa che ci viene in mente sarebbe la funzione lineare.
Funzione lineare
A = cx
Una funzione a linea retta dove l’attivazione è proporzionale all’input (che è la somma pesata dal neurone).
In questo modo, dà una gamma di attivazioni, quindi non è attivazione binaria. Possiamo sicuramente collegare alcuni neuroni insieme e se più di 1 spara, potremmo prendere il massimo (o softmax) e decidere in base a quello. Quindi anche questo va bene. Allora qual è il problema?
Se avete familiarità con la discesa del gradiente per l’addestramento, noterete che per questa funzione, la derivata è una costante.
A = cx, la derivata rispetto a x è c. Ciò significa che il gradiente non ha alcuna relazione con X. È un gradiente costante e la discesa sarà a gradiente costante. Se c’è un errore di previsione, i cambiamenti fatti dalla retropropagazione sono costanti e non dipendono dal cambiamento dell’input delta(x)!!!
Questo non è così buono! ( non sempre, ma abbiate pazienza ). C’è anche un altro problema. Pensate agli strati collegati. Ogni strato è attivato da una funzione lineare. Quell’attivazione a sua volta va nel livello successivo come input e il secondo livello calcola la somma ponderata su quell’input e a sua volta si attiva sulla base di un’altra funzione di attivazione lineare.
Non importa quanti strati abbiamo, se tutti sono di natura lineare, la funzione di attivazione finale dell’ultimo strato non è altro che una funzione lineare dell’input del primo strato! Fermati un attimo a pensarci.
Questo significa che questi due strati (o N strati) possono essere sostituiti da un unico strato. Ah! Abbiamo appena perso la capacità di impilare gli strati in questo modo. Non importa come impiliamo, l’intera rete è ancora equivalente a un singolo strato con attivazione lineare (una combinazione di funzioni lineari in modo lineare è ancora un’altra funzione lineare).
Andiamo avanti, va bene?
Funzione sigmoidea
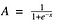
Bene, questa sembra liscia e “funzione a gradini”. Quali sono i vantaggi di questo? Pensateci un attimo. Prima di tutto, è di natura non lineare. Anche le combinazioni di questa funzione sono non lineari! Fantastico. Ora possiamo impilare gli strati. E le attivazioni non binarie? Sì, anche quello! Darà un’attivazione analogica a differenza della funzione di passo. Ha anche un gradiente liscio.
E se notate, tra i valori X da -2 a 2, i valori Y sono molto ripidi. Il che significa che qualsiasi piccolo cambiamento nei valori di X in quella regione farà cambiare significativamente i valori di Y. Ah, ciò significa che questa funzione ha la tendenza a portare i valori di Y a una delle due estremità della curva.
Sembra che sia buona per un classificatore considerando la sua proprietà? Sì, lo è davvero. Tende a portare le attivazioni ai due lati della curva (sopra x = 2 e sotto x = -2 per esempio). Facendo delle distinzioni chiare sulla predizione.
Un altro vantaggio di questa funzione di attivazione è che, a differenza della funzione lineare, l’uscita della funzione di attivazione sarà sempre nell’intervallo (0,1) rispetto a (-inf, inf) della funzione lineare. Così abbiamo le nostre attivazioni limitate in un intervallo. Bene, non farà esplodere le attivazioni allora.
Questo è fantastico. Le funzioni sigmoidi sono una delle funzioni di attivazione più utilizzate oggi. Allora quali sono i problemi con questa?
Se notate, verso le due estremità della funzione sigmoide, i valori Y tendono a rispondere molto meno ai cambiamenti in X. Cosa significa? Il gradiente in quella regione sarà piccolo. Questo dà luogo a un problema di “gradienti che svaniscono”. Hmm. Allora cosa succede quando le attivazioni raggiungono la parte “quasi orizzontale” della curva su entrambi i lati?
Il gradiente è piccolo o è svanito (non può fare cambiamenti significativi a causa del valore estremamente piccolo). La rete si rifiuta di imparare ulteriormente o è drasticamente lenta (a seconda del caso d’uso e fino a quando il gradiente / calcolo viene colpito dai limiti dei valori in virgola mobile). Ci sono modi per aggirare questo problema e la sigmoide è ancora molto popolare nei problemi di classificazione.
Funzione Tanh
Un’altra funzione di attivazione usata è la funzione tanh.
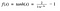
Hm. Questo sembra molto simile al sigmoide. Infatti, è una funzione sigmoide scalata!

Ok, ora questo ha caratteristiche simili alla sigmoide che abbiamo discusso sopra. È di natura non lineare, così grande che possiamo impilare gli strati! È vincolato all’intervallo (-1, 1), quindi non c’è da preoccuparsi che le attivazioni esplodano. Un punto da menzionare è che il gradiente è più forte per tanh che per sigmoide (le derivate sono più ripide). Decidere tra la sigmoide o la tanh dipenderà dalle vostre esigenze di forza del gradiente. Come la sigmoide, tanh ha anche il problema del gradiente che svanisce.
Tanh è anche una funzione di attivazione molto popolare e ampiamente usata.
ReLu
In seguito, arriva la funzione ReLu,
A(x) = max(0,x)
La funzione ReLu è come mostrato sopra. Dà un output x se x è positivo e 0 altrimenti.
A prima vista sembrerebbe avere gli stessi problemi della funzione lineare, poiché è lineare sull’asse positivo. Prima di tutto, ReLu è di natura non lineare. E anche le combinazioni di ReLu sono non lineari! ( infatti è un buon approssimatore. Qualsiasi funzione può essere approssimata con combinazioni di ReLu). Bene, quindi questo significa che possiamo impilare i livelli. Non è vincolato però. Il range di ReLu è [0, inf). Questo significa che può far saltare l’attivazione.
Un altro punto che vorrei discutere qui è la sparsità dell’attivazione. Immaginate una grande rete neurale con molti neuroni. Usare una sigmoide o una tanh farà sì che quasi tutti i neuroni si attivino in modo analogico (ricordate?). Ciò significa che quasi tutte le attivazioni saranno elaborate per descrivere l’output di una rete. In altre parole l’attivazione è densa. Questo è costoso. Idealmente vorremmo che alcuni neuroni della rete non si attivassero, rendendo così le attivazioni rade ed efficienti.
ReLu ci dà questo vantaggio. Immaginate una rete con pesi inizializzati a caso (o normalizzati) e quasi il 50% della rete produce 0 attivazioni a causa della caratteristica di ReLu (uscita 0 per valori negativi di x). Questo significa che un minor numero di neuroni sta sparando (attivazione rada) e la rete è più leggera. Woah, bello! ReLu sembra essere fantastico! Sì, lo è, ma niente è impeccabile. Nemmeno ReLu.
A causa della linea orizzontale in ReLu (per X negativo), il gradiente può andare verso 0. Per le attivazioni in quella regione di ReLu, il gradiente sarà 0 a causa del quale i pesi non verranno regolati durante la discesa. Ciò significa che i neuroni che vanno in quello stato smetteranno di rispondere alle variazioni di errore/ingresso (semplicemente perché il gradiente è 0, non cambia nulla). Questo è chiamato problema ReLu morente. Questo problema può far sì che diversi neuroni semplicemente muoiano e non rispondano rendendo una parte sostanziale della rete passiva. Ci sono variazioni in ReLu per mitigare questo problema semplicemente rendendo la linea orizzontale in componente non orizzontale. per esempio y = 0.01x per x<0 la renderà una linea leggermente inclinata piuttosto che orizzontale. Questo è il leaky ReLu. Ci sono anche altre variazioni. L’idea principale è quella di lasciare che il gradiente sia non zero e recuperare eventualmente durante l’allenamento.
ReLu è meno costoso computazionalmente di tanh e sigmoide perché comporta operazioni matematiche più semplici. Questo è un buon punto da considerare quando progettiamo reti neurali profonde.
Ok, ora quale usiamo?
Ora, quali funzioni di attivazione usare. Significa che usiamo solo ReLu per tutto quello che facciamo? O sigmoide o tanh? Beh, sì e no. Quando sapete che la funzione che state cercando di approssimare ha certe caratteristiche, potete scegliere una funzione di attivazione che approssimerà la funzione più velocemente portando ad un processo di addestramento più veloce. Per esempio, una sigmoide funziona bene per un classificatore (vedi il grafico della sigmoide, non mostra le proprietà di un classificatore ideale? ) perché approssimare una funzione di classificatore come combinazioni di sigmoide è più facile che forse ReLu, per esempio. Il che porterà ad un processo di formazione e convergenza più veloce. Potete anche usare le vostre funzioni personalizzate! Se non conoscete la natura della funzione che state cercando di imparare, allora forse vi suggerirei di iniziare con ReLu, e poi lavorare a ritroso. ReLu funziona quasi sempre come un approssimatore generale!
In questo articolo, ho cercato di descrivere alcune funzioni di attivazione usate comunemente. Ci sono anche altre funzioni di attivazione, ma l’idea generale rimane la stessa. La ricerca di funzioni di attivazione migliori è ancora in corso. Spero che abbiate capito l’idea dietro la funzione di attivazione, perché sono usate e come decidiamo quale usare.