L’algoritmo Toom-Cook
Qui impariamo un’applicazione ingegnosa di un algoritmo divide et impera combinato con l’algebra lineare per moltiplicare grandi numeri, velocemente. E un’introduzione alla notazione Big-O!
In effetti questo risultato è così controintuitivo che il grande matematico Kolmogorov ipotizzò che un algoritmo così veloce non esistesse.
Parte 0: La moltiplicazione lunga è una moltiplicazione lenta. (E un’introduzione alla notazione Big-O)
Tutti noi ricordiamo di aver imparato a moltiplicare a scuola. Infatti, ho una confessione da fare. Ricordate, questa è una zona senza giudizi 😉
A scuola, avevamo il ‘gioco bagnato’ quando pioveva troppo forte per giocare in cortile. Mentre gli altri bambini (normali/amanti del divertimento/positivo-aggettivo-di-scelta) giocavano e facevano casino, a volte prendevo un foglio di carta e moltiplicavo grandi numeri insieme, solo per il gusto di farlo. La pura gioia del calcolo! Avevamo anche una gara di moltiplicazione, la ‘Super 144’, in cui dovevamo moltiplicare una griglia di numeri (da 1 a 12) strapazzata nel minor tempo possibile. Mi esercitavo religiosamente, al punto che avevo i miei fogli di pratica pre-preparati che fotocopiavo e poi usavo a rotazione. Alla fine riuscii ad abbassare il mio tempo a 2 minuti e 1 secondo, al che fu raggiunto il mio limite fisico di scarabocchiare.
Nonostante questa ossessione per la moltiplicazione, non mi venne mai in mente che si potesse fare meglio. Ho passato tante ore a moltiplicare, ma non ho mai cercato di migliorare l’algoritmo.
Considera la moltiplicazione di 103 per 222.
Calcoliamo 2 volte 3 volte 1 +2 volte 0 volte 10 + 2 volte 1 volte 100 + 20 volte 3 volte 1 + 20 volte 0 volte 10 + 20 volte 1 volte 100 = 22800
In generale, per moltiplicare a n numeri di cifre, ci vuole O(n²) operazioni. La notazione ‘big-O’ significa che, se dovessimo tracciare un grafico del numero di operazioni in funzione di n, il termine n² è quello che conta davvero. La forma è essenzialmente quadratica.
Oggi realizzeremo tutti i nostri sogni d’infanzia e miglioreremo questo algoritmo. Ma prima! Big-O ci aspetta.
Big-O
Guarda i due grafici qui sotto

Chiedete a un matematico, “x² e x²+x^(1/3) sono uguali?”, e probabilmente vomiteranno nella loro tazza di caffè e inizieranno a piangere, e borbotteranno qualcosa sulla topologia. Almeno, questa è stata la mia reazione (all’inizio), e non so quasi nulla di topologia.
Ok. Non sono la stessa cosa. Ma al nostro computer non interessa la topologia. I computer differiscono nelle prestazioni in così tanti modi che non posso nemmeno descrivere perché non so nulla di computer.
Ma non ha senso mettere a punto un rullo compressore. Se due funzioni, per grandi valori del loro input, crescono allo stesso ordine di grandezza, allora per scopi pratici questo contiene la maggior parte delle informazioni rilevanti.
Nel grafico sopra, vediamo che le due funzioni sembrano abbastanza simili per grandi input. Ma allo stesso modo, x² e 2x² sono simili – il secondo è solo due volte più grande del primo. A x = 100, uno è 10.000 e uno è 20.000. Questo significa che se possiamo calcolare uno, probabilmente possiamo calcolare l’altro. Mentre una funzione che cresce esponenzialmente, diciamo 10^x, a x = 100 è già molto più grande del numero di atomi nell’universo. (10¹⁰⁰ >>> 10⁸⁰ che è una stima, il numero di Eddington, sul numero di atomi nell’universo secondo il mio Google*).
*in realtà, ho usato DuckDuckGo.
Scrivere interi come polinomi è sia molto naturale che molto innaturale. Scrivere 1342 = 1000 + 300 + 40 + 2 è molto naturale. Scrivere 1342 = x³+3x²+4x + 2, dove x = 10, è leggermente strano.
In generale, supponiamo di voler moltiplicare due grandi numeri, scritti in base b, con n cifre ciascuno. Scriviamo ogni numero di n cifre come un polinomio. Se dividiamo il numero di n cifre in r pezzi, questo polinomio ha n/r termini.
Per esempio, facciamo b = 10, r = 3, e il nostro numero è 142.122.912
Possiamo trasformarlo in
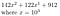
Questo funziona molto bene quando r = 3 e il nostro numero, scritto in base 10, ha 9 cifre. Se r non divide perfettamente n, allora possiamo semplicemente aggiungere degli zeri davanti. Di nuovo, questo è meglio illustrato da un esempio.
27134 = 27134 + 0*10⁵ = 027134, che rappresentiamo come
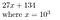
Perché questo potrebbe essere utile? Per trovare i coefficienti del polinomio P, se il polinomio è di ordine N, allora campionandolo in N+1 punti possiamo determinare i suoi coefficienti.
Per esempio, se il polinomio x⁵ + 3x³ +4x-2, che è di ordine 5, viene campionato in 6 punti, possiamo poi elaborare l’intero polinomio.
Intuitivamente, un polinomio di ordine 5 ha 6 coefficienti: il coefficiente di 1, x, x², x³, x⁴, x⁵. Dati 6 valori e 6 incognite, possiamo scoprire i valori.
(Se conoscete l’algebra lineare, potete trattare le diverse potenze di x come vettori linearmente indipendenti, fare una matrice per rappresentare l’informazione, invertire la matrice, e voilà)
Campionare i polinomi per determinare i coefficienti (Opzionale)
Qui guardiamo un po’ più in profondità la logica dietro al campionamento di un polinomio per dedurre i suoi coefficienti. Sentitevi liberi di passare alla prossima sezione.
Quello che mostreremo è che, se due polinomi di grado N concordano su N+1 punti, allora devono essere uguali. Cioè N+1 punti specificano univocamente un polinomio di ordine N.
Consideriamo un polinomio di ordine 2. Questo è della forma P(z) = az² +bz + c. Per il teorema fondamentale dell’algebra – senza vergogna, qui ho passato diversi mesi a mettere insieme una prova di questo, e poi a scriverla, qui – questo polinomio può essere fattorizzato. Ciò significa che possiamo scriverlo come A(z-r)(z-w)
Nota che a z = r, e a z = w, il polinomio si valuta a 0. Diciamo che w e r sono radici del polinomio.
Ora dimostriamo che P(z) non può avere più di due radici. Supponiamo che abbia tre radici, che chiamiamo w, r, s. Poi fattorizziamo il polinomio. P(z) = A(z-r)(z-w). Allora P(s) = A(s-r)(s-w). Questo non è uguale a 0, perché moltiplicando i numeri non nulli si ottiene un numero non nullo. Questa è una contraddizione perché la nostra ipotesi originale era che s fosse una radice del polinomio P.
Questo argomento può essere applicato a un polinomio di ordine N in modo essenzialmente identico.
Ora, supponiamo che due polinomi P e Q di ordine N concordino su N+1 punti. Allora, se sono diversi, P-Q è un polinomio di ordine N che è 0 in N+1 punti. Per il precedente, questo è impossibile, poiché un polinomio di ordine N ha al massimo N radici. Quindi, la nostra supposizione deve essere sbagliata, e se P e Q concordano su N+1 punti sono lo stesso polinomio.
Vedere è credere: A Worked Example
Guardiamo un numero veramente enorme che chiamiamo p. In base 10, p è lungo 24 cifre (n=24), e lo divideremo in 4 pezzi (r=4). n/r = 24/4 = 6
p = 292,103,243,859,143,157,364,152.
E lasciamo che il polinomio che lo rappresenta si chiami P,
P(x) = 292,103 x³ + 243,859 x² +143,157 x+ 364,152
con P(10⁶) = p.
Poiché il grado di questo polinomio è 3, possiamo calcolare tutti i coefficienti dal campionamento a 4 punti. Vediamo cosa succede quando lo campioniamo in alcuni punti.
- P(0) = 364.152
- P(1) = 1.043.271
- P(-1) = 172.751
- P(2) = 3.962.726
Un aspetto sorprendente è che tutti questi hanno 6 o 7 cifre. Questo rispetto alle 24 cifre che si trovano originariamente in p.
Moltipliciamo p per q. Facciamo q = 124,153,913,241,143,634,899,130, e
Q(x) = 124,153 x³ + 913,241 x²+143,634 x + 899,130
Calcolare t=pq potrebbe essere orribile. Ma invece di farlo direttamente, proviamo a calcolare la rappresentazione polinomiale di t, che etichettiamo T. Poiché P è un polinomio di ordine r-1=3, e Q è un polinomio di ordine r-1 = 3, T è un polinomio di ordine 2r-2 = 6.
T(10⁶) = t = pq
T(10⁶) = P(10⁶)Q(10⁶)
Il trucco consiste nell’elaborare i coefficienti di T, piuttosto che moltiplicare direttamente p e q insieme. Quindi, calcolare T(1⁰⁶) è facile, perché per moltiplicare per 1⁰⁶ basta mettere 6 zeri sul retro. Sommare tutte le parti è anche facile perché l’addizione è un’azione a bassissimo costo per i computer.
Per calcolare i coefficienti di T, dobbiamo campionarlo in 2r-1 = 7 punti, perché è un polinomio di ordine 6. Probabilmente vogliamo scegliere piccoli numeri interi, quindi scegliamo
- T(0)=P(0)Q(0)= 364.152*899.130
- T(1)=P(1)Q(1)= 1.043.271*2.080.158
- T(2)=P(2)Q(2)= 3.962.726*5.832,586
- T(-1)=P(-1)Q(-1)= 172751*1544584
- T(-2)=P(-2)Q(-2)= -1.283.550*3.271,602
- T(3)=P(-3)Q(-3)= -5.757.369*5.335.266
Nota la dimensione di P(-3), Q(-3), P(2), Q(2) ecc. Questi sono tutti numeri con circa n/r = 24/4 = 6 cifre. Alcuni sono di 6 cifre, altri di 7. Man mano che n diventa più grande, questa approssimazione diventa sempre più ragionevole.
Finora abbiamo ridotto il problema ai seguenti passi, o algoritmo:
(1) Prima calcoliamo P(0), Q(0), P(1), Q(1), ecc (azione a basso costo)
(2) Per ottenere i nostri 2r-1= 7 valori di T(x), dobbiamo ora moltiplicare 2r-1 numeri di dimensione approssimativa lunga n/r cifre. Vale a dire, dobbiamo calcolare P(0)Q(0), P(1)Q(1), P(-1)Q(-1), ecc. (Azione ad alto costo)
(3) Ricostruire T(x) dai nostri punti dati. (Azione a basso costo: ma entrerà in considerazione più tardi).
(4) Con la nostra T(x) ricostruita, valutare T(10⁶) in questo caso
Questo porta piacevolmente all’analisi del tempo di esecuzione di questo approccio.
Tempo di esecuzione
Da quanto sopra, abbiamo scoperto che, ignorando temporaneamente le azioni a basso costo (1) e (3), il costo della moltiplicazione di due numeri a n cifre con l’algoritmo di Toom obbedirà:
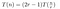
Questo è quanto abbiamo visto nell’esempio lavorato. Moltiplicare ogni P(0)Q(0), P(1)Q(1), ecc. costa T(n/r) perché stiamo moltiplicando due numeri di lunghezza circa n/r. Dobbiamo farlo 2r-1 volte, poiché vogliamo campionare T(x) – essendo un polinomio di ordine 2r-2 – in 2r-1 punti.
Quanto è veloce? Possiamo risolvere esplicitamente questo tipo di equazione.

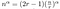
Tutto ciò che rimane ora è un po’ di algebra incasinata
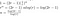
Come ci sono stati alcuni altri costi dal processo di moltiplicazione (‘riassemblaggio’) della matrice, e dall’addizione, non possiamo davvero dire che la nostra soluzione è il runtime esatto, così invece concludiamo che abbiamo trovato il big-O del runtime
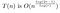
Ottimizzando r
Questo runtime dipende ancora da r. Fissiamo r e abbiamo finito. Ma la nostra curiosità non è ancora soddisfatta!
Quando n diventa grande, vogliamo trovare un valore approssimativamente ottimale per la nostra scelta di r. Cioè vogliamo scegliere un valore di r che cambi per diversi valori di n.
La cosa chiave qui è che, con r che varia, dobbiamo fare attenzione al costo di riassemblaggio – la matrice che esegue questa operazione ha un costo di O(r²). Quando r è fisso, non dobbiamo guardare a questo, perché quando n diventa grande con r fisso, sono i termini che coinvolgono n a determinare la crescita di quanto calcolo è richiesto. Poiché la nostra scelta ottimale di r diventerà più grande man mano che n diventa più grande, non possiamo più ignorare questo fatto.
Questa distinzione è cruciale. Inizialmente la nostra analisi ha scelto un valore di r, forse 3, forse 3 miliardi, e poi ha guardato la dimensione di big-O man mano che n cresceva arbitrariamente. Ora, guardiamo il comportamento mentre n cresce arbitrariamente grande e r cresce con n a qualche tasso che determiniamo. Questo cambio di prospettiva guarda O(r²) come una variabile, mentre quando r era tenuto fisso, O(r²) era una costante, anche se non la conoscevamo.
Quindi, aggiorniamo la nostra analisi di prima:
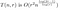
dove O(r²) rappresenta il costo della matrice di riassemblaggio. Vogliamo ora scegliere un valore di r per ogni valore di n, che minimizzi approssimativamente questa espressione. Per minimizzare, proviamo prima a differenziare rispetto a r. Questo dà l’espressione dall’aspetto un po’ odioso

Normalmente, per trovare il punto minimo, impostiamo la derivata uguale a 0. Ma questa espressione non ha un bel minimo. Invece, troviamo una soluzione “abbastanza buona”. Usiamo r = r^(sqrt(logN)) come valore stimato. Graficamente, questo è abbastanza vicino al minimo. (Nel diagramma qui sotto, il fattore 1/1000 è lì per rendere il grafico visibile in scala ragionevole)
Il grafico qui sotto mostra la nostra funzione per T(N), scalata da una costante, in rosso. La linea verde è a x = 2^sqrt(logN) che era il nostro valore stimato. ‘x’ prende il posto di ‘r’, e in ciascuna delle tre immagini, viene usato un diverso valore di N.



Questo è abbastanza convincente per me che la nostra scelta è stata buona. Con questa scelta di r, possiamo inserirlo e vedere come il big-O finale del nostro algoritmo:

dove abbiamo semplicemente inserito il nostro valore per r, e usato un’approssimazione per log(2r-1)/log(r) che è molto accurata per grandi valori di r.
Quanto è migliorato?
Forse è stato ragionevole che non mi sia accorto di questo algoritmo quando ero un ragazzino che faceva le moltiplicazioni. Nel grafico qui sotto, do il coefficiente della nostra funzione big-O a 10 (a scopo dimostrativo) e lo divido per x² (poiché l’approccio originale alla moltiplicazione era O(n²). Se la linea rossa tende a 0, questo mostrerebbe che il nostro nuovo tempo di esecuzione fa asintoticamente meglio di O(n²).
E in effetti, mentre la forma della funzione mostra che il nostro approccio è alla fine più veloce, e alla fine è molto più veloce, dobbiamo aspettare di avere numeri lunghi quasi 400 cifre perché questo sia il caso! Anche se il coefficiente fosse solo 5, i numeri dovrebbero essere lunghi circa 50 cifre per vedere un miglioramento della velocità.

Per il mio io di 10 anni, moltiplicare numeri di 400 cifre sarebbe un po’ difficile! Tenere traccia delle varie chiamate ricorsive della mia funzione sarebbe anche un po’ scoraggiante. Ma per un computer che svolge un compito in IA o in fisica, questo è un problema comune!
Quanto è profondo questo risultato?
Quello che amo di questa tecnica è che non è scienza missilistica. Non è la matematica più sbalorditiva che sia mai stata scoperta. Con il senno di poi, forse appare ovvio!
Tuttavia, questa è la genialità e la bellezza della matematica. Ho letto che Kolmogorov congetturò in un seminario che la moltiplicazione era fondamentalmente O(n²). Kolmogorov ha fondamentalmente inventato un sacco di teoria della probabilità e analisi moderna. È stato uno dei grandi matematici del 20° secolo. Eppure, quando si trattava di questo campo non correlato, si è scoperto che c’era un intero corpus di conoscenze in attesa di essere scoperto, proprio sotto il suo naso e quello di tutti gli altri!
In effetti, gli algoritmi Divide et Conquer vengono in mente abbastanza rapidamente oggi, dato che sono così comunemente usati. Ma sono un prodotto della rivoluzione informatica, in quanto è solo con la grande potenza di calcolo che le menti umane si sono concentrate specificamente sulla velocità di calcolo come un’area della matematica degna di essere studiata a pieno titolo.
Questo è il motivo per cui i matematici non sono semplicemente disposti ad accettare che l’Ipotesi di Riemann sia vera solo perché sembra che potrebbe essere vera, o che P non è uguale a NP solo perché questo sembra più probabile. Il meraviglioso mondo della matematica conserva sempre una capacità di confondere le nostre aspettative.
In effetti, è possibile trovare modi ancora più veloci per moltiplicare. I migliori approcci attuali usano le trasformate veloci di Fourier. Ma lo conserverò per un altro giorno 🙂
Fammi sapere i tuoi pensieri qui sotto. Sono da poco su Twitter come ethan_the_mathmo, puoi seguirmi qui.
Mi sono imbattuto in questo problema in un meraviglioso libro che sto usando chiamato ‘The Nature of Computation’ dei fisici Moore e Mertens, dove uno dei problemi ti guida attraverso l’analisi dell’algoritmo di Toom.