Come aiutare gli studenti che lottano con i problemi di parole

“Conoscono la matematica. Solo che non possono fare i problemi di parole. È la loro comprensione della lettura.”

La signora Hartwell stava spiegando perché i suoi studenti avevano faticato nei test statali. Conosceva i suoi studenti e aveva fatto un’ampia valutazione. Era sicura che le loro difficoltà fossero un problema di alfabetizzazione.

“Non capisco perché rendono la lettura così difficile. I ragazzi fanno già un test di lingua.”

Sono stato abbinato alla signora Hartwell (e ad altri nella sua scuola) come parte di un programma di New York City per aumentare i risultati in matematica. L’obiettivo era quello di portare la matematica concettuale nelle scuole “Tier 1”. Le scuole di livello 1 erano quelle che guidavano la città in tre aree. Reddito più basso, punteggi più bassi nei test, e la più alta percentuale di studenti di colore.

Ho sentito la spiegazione “alfabetizzazione” da altri insegnanti del programma. E aveva senso. Se gli studenti conoscevano la matematica, perché altrimenti stavano lottando nel test, che aveva molti problemi di parole?

Ma c’era una fregatura. Negli ultimi tre anni, il livello di alfabetizzazione era passato dal 30% al 40%, in tutta la città. Nello stesso periodo, i punteggi di matematica erano rimasti per lo più piatti.

Se questo fosse un problema di lettura, l’aumento dei punteggi di lettura dovrebbe sbloccare una crescita esplosiva in matematica. Inoltre, il linguaggio nei problemi di parole non sembrava abbastanza complicato da causare problemi.

Il periodo successivo, avevo in programma di visitare la classe della signora Hartwell. Aveva programmato una lezione sui problemi di parole, così potevo vedere il problema in prima persona.

Over-Scaffolding Word Problems

Gli studenti sedevano in tavoli rotondi, e lei stava in piedi davanti. Lei e i suoi studenti avevano tutti delle lavagne portatili.

Hanno aperto i loro libri di testo a pagina 47 e lei ha letto un problema di parole ad alta voce. “Sarah ha 40 libbre di carote per i suoi cavalli. Se ha 100 cavalli, quante libbre prende ogni cavallo?

“OK classe, lei ha 40 libbre che darà ad ogni cavallo. Quindi di quale operazione abbiamo bisogno?”.

Ha indicato una tabella di ancoraggio che elencava le ‘parole chiave’ per ogni operazione. Ciascuna’ era in cima alla lista della divisione.

“Divisione!” rispose la classe.

“Giusto. Quindi come dividiamo un numero piccolo per un numero grande?”

La classe era tranquilla. La signora Hartwell disegnò un vinculum (casa di divisione lunga) sulla sua lavagna. Gli studenti copiarono mentre lei metteva 40 sotto la casa e 100 fuori.

“Ora 100 non entra in 40, quindi abbiamo bisogno di aggiungere un decimale”. Ha cambiato 40 in 40,0. “Quante volte 100 entra in 400?”.

Alcuni studenti gridarono “Quattro!”.

“Esattamente. Ora dobbiamo mettere un decimale anche nel nostro quoziente. La nostra risposta finale è?”

La classe ha letto la risposta, “0,4,” dalla sua lavagna bianca.

Ha assegnato un problema simile, e ha indicato il poster “CUBES” sul muro. “Ricordatevi di cerchiare i numeri e di mettere nel riquadro le parole chiave”

Circolava mentre gli studenti lavoravano. Alcuni hanno chiesto dove mettere il decimale. Altri avevano problemi ad allineare la parte di sottrazione della divisione lunga. Alcuni studenti lavoravano in coppia, con uno che faceva i calcoli, mentre l’altro copiava.

Per la fine della lezione, tutti avevano la risposta corretta sul loro foglio. “Vedi?

Cosa è andato storto?

Mentre questo è un esempio estremo, molti degli errori commessi dalla signora Hartwell sono in realtà piuttosto comuni.

L’eccessivo sostegno si verifica quando forniamo agli studenti troppo supporto. Mentre è comune per gli educatori essere orgogliosi di fornire agli studenti “tutto il supporto di cui hanno bisogno”, l’overscaffolding è diverso.

Il termine “scaffolding” deriva dal lavoro di Lev Vygotsky. Ha coniato il termine “Zona di sviluppo prossimale”. La ZPD include cose che sono appena fuori dalla portata di uno studente. Non possono farlo da soli, ma possono farlo con il supporto. Tramite l'”impalcatura”, possiamo spostare queste abilità nel set di abilità principali di uno studente.

Quello che viene spesso trascurato è che l’impalcatura si applica solo alle abilità già nella ZPD di uno studente. Ci sono un’intera gamma di abilità che sono attualmente fuori dalla portata di uno studente. Quando tentiamo di rinforzare queste abilità, facciamo più male che bene.

Un problema con l’eccesso di scaffolding è che gli studenti non interiorizzano mai le abilità mirate. Quando aiutiamo uno studente con qualcosa al di fuori del suo ZPD, avrà sempre bisogno del nostro aiuto. Almeno fino a quando non identifichiamo le abilità intermedie che sono nella loro ZPD.

Un altro problema è che l’over-scaffolding ci dà un falso senso di successo. In questo caso, la signora Hartwell credeva che i suoi studenti potessero ‘fare la matematica’ nel problema di parole. In realtà, stavano solo imitando le sue azioni. Non c’era motivo di credere che potessero trovare una soluzione simile da soli.

Ha anche rimosso l’intero processo di ‘formulazione’ dal processo di risoluzione dei problemi. Molti educatori pensano alla comprensione e alla formulazione come la stessa cosa, ma la formulazione è una competenza matematica separata.

E potrebbe essere l’ingrediente mancante nel modo in cui attualmente insegnate i problemi di parole.

Risorse per l’aula e apprendimento professionale

Formulazione: La chiave del successo con i problemi di parole

Formulare i problemi di parole implica la loro comprensione. Ma va oltre questo. La formulazione è più simile alla traduzione che alla comprensione.

Quando uno studente legge un problema di parole, prima deve trasformare le lettere in suoni (decodifica). Poi, deve capire il significato delle parole (vocabolario). Deve capire come le parole stanno insieme in una frase (sintassi). Infine, la comprensione deriva dal mettere insieme questi pezzi per dare un significato.

La maggior parte degli studenti del sesto grado potrebbe leggere il problema della signora Hartwell e capire facilmente che Sarah sta distribuendo carote ai suoi cavalli. Ma molti meno collegheranno la “condivisione” delle carote alla divisione.

Questa è la parte che fa inciampare molti educatori. Ci sembra così ovvio. “Sta letteralmente dividendo le carote. Come possono non vedere che è una divisione”.

Non lo fanno e basta. Se lo facessero, non si vedrebbero tabelle di parole chiave appese nelle aule di matematica. E tutto risale a quando insegniamo le operazioni per la prima volta.

Perché gli studenti lottano con la formulazione

Molti insegnanti in molte scuole insegnano agli studenti che la matematica è una materia di creazione di senso. Ma in altre, la matematica è insegnata come una materia per ricordare.

Un esempio di ‘matematica come ricordare’ è quando gli studenti memorizzano i fatti matematici. Ma anche gli algoritmi servono a ricordare. Metti 120 sopra 47. Segui questi passi per aggiungere, questi per sottrarre, e questi per moltiplicare.

Gli studenti possono ripetere questi passi senza capire la grandezza dei numeri o anche il significato delle operazioni.

Quando iniziamo con i concetti (usando modelli visivi o frasi sui numeri), gli studenti imparano il significato delle operazioni. Quando passiamo direttamente ad un algoritmo, gli studenti pensano alle operazioni come ad una serie di passi casuali.

Anno dopo anno, facciamo ricordare e ripetere agli studenti. Completano lo stesso algoritmo 30 volte per i compiti. Cambia i numeri e il processo rimane lo stesso. Ma dai loro un problema di parole, e ora devono dare un senso.

Cosa ci dicono i test sul ragionamento

Potremmo dare ai nostri studenti 10 problemi con il titolo “Problemi di divisione”, per rendere tutto più facile. Non avranno nemmeno bisogno di leggere i problemi. Hanno solo bisogno di capire (o indovinare) quale numero è il divisore e quale il dividendo.

Ma quando gli studenti fanno un test di stato, l’obiettivo non è quello di renderlo più facile. L’obiettivo è quello di valutare cosa possono fare da soli.

Costruttori di test non vogliono dire loro quale operazione usare. Metteranno persino parole chiave per la divisione e l’addizione nello stesso problema. “Ci sono 20 studenti nella classe. Se ogni bambino ha tre dollari, quanto hanno in totale?”.

Quindi quando gli studenti lottano con i problemi di parole, non si tratta solo dei problemi di parole. Di solito significa che stanno facendo matematica a memoria. Abbiamo bisogno di insegnare loro che la matematica riguarda la creazione di senso.

Gli studenti hanno bisogno di strategie e processi per risolvere i problemi di parole

Parte del problema con un sistema come CUBES è che si definisce una strategia, ma è davvero un processo.

Un processo è una serie di passi. Una volta identificato un processo efficiente, puoi ripeterlo ancora e ancora senza pensarci troppo. Gli algoritmi sono un processo. Come lo è allineare “dal più alto al più basso” per la passeggiata verso il pranzo.

Una strategia è diversa. Le strategie richiedono una comprensione profonda. E la capacità di applicare la comprensione in nuove situazioni.

Non possiamo preparare gli studenti per ogni scenario che incontreranno in un problema di parole. Alcuni richiedono di combinare diverse abilità matematiche che non hanno mai combinato prima. O possono richiedere che gli studenti cambino l’ordine dei passi per arrivare alla soluzione corretta.

Considera quanto segue:

Hai 5 galloni di succo per un evento scolastico con 100 studenti. Se ogni tazza contiene 3 once, quante tazze può bere ogni studente? Quanto ne rimarrà?

Un processo di problem-solving può aiutare gli studenti ad affrontare questo problema. “Identificare ciò che viene chiesto”. “Considera quali informazioni vengono date.”

Ma non c’è un processo fisso che possiamo insegnare loro per risolverlo davvero. È qui che entra in gioco la strategia. Hanno bisogno di convertire le unità. Riconoscere che stiamo dividendo con i resti, piuttosto che dividere completamente. Probabilmente dovrebbero anche riordinare le operazioni, dividendo il succo in tazze prima di dividere per il numero di studenti.

Non c’è nessun “trucco” che porterà gli studenti lì. Hanno bisogno di capire il significato delle operazioni. Hanno bisogno di capire la matematica come soggetto di creazione di senso. E hanno bisogno di fare pratica ripetuta applicando il pensiero strategico ai problemi di parole.

Il processo di Polya per risolvere i problemi di parole

George Pólya era un influente matematico ungherese e professore di Stanford che trovò un processo che poteva essere usato per risolvere qualsiasi problema. Il suo lavoro ha toccato innumerevoli matematici ed educatori, la maggior parte dei quali non conosce il suo nome.

In effetti, CUBES e altre cosiddette strategie di problem solving sono vagamente basate sul suo lavoro. Il problema è che cercano di semplificarlo. Nel processo, rimuovono tutto ciò che assomiglia al pensiero profondo.

Polya credeva che ogni problema potesse essere risolto in quattro passi: Capire, Pianificare, Risolvere e Riflettere. Penso che il processo originale di Polya in quattro fasi vada bene per l’uso nelle scuole.

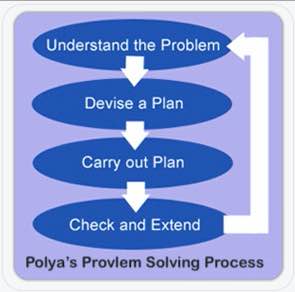Per capire il problema, identifichiamo quali informazioni sono date e cosa vogliamo trovare. È da qui che provengono la ‘C’ e la ‘U’ dei cubi. Se gli studenti vogliono cerchiare i numeri e sottolineare la domanda, bene. Preferisco che li scrivano (con le unità) in un organizzatore grafico, almeno all’inizio. Questo li aiuta ad elaborare ciò che stanno leggendo. Mi aiuta anche, come insegnante, a valutare la loro comprensione mentre cammino per la stanza.

La prossima è la parte difficile. Il ‘piano’ è dove formuliamo il problema. Stiamo prendendo uno scenario del mondo reale e lo trasformiamo in un’altra rappresentazione matematica.

Il terzo passo è risolvere. Se abbiamo formulato correttamente, qui è dove calcoliamo. Gli studenti di solito usano un algoritmo, ma io incoraggio a usare anche equazioni e modelli visivi.

Infine, gli studenti guardano indietro e controllano il loro lavoro. Dovrebbero anche riflettere sul loro processo. Se ho fatto un errore, perché? Questa strategia potrebbe aiutarmi a risolvere problemi simili in futuro?

Strategie per risolvere i problemi di parole

Avere un processo per affrontare i problemi di parole è sicuramente utile. Ma non possiamo pretendere che la matematica significativa si impari solo seguendo dei passi. Lo scopo dei problemi di parole è quello di espandere la matematica oltre i “fatti matematici” e gli algoritmi.

Ci sono alcune strategie utili per aiutare gli studenti con la formulazione. All’inizio, insegno esplicitamente una serie di strategie diverse.

Come insegno le strategie, faccio risolvere agli studenti problemi che vanno bene con quella strategia. Alcuni tipi di problemi vanno molto bene con ‘Indovina e controlla’. Altri sono più adatti a “Disegna un’immagine”.

Finalmente, do loro problemi di parole impegnativi che possono essere risolti in diversi modi. Una volta che hanno gli strumenti nelle loro cinture, possono scegliere il migliore per la situazione.

Combinare le strategie può anche essere molto efficace. Per esempio, disegnare un’immagine può spesso essere utile per aiutare la formulazione. Se un contadino ha 18 file di carote e 10 carote in ogni fila, uno studente può iniziare disegnando il campo. Ad un certo punto, possono pensare “Wow, questo è un array”, e realizzare che possono moltiplicare usando la matematica mentale, un’espressione o un algoritmo.

Altre volte, gli studenti possono usare modelli visivi per formulare e risolvere il problema.

Aiutate i vostri studenti ad affrontare problemi di parole impegnativi

Se siete come molti insegnanti, potreste essere preoccupati di come i vostri studenti affronteranno tutto questo. Processi, strategie, pensiero critico… c’è molto da fare.

Potresti anche pensare che i problemi di parole sembravano più facili prima di questo articolo. Se è così, mi scuso.

La chiave è non farsi sopraffare cercando di fare tutto in una volta. Iniziate a risolvere un semplice problema di parole usando il processo di Polya. Poi, introduci una nuova strategia ogni settimana. Entro la fine dell’anno, sarai stupito di quanto lontano siano arrivati.

Forse sei interessato ad approfondire la risoluzione creativa dei problemi. Considera la possibilità di frequentare un workshop di matematica pratica o di lavorare con un coach online.

Se sei pronto a portare un po’ di Polya nella tua classe domani, questo organizzatore grafico è un ottimo modo per iniziare. Esso vi aiuterà a sostenere il processo in quattro fasi e a identificare dove i vostri studenti stanno andando fuori strada.

Organizzatore di problemi di parole gratis

Sull’autore

Jeff Lisciandrello è il fondatore di Room to Discover e un consulente educativo specializzato nell’apprendimento centrato sullo studente. Il suo 3-Bridges Design for Learning aiuta le scuole ad esplorare pratiche innovative all’interno delle impostazioni tradizionali. Si diverte ad aiutare gli educatori ad abbracciare approcci basati sull’indagine e personalizzati all’istruzione. Potete connettervi con lui su Twitter @EdTechJeff

.