A közelmúltban egy kollégám feltett nekem néhány kérdést, például “miért van ennyi aktiválási függvényünk?”.”, “miért van az, hogy az egyik jobban működik, mint a másik?”, “honnan tudjuk, hogy melyiket használjuk?”, “ez hardcore matematika?” stb. Ezért gondoltam, miért ne írnék erről egy cikket azoknak, akik csak alapszinten ismerik a neurális hálózatot, és ezért kíváncsiak az aktiválási függvényekre és azok “miért-hogyan-matematikájára!”.
MEGJEGYZÉS: Ez a cikk feltételezi, hogy rendelkezel alapismeretekkel a mesterséges “neuronról”. Javaslom, hogy a cikk elolvasása előtt olvassa el a neurális hálózatok alapjait a jobb megértés érdekében.
Aktivációs függvények
Szóval, mit csinál egy mesterséges neuron? Egyszerűen fogalmazva, kiszámítja a bemenetének “súlyozott összegét”, hozzáad egy torzítást, majd eldönti, hogy “tüzelni” kell-e vagy sem ( igen, igaz, ezt egy aktiválási függvény végzi, de egy pillanatra haladjunk az árral ).
Ezért tekintsünk egy neuront.
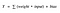
Most, Y értéke bármi lehet -inf és +inf között. A neuron valójában nem ismeri az érték határait. Hogyan döntjük el tehát, hogy a neuron tüzeljen-e vagy sem ( miért ez a tüzelési minta? Mert a biológiából tanultuk, hogy így működik az agy, és az agy egy félelmetes és intelligens rendszer működő tanúbizonysága ).
Ezért úgy döntöttünk, hogy “aktiválási függvényeket” adunk hozzá. Hogy ellenőrizzük egy neuron által termelt Y értéket, és eldöntsük, hogy a külső kapcsolatok ezt a neuront “kilőttnek” tekintsék-e vagy sem. Vagy inkább mondjuk úgy – “aktivált” vagy nem.
Szintfüggvény
Az első dolog, ami eszünkbe jut, hogy mi lenne, ha egy küszöbérték alapú aktivációs függvényt használnánk? Ha Y értéke egy bizonyos érték felett van, nyilvánítsuk aktiváltnak. Ha a küszöbérték alatt van, akkor mondjuk, hogy nem. Hmm nagyszerű. Ez működhet!
Az aktiválási függvény A = “aktivált”, ha Y > küszöbérték, különben nem
Alternatívaként A = 1, ha y> küszöbérték, 0 egyébként
Nos, amit most csináltunk, az egy “lépésfüggvény”, lásd az alábbi ábrát.
A kimenete 1 ( aktivált), ha az érték > 0 (küszöb), egyébként pedig 0-t ( nem aktivált) ad ki.
Nagyszerű. Ez tehát egy neuron aktiválási függvénye. Nincsenek zavarok. Vannak azonban bizonyos hátrányai ennek. Hogy jobban megértsük, gondoljunk a következőkre.
Tegyük fel, hogy létrehozunk egy bináris osztályozót. Valamit, aminek “igent” vagy “nemet” kell mondania ( aktivál vagy nem aktivál ). Egy Step függvény ezt megtehetné neked! Pontosan ezt teszi, mond egy 1-et vagy 0-t. Most gondolj arra a felhasználási esetre, amikor több ilyen neuront szeretnél összekapcsolni, hogy több osztályt hozzon be. Class1, class2, class3 stb. Mi fog történni, ha 1-nél több neuron “aktiválódik”. Minden neuron 1-et fog kiadni ( a lépésfüggvényből). Most hogyan döntenél? Melyik osztályról van szó? Hmm nehéz, bonyolult.
Azt szeretnéd, hogy a hálózat csak 1 neuront aktiváljon, és a többi legyen 0 ( csak akkor mondhatnád, hogy megfelelően osztályozott/azonosította az osztályt ). Á! Ezt így nehezebb betanítani és konvergálni. Jobb lett volna, ha az aktiválás nem bináris lenne, hanem azt mondaná, hogy “50% aktiválva” vagy “20% aktiválva” és így tovább. És akkor ha 1-nél több neuron aktiválódik, akkor meg lehetne találni, hogy melyik neuron a “legmagasabb aktivációjú” és így tovább ( jobb, mint a max, egy softmax, de ezt most hagyjuk ).
Ez esetben is, ha 1-nél több neuron mondja, hogy “100% aktivált”, akkor is fennáll a probléma. tudom! De..mivel vannak köztes aktiválási értékek a kimenethez, a tanulás simább és könnyebb lehet ( kevésbé kacskaringós ) és kisebb az esélye annak, hogy 1-nél több neuron 100%-ban aktiválódik, ha összehasonlítjuk a lépésfüggvénnyel a képzés során ( attól is függ, hogy mit képzelünk el és az adatoktól ).
Oké, tehát szeretnénk, ha valami köztes ( analóg ) aktiválási értékeket adna nekünk ahelyett, hogy azt mondaná, hogy “aktivált” vagy nem ( bináris ).
Az első dolog, ami eszünkbe jut, a Lineáris függvény lenne.
Lineáris függvény
A = cx
Egy egyenes függvény, ahol az aktiválás arányos a bemenettel ( ami a neuronok súlyozott összege ).
Ez így az aktiválások tartományát adja, tehát nem bináris aktiválás. Mindenképpen összekapcsolhatunk néhány neuront, és ha 1-nél több tüzel, akkor vehetjük a max ( vagy softmax) értéket, és ez alapján dönthetünk. Tehát ez is rendben van. Akkor mi a probléma ezzel?
Ha ismered a gradiens ereszkedést a képzéshez, akkor észreveheted, hogy ennél a függvénynél a derivált egy konstans.
A = cx, a derivált x tekintetében c. Ez azt jelenti, hogy a gradiensnek nincs kapcsolata X-szel. Ez egy konstans gradiens, és az ereszkedés konstans gradiensre fog történni. Ha hiba van az előrejelzésben, akkor a visszaterjedés által végrehajtott változások állandóak és nem függnek a bemeneti delta(x) változásától !!!
Ez nem olyan jó! ( nem mindig, de nézzétek el nekem ). Van egy másik probléma is. Gondolj az összekapcsolt rétegekre. Minden réteget egy lineáris függvény aktivál. Ez az aktiválás viszont bemenetként megy a következő rétegbe, és a második réteg súlyozott összeget számol ezen a bemeneten, és ez viszont egy másik lineáris aktiváló függvény alapján tüzel.
Nem számít, hogy hány rétegünk van, ha mindegyik lineáris jellegű, akkor az utolsó réteg végső aktiváló függvénye nem más, mint az első réteg bemenetének csak egy lineáris függvénye! Álljunk meg egy kicsit, és gondolkodjunk el ezen.
Ez azt jelenti, hogy ez a két réteg ( vagy N réteg ) helyettesíthető egyetlen réteggel. Á! Épp most vesztettük el a rétegek egymásra helyezésének képességét ilyen módon. Mindegy, hogyan rakjuk egymásra, az egész hálózat még mindig egyetlen rétegnek felel meg lineáris aktiválással ( lineáris függvények lineáris módon történő kombinációja még mindig egy másik lineáris függvény ).
Lépjünk tovább, jó?
Sigmoid függvény
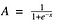
Nos, ez simának és “lépésfüggvényszerűnek” tűnik. Milyen előnyei vannak ennek? Gondolj bele egy pillanatra. Először is, ez nemlineáris jellegű. Ennek a függvénynek a kombinációi is nemlineárisak! Nagyszerű. Most már rétegeket halmozhatunk egymásra. Mi a helyzet a nem bináris aktiválásokkal? Igen, az is! Ez egy analóg aktiválást ad, ellentétben a lépésfüggvénnyel. Sima gradiens is van.
És ha észreveszed, az X értékek között -2 és 2 között az Y értékek nagyon meredekek. Ami azt jelenti, hogy az X értékek bármilyen kis változása ebben a régióban az Y értékek jelentős változását fogja okozni. Á, ez azt jelenti, hogy ez a függvény hajlamos arra, hogy az Y értékeket a görbe bármelyik végére vigye.
A tulajdonságát tekintve jó osztályozónak tűnik? Igen! Valóban az. Hajlamos arra, hogy az aktiválásokat a görbe mindkét oldalára hozza ( x = 2 felett és x = -2 alatt például). Világos megkülönböztetést tesz az előrejelzésen.
Egy másik előnye ennek az aktiválási függvénynek, hogy a lineáris függvénytől eltérően az aktiválási függvény kimenete mindig a (0,1) tartományban lesz, szemben a lineáris függvény (-inf, inf) tartományával. Így az aktivációinkat egy tartományba korlátozzuk. Szép, akkor nem fogja felrobbantani az aktivációkat.
Ez nagyszerű. A szimmoid függvények ma az egyik legszélesebb körben használt aktiválási függvények. Akkor mik a problémák ezzel?
Ha észreveszed, a szigmoid függvény mindkét vége felé az Y értékek hajlamosak nagyon kevésbé reagálni az X változásaira. Mit jelent ez? A gradiens abban a régióban kicsi lesz. Ez a “eltűnő gradiens” problémáját veti fel. Hmm. Tehát mi történik, amikor az aktivációk elérik a görbe mindkét oldalán a “közel vízszintes” rész közelébe?
A gradiens kicsi vagy eltűnt ( nem tud jelentős változást tenni a rendkívül kis érték miatt ). A hálózat nem hajlandó tovább tanulni, vagy drasztikusan lassú ( a felhasználási esettől függően és addig, amíg a gradiens /számítás el nem éri a lebegőpontos értékhatárokat ). Vannak módszerek ennek a problémának a kiküszöbölésére, és a szigmoid még mindig nagyon népszerű az osztályozási problémákban.
Tanh függvény
Egy másik aktiválási függvény, amelyet használnak, a tanh függvény.
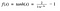
Hm. Ez nagyon hasonlít a sigmoidra. Valójában ez egy skálázott szigmoid függvény!

Oké, most már ez is a fentebb tárgyalt szigmoidhoz hasonló tulajdonságokkal rendelkezik. Nemlineáris természetű, tehát nagyszerű, hogy rétegeket tudunk halmozni! A (-1, 1) tartományhoz van kötve, így nem kell aggódnunk az aktiválások felrobbanása miatt. Egy dolog, amit meg kell említeni, hogy a gradiens erősebb a tanh esetében, mint a sigmoidnál ( a deriváltak meredekebbek). A szigmoid vagy a tanh közötti döntés a gradiens erősségére vonatkozó követelményektől függ. A sigmoidhoz hasonlóan a tanh is rendelkezik az eltűnő gradiens problémával.
A tanh is egy nagyon népszerű és széles körben használt aktiválási függvény.
ReLu
Később jön a ReLu függvény,
A(x) = max(0,x)
A ReLu függvény a fent látható módon. Akkor ad x kimenetet, ha x pozitív, egyébként pedig 0.
Előre úgy tűnik, mintha a lineáris függvény problémái lennének, hiszen a pozitív tengelyen lineáris. Először is, a ReLu nemlineáris természetű. És a ReLu kombinációi is nem lineárisak! ( Valójában ez egy jó közelítő. Bármilyen függvény közelíthető a ReLu kombinációival). Remek, tehát ez azt jelenti, hogy rétegeket halmozhatunk egymásra. Ez azonban nem kötött. A ReLu tartománya [0, inf). Ez azt jelenti, hogy fel tudja fújni az aktiválást.
Egy másik pont, amit itt szeretnék megvitatni, az aktiválás ritkasága. Képzeljünk el egy nagy neurális hálózatot sok neuronnal. A szigmoid vagy tanh használata azt eredményezi, hogy szinte minden neuron analóg módon tüzel ( emlékszel? ). Ez azt jelenti, hogy szinte az összes aktivációt feldolgozzák a hálózat kimenetének leírásához. Más szóval az aktiváció sűrű. Ez költséges. Ideális esetben azt szeretnénk, ha a hálózatban néhány neuron nem aktiválódna, és ezáltal az aktivációk ritkák és hatékonyak lennének.
AReLu ezt az előnyt biztosítja számunkra. Képzeljünk el egy hálózatot véletlenszerűen inicializált súlyokkal ( vagy normalizált ) és a hálózat majdnem 50%-a 0 aktivációt ad a ReLu jellemzője miatt ( 0 kimenet az x negatív értékeire ). Ez azt jelenti, hogy kevesebb neuron tüzel ( ritka aktiváció ) és a hálózat könnyebb. Woah, szép! Úgy tűnik, hogy a ReLu félelmetes! Igen, az, de semmi sem hibátlan… Még a ReLu sem.
A ReLu vízszintes vonala miatt ( negatív X esetén ) a gradiens 0 felé mehet. A ReLu azon régiójában lévő aktiválások esetén a gradiens 0 lesz, ami miatt a súlyok nem lesznek beállítva a süllyedés során. Ez azt jelenti, hogy azok a neuronok, amelyek ebbe az állapotba kerülnek, nem fognak reagálni a hiba/ bemenet változásaira ( egyszerűen azért, mert a gradiens 0, semmi sem változik ). Ezt nevezzük haldokló ReLu problémának. Ez a probléma azt okozhatja, hogy több neuron egyszerűen meghal és nem reagál, így a hálózat jelentős része passzívvá válik. Vannak változatok a ReLu-ban, hogy enyhítsék ezt a problémát azáltal, hogy egyszerűen a vízszintes vonalat nem vízszintes komponenssé teszik . például y = 0.01x x<0 esetén egy enyhén ferde vonal lesz, nem pedig vízszintes vonal. Ez a szivárgó ReLu. Vannak más variációk is. A fő ötlet az, hogy a gradiens ne legyen nulla, és a képzés során végül helyreálljon.
A ReLu kevésbé számításigényes, mint a tanh és a szigmoid, mert egyszerűbb matematikai műveleteket tartalmaz. Ezt érdemes figyelembe venni, amikor mély neurális hálókat tervezünk.
Oké, most melyiket használjuk?
Most, melyik aktiválási függvényt használjuk. Ez azt jelenti, hogy mindenhez csak a ReLu-t használjuk? Vagy a sigmoidot vagy a tanh-t? Nos, igen és nem. Ha tudjuk, hogy a közelíteni kívánt függvénynek vannak bizonyos tulajdonságai, akkor olyan aktiválási függvényt választhatunk, amely gyorsabban közelíti a függvényt, ami gyorsabb képzési folyamathoz vezet. Például a szigmoid jól működik egy osztályozóhoz ( lásd a szigmoid grafikonját, nem mutatja az ideális osztályozó tulajdonságait? ), mert egy osztályozó függvényt a szigmoid kombinációjaként közelíteni könnyebb, mint például talán a ReLu-t. Ami gyorsabb képzési folyamathoz és konvergenciához vezet. Használhatod a saját egyéni függvényeidet is!!!. Ha nem tudod a megtanulni kívánt függvény természetét, akkor talán azt javasolnám, hogy kezdd a ReLu-val, majd dolgozz visszafelé. A ReLu legtöbbször általános közelítőként működik!
Ebben a cikkben megpróbáltam leírni néhány általánosan használt aktiválási függvényt. Vannak más aktiválási függvények is, de az általános gondolat ugyanaz marad. A jobb aktiválási függvények kutatása még folyamatban van. Remélem, megértetted az aktiválási függvény mögötti elképzelést, hogy miért használjuk őket, és hogyan döntjük el, hogy melyiket használjuk.