A Lotka-Volterra egyenletek egy ökológiai ragadozó-zsákmány (vagy parazita-gazda) modellt írnak le, amely feltételezi, hogy, rögzített pozitív konstansok 
(a zsákmány növekedési üteme), 
(a ragadozók zsákmány elpusztításának üteme), 
(a ragadozók halálozási üteme) és 
(a ragadozók zsákmány elfogyasztásával történő növekedésének üteme) esetén a következő feltételek érvényesülnek.
1. Egy 
zsákmánypopuláció 
sebességgel növekszik (arányos a zsákmányok számával), de ezzel egyidejűleg a ragadozók 
sebességgel pusztítják el (arányos a zsákmányok és a ragadozók számának szorzatával).
2. A ragadozók 
populációja 
sebességgel csökken (a ragadozók számával arányosan), de 
sebességgel növekszik (szintén a zsákmány és a ragadozók számának szorzatával arányosan).
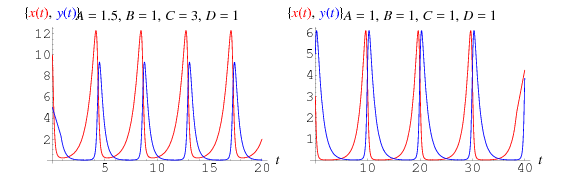
Ez adja a kapcsolt differenciálegyenleteket
 |
 |
 |
(1)
|
 |
 |
 |
(2)
|
megoldásai fentebb ábrázolva, ahol a zsákmányt piros, a ragadozókat kék színnel ábrázoljuk. Egy ilyen modellben a zsákmánygörbe mindig megelőzi a ragadozók görbéjét.
Kritikus pontok akkor fordulnak elő, amikor 
, így
 |
 |
 |
(3)
|
 |
 |
 |
(4)
|
Az egyetlen álló pont tehát a 
pontban található.