Mi a különbség a konkáv és a konvex között?
Ha a lehető legáltalánosabban kellene leírnunk a konkáv és a konvex közötti különbséget, akkor azt mondanánk, hogy minden üreges, tálszerű tárgy konkáv, míg minden olyan tárgy, amely egy rögbilabdára vagy labdára hasonlít, domború alakú. De talán azért használják a konvexet és a konkávot olyan gyakran helytelenül, mert a két szó nem olyan egyszerű, mint amilyennek szeretnénk.
A legtöbb nyelvtani forrás ragaszkodik ahhoz, hogy a mnemotechnika használatával a konvex és a konkáv megfejtése a szóbarlangon keresztül lehetséges. Míg az a fogalom, hogy a konkávot valaminek a “bebarlangolásának” eseményéhez társítjuk, segít a felszíni tulajdonságok megismerésében, addig a grafikonokkal kapcsolatos témák felé ezt a gondolatot zavaró kapcsolatba hozni.
Hogy megértsük, miben különbözik a konkáv és a konvex egymástól, meg kell tanulnunk, hogyan használják az egyes kifejezéseket a matematika, a tükrök, a lencsék, és végül a kreatív íráson belül. Miután eldöntötted, hogy milyen kontextusban szeretnéd használni az olyan szavakat, mint a homorú és a domború, a technikai aspektusaik megismerése lehetővé teszi, hogy magabiztosabban használd őket a mindennapi beszédben.

Mit jelent a konkáv?
A konkávot melléknévként vagy főnévként használják egy tárgy vagy felület olyan alakjának leírására, amely befelé görbült vagy üreges, mint egy tál. Példák a concave szóra egy mondatban:
“She scoopered the ice cream from the container, leaving a concave footprint.”
A The Oxford Dictionary of Word Histories szerint a concave szó a késő középangol nyelvből származik. A konkáv és a homorúság a latin concavus (con- és cavus) kifejezést adja vissza, amely ‘együtt’ és ‘üreges’ jelentéssel fordítható (“Concave”, 110).
Synonyms of concave include:
Dented, depressed, dished, hollow, indented, recessed, and sunken.
Antonyms of concave include:
Domború, domború, kiálló, kiálló, kiugró, kiemelkedő.
Mit jelent a domború?
A domború vagy domborúság szó olyan tárgyat vagy felületet leíró melléknév, amely lekerekített vagy ívelt. Tárgyak tekintetében egy domború tárgy középső felülete szélesebb, mint a külső sarka. Példák a konvexre egy mondatban:
“Beleestem mérges szömörcébe, és most vörös, konvex dudorok vannak az egész bőrömön”.
Synonyms of convex include:
Az ívelt, hajlított, domború, domborodó.
A konvex szavak antonimái többek között:
nyomott, süllyedő.
Konkáv vs. konvex függvények
A konvex függvény olyan folytonos egyenest ábrázol egy grafikonon, ahol egy tartomány középpontja, vagy medián egész értéke nem haladja meg az intervallum átlagát. A homorú függvény a konvex függvény pontos ellentéte, mert ahhoz, hogy f(x) homorú legyen, f(x)-nek negatívnak kell lennie. Hogy a különbségek világosabbá váljanak, íme egy gyors áttekintés a kifejezések összehasonlításáról:
Konkáv felfelé = konvex = konvex lefelé
Konkáv lefelé = konkáv = konvex felfelé
A konkáv és konvex függvények közötti különbség még világosabban megmutatkozik, ha egy grafikonra nézünk. Figyeljük meg, hogy a konvex függvény felfelé nyílik, míg a konkáv függvény lefelé.
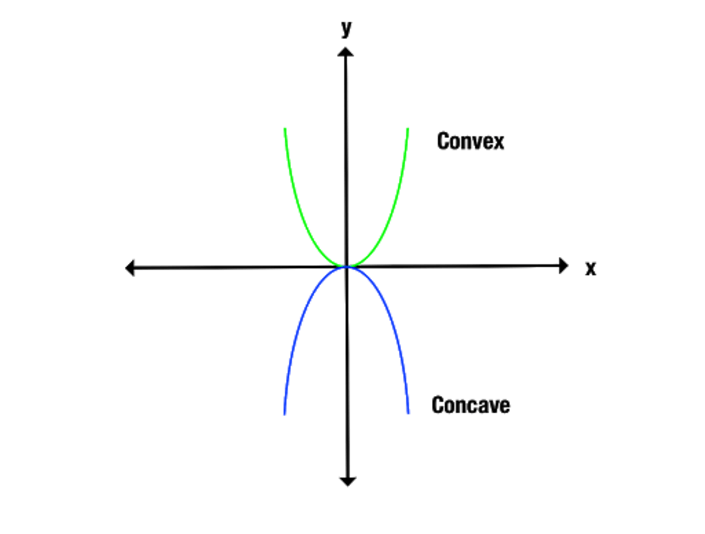
A homorú és konvex függvények azonosításának másik módja, ha a grafikon pontjait összekötjük az x tengely mentén. Egy konkáv függvény csak a grafikon alatti vonalakat köti össze, míg egy konvex függvény csak a grafikon feletti vonalakat.
Kiegészítésképpen a számtan segítségével megfejthetjük, hogy egy függvény konvex vagy konkáv-e vagy sem. Ha f(x) második deriváltja nagyobb, mint nulla, akkor a függvény konvex. Ha viszont f(x) második deriváltja kisebb nulla értéknél, akkor a függvény homorú.
Konvex vs. konkáv sokszögek
Ne essünk pánikba, de a konvex és konkáv szavakat a geometriában is használják. A konvex és konkáv alakzatokról leggyakrabban a sokszögekkel kapcsolatban beszélünk, amelyek olyan alakzatok, amelyeknek legalább három oldala és szöge van.
Reguláris sokszögek léteznek egyenlő oldalakkal és szögekkel, de a konvex és konkáv sokszögek kicsit bonyolultabbak. A konvex sokszögek 180 foknál kisebb belső szögeket tartalmaznak, míg a konkáv sokszögek egy vagy több 180 foknál nagyobb belső szöget tartalmaznak.
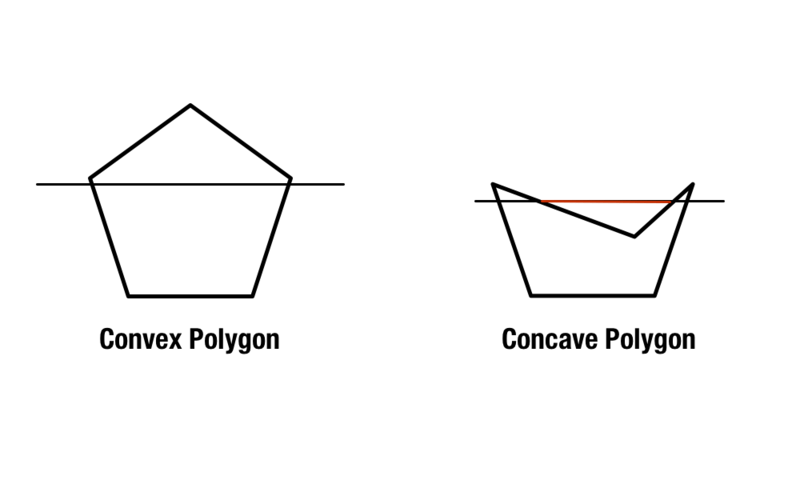
A homorú és konvex sokszögek azonosításának második módszere az, hogy az alakzat sarkaiból kiindulva két átlós vonalat húzunk az alakzaton keresztül. Ha minden vonal az alakzaton belül van, akkor az alakzat konvex. Ha legalább egy vonal az alakzaton kívül keresztezi azt, akkor az alakzat homorú.
Homorú vs. domború tükrök
A homorú és domború szavakat gyakran használják az optikai tárgyak, például tükrök és lencsék tárgyalásakor. Minden domború felület kifelé nyúlik, hasonlóan egy buborékhoz, ami a szélesség hatását kelti. A domború tükrök általában parkolóházakban találhatók, ahol a járművezetőknek széles rálátásra van szükségük a kanyarokban vagy a potenciális holtterekben.

A homorú tükör ezzel szemben befelé görbül, és felfelé fordított, nagyított tükröződést eredményez. Amint azt a Dél-walesi Egyetem Fizikai Kara kimutatta, bárki, akinek van egy fényes kanálja, tesztelheti ezt a megfigyelést, ha megnézi a kanálban lévő tükörképét. A kanál homorú felületén, ahol felveszed az ételt, a tükörképed keskenyen torzul, és fejjel lefelé fogsz látszani. Ha azonban megfordítod a kanalat a domború oldalára, a tükörképed egyenes és kisebb lesz.
A tükröződések azért változnak ilyen nagymértékben a domború és a homorú felületek között, mert akár kifelé, akár befelé görbül a felület, maga a tükör egy gömb része. Mivel egy gömb felülete nem sík, a felületéről visszaverődő fény különböző távolságokat tesz meg, mielőtt a tükörrel érintkezik.
Attól függően, hogy a fény a felület melyik területével érintkezik, a fénysugár visszaverődhet a közeli felületekről, és így egy fókuszáltabb látható területet hoz létre. Ezért van az, hogy ha egy kanál belső felületét nézzük, lehet, hogy csak annak a visszaverődését látjuk, ami a kanál felületéhez legközelebb van – még akkor is, ha az még mindig kisebbnek tűnik. Ráadásul, ha a kanál belsejébe helyeznénk az ujjunkat, a tükör felülete egyszerre két vagy három különböző tükröződést is produkálhat.
Homorú lencse vs. domború lencse
Homorú és domború lencsék léteznek olyan mindennapi tárgyakban, mint a szemüvegek, kontaktlencsék, távcsövek és távcsövek. Hasonlóan a domború és homorú tükrökön történő fényvisszaverődés tudományához, arra is vannak minták, hogy a fény hogyan halad át a homorú és a domború lencséken, hogy látható képet hozzon létre.

Konvex lencsék
A Manocha Akadémia szerint a konvex lencséket konvergens lencséknek nevezik, mivel képesek kicsinyített, nagyított vagy befelé fordított képet létrehozni. Az, hogy mennyire pontosan jelenik meg egy kép a konvex lencsén keresztül, attól függ, hogy a tárgy milyen közel van a lencse fókuszpontjához. Minden domború lencse esetében a lencse mindkét oldalán szimmetrikus fókuszpontok vannak.
Azt, hogy egy tárgy mennyire pontosan jelenik meg egy konvex lencsén keresztül, három alapelv alapján lehet megjósolni:
1. alapelv: A konvex lencsén áthaladó minden fénysugár párhuzamos a főtengellyel, amely a gömblencse abszolút középpontján áthaladó középvonal. Amint a fény a lencsével érintkezik, a fény megtörik, és a másik oldalon a fókuszponton keresztülhalad. A főtengellyel párhuzamos áthaladó fénysugarak a lencse előtt lévő tárgy felett haladnak.
2. alapelv: Minden fénysugár, amely áthalad egy konvex lencse középpontján, egyenes vonalban folytatódik a másik oldalon.
3. alapelv: Bármely fénysugár, amely áthaladt egy fókuszponton, amely ugyanazon az oldalon van, mint a tárgy, a lencsével érintkezve megtörik, és a másik oldalon a főtengellyel párhuzamos lesz.
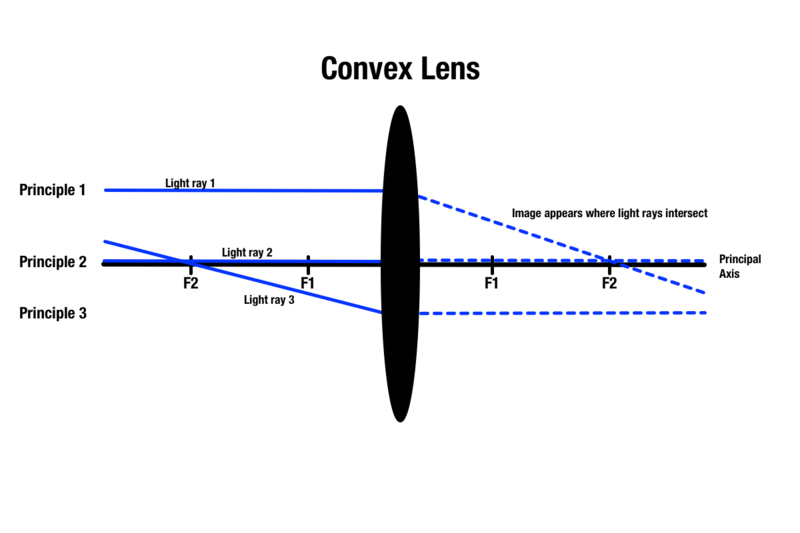
Míg a konvex lencsén keresztül történő képminőség előrejelzésére három alapelv van, a sugárdiagram rajzolásakor csak két alapelvet lehet alkalmazni egy tárgyra. Bármelyik két elv a lencse túloldalán egy fénymetszetet eredményez, amely jelzi azt a területet, ahol a tárgy képe megjelenik.
Minél távolabb van egy tárgy a konvex lencsétől, annál kisebb lesz a kép a túloldalon, és minél közelebb van egy tárgy a konvex lencséhez, annál nagyobbnak fog megjelenni. A legközelebbi fókuszponton túl elhelyezkedő tárgy a tárgy mögött nagyobb képet eredményez. Mint a Manocha Akadémia rámutat, ezt a fajta lencsenagyítást optikai eszközöknél, például nagyítóüvegeknél használják.
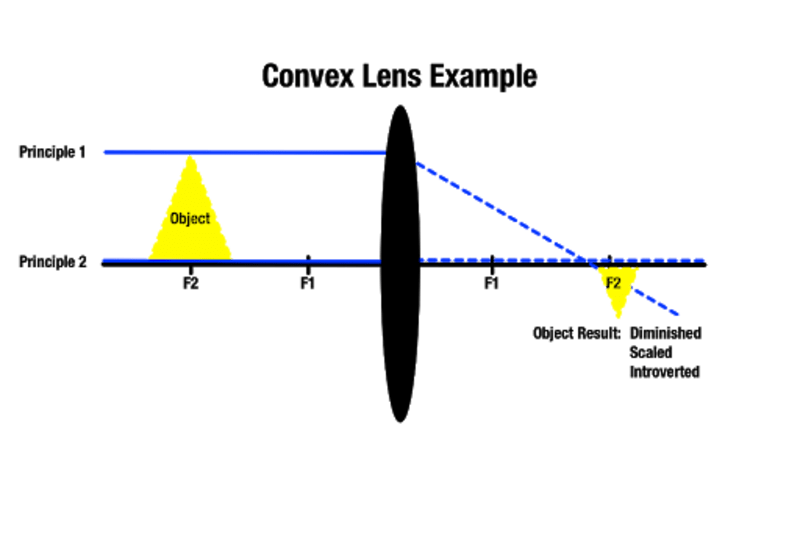
Attól függően, hogy egy tárgy melyik fókuszpontban helyezkedik el, közelítő méretű képet lehet előállítani. Lehetőség van olyan valódi képek létrehozására is, amelyek nem láthatóak, ha az áthaladó fénysugarak soha nem metszik egymást, mert a másik oldalon párhuzamosak. Ebben az esetben az előállított kép végtelen távolságban létezik.
Homorú lencsék
Minden homorú lencsének vastagabb lesz az átmérője, és vékonyabb a közepe, mivel a homorú lencse befelé görbül. A homorú lencsék alakja lehetővé teszi, hogy a fény szétterüljön, amint érintkezik a lencsével, így a virtuális tárgyak kisebbnek tűnnek. A homorú lencse fényszóró képessége ideális lencsévé teszi az olyan eszközökhöz, mint például a zseblámpák, ahol egy központi fényforrás nagyobb felületen használható.
A homorú lencsék három, a domború lencsékhez hasonló elv alapján állítanak elő képeket:
1. alapelv: Bármely, a tárgy felett haladó, a főtengellyel párhuzamos fénysugár a lencsével érintkezve megtörik, és úgy tűnik, mintha a legközelebbi fókuszpont irányából érkezne.
2. alapelv: A homorú lencse középpontján áthaladó bármely fénysugár törés nélkül áthalad.
3. alapelv: Bármely fénysugár, amely a homorú lencse másik oldalán lévő fókuszpont felé irányul, megtörik, és a főtengellyel párhuzamos lesz.
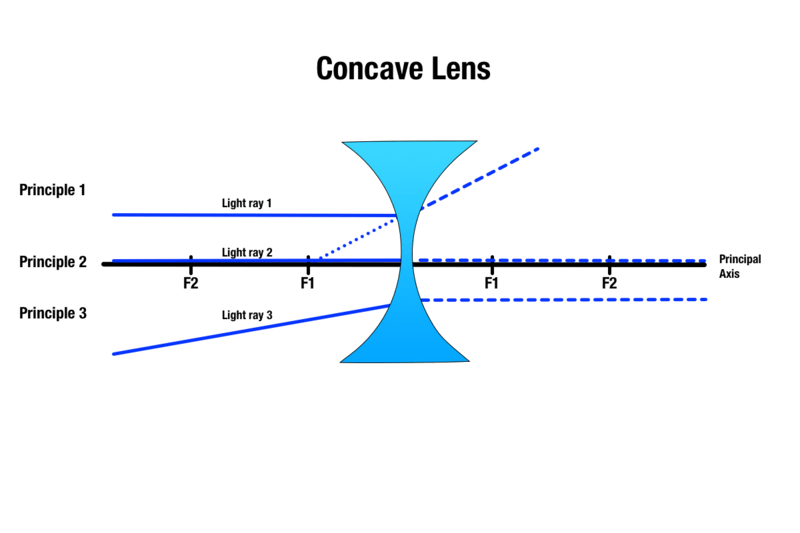
Míg a tárgy képének mérete a tárgynak a homorú lencsétől való távolságától függően változik, a keletkező kép mindig virtuális, függőleges, kisebb, és a lencse ugyanazon oldalán jelenik meg, mint a tárgy.
Konkáv vs. konvex az írásban
A konkáv és a konvex szavak egymással szemben állnak, és lényegében a tárgyak vagy felületek alakját írják le, ugyanúgy, ahogyan az olyan szavakat állítjuk szembe egymással:
- Kicsi vs. kicsi. big
- Tall vs. short
- Slim vs. wide
- Round vs. flat
Mivel a konkáv és a konvex szakszavak, a prózában való leíró használatuk az alkalmi közönség számára metaforikusabb vagy elvont értelmezést eredményezhet. Ez azt jelenti, hogy ha az írók úgy döntenek, hogy a konkávot vagy a konvexet a tipikus használatukon kívül használják, az írónak el kell döntenie, hogy mennyire akarja egyértelművé tenni az írását.
Megfontolandó a melléknév
A konkáv vagy konvex irodalmi használatának kiemelkedő példáját David Foster Wallace (vagy röviden DFW) amerikai író írásai jelentik. DFW hírhedt összetett és technikai jellegű írásmódjáról – és igen, többször használt konvex és konkáv főnevek leírására. Wallace a következő példákban használja a konkávot és a konvexet:
“A kézfejem rendben volt, de nem voltam se nagy, se gyors, a mellkasom majdnem homorú volt, a csuklóm pedig olyan vékony, hogy a hüvelyk- és kisujjammal tudtam volna karkötőzni…”.
– “Tenisz, trigonometria, Tornádó: A Midwestern Boyhood,” Harper’s Magazine.
“…babaszemek, amelyek egy szívzsinór húzásával nyílnak, homorúak, ahol én domború vagyok.”
– “Rend és áramlás Northamptonban”, Conjunctions.
A DFW példák használatának lényege nem pusztán az, hogy megmutassuk, hogyan használták az írók a konvexet vagy a konkávot matematikai kontextuson kívül, hanem inkább az, hogy az írók mérlegeljék, hogy a technikai vagy elvont kifejezések használata hasznos-e a közönségükkel való világos kommunikáció szempontjából.
Az első DFW példában a konkáv használatának azért van értelme, mert valaminek a szerkezetét írja le. De a konkáv és a konvex használata nem tárgyi főnevek, például érzések vagy gondolatok leírására hajlamos elhomályosítani annak jelentését, amit meg akarunk magyarázni. A második DFW példa a konvex és konkáv használata során egy vékony határvonalon mozog, mivel használatuk egyszerre szó szerinti és metaforikus.
FAQ:
Mi a függvény?
A függvény egy egyenes egyenlete egy grafikonon. A függvények a grafikon minden egyes egyenesén más és más, de általános formájuk a következő,
f(x) = x + 1
Minden egyenesfüggvény esetében a függő változó jellemzően f(x), míg a függvényen belüli bármely ismeretlen változót független változónak nevezzük.
Mi a tartomány?
A tartomány a független változók halmaza a grafikonon, amely egy egyenes függvényének felel meg. A tartományokat azért fontos megérteni, mert konkrét pontokat helyeznek el a grafikonon, amelyek megfelelnek egy egyenlet bármely valós kimenetének.
Mi a tartomány?
Minden függvény tartománya egy grafikonon az x- vagy y-tengely mentén minden olyan lehetséges értéket jelöl, amely érvényes értéket ad a függő változónak. Az összes minimális és maximális egész értéket az x- vagy y-tengelyt helyettesítő változókkal azonosítjuk.
Mi az intervallum?
Az intervallum olyan számok halmaza, amelyek egy egyenes egész számait, más néven a tartományt képviselik. Egy zárt intervallum magában foglalja az egyenes két véges pontját, ahol az egyenes már nem létezik egy egész szám tartományán kívül. A nyitott intervallum olyan egész számok halmaza, amelyek nem képviselik a vonal tartományának abszolút végét.
Teszteld magad!
Teszteld, mennyire érted a konvex és a konkáv közötti különbséget a következő feleletválasztós kérdésekkel:
- Miközben egy fényes kanalat nézel, észreveszed, hogy a tükörképed fejjel lefelé áll. A kanál felülete egy _________ felület.
a. Domború
b. Tükör
c. Homorú
d. Fém - A grafikus függvények szempontjából a konvex függvényt néha konvexnek nevezik:
a. Konkáv felfelé
b. Konvex lefelé
c. Konkáv lefelé
d. A és B - Az alábbiak közül melyik nem írja le a homorú felületet:
a. Üreges félgömb
b. Szemlencse
c. Gabonatál
d. Félgömb - Az alábbiak közül melyik nem ír le konvex felületet:
a. Stewie karaktere a Family Guy-ból
b. Gömb
c. Parkolóházi tükör
d. Labdarúgás - Az alábbi alakzatok közül melyik nem létezhet homorú sokszögként:
a. Ötszög
b. Hatszög
c. Háromszög
d. Oktogon
Válaszok
- C: Homorú
- D: A és B
- D: Félgömb
- B: Gömb
- C: Háromszög
Források:
- Bourne, M. “Domain and Range of a Function”. Interaktív matematika, 2019. január 4.
- “Konkáv”. Merriam-Webster szótár, 2019.
- “Konkáv”. The Oxford Dictionary of Word Histories, szerk. Chantrell, 2002, 110. o.
- “Concave and Convex Mirrors”. Manócska Akadémia, YouTube, 2019.
- “Konkáv lencse: Definition & Uses.” Study.com, 2019.
- “Konvex”. Merriam-Webster szótár, 2019.
- “Konvex és homorú lencsék”. Manocha Akadémia, YouTube, 2019.
- “Matematika / Poligonok megértése”. Learnhive Inc. 2018.
- “Reflection from a concave mirror”. UNSW Physics, YouTube, 2017.
- Wallace, D.F. “Tenisz, trigonometria, tornádók: A Midwestern Boyhood.” Harper’s Magazine, 1991.
- Wallace, D.F. “Rend és áramlás Northamptonban”. Conjunctions, 1991.
- Weisstein, Eric W. “Concave Function”. MathWorld-A Wolfram Web Resource, n.d.
- Weisstein, Eric W. “Konvex függvény”. MathWorld-A Wolfram Web Resource, n.d.
A Word Counter egy dinamikus online eszköz, amelyet szavak, karakterek, mondatok, bekezdések és oldalak valós idejű számlálására, valamint helyesírás- és nyelvtani ellenőrzésére használnak.