Introductory Business Statistics

Vizsgáljuk meg a következő adathalmazt.
4; 5; 6; 6; 6; 6; 7; 7; 7; 7; 7; 7; 7; 7; 8; 8; 8; 8; 9; 10

Ezt az adathalmazt a következő hisztogrammal lehet ábrázolni. Minden intervallum szélessége egy, és minden érték az intervallum közepén helyezkedik el.

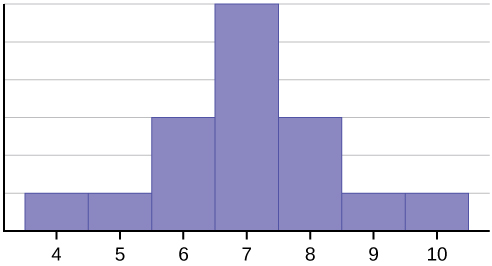
A hisztogram az adatok szimmetrikus eloszlását mutatja. Egy eloszlás akkor szimmetrikus, ha a hisztogram valamelyik pontján egy függőleges vonal húzható úgy, hogy a függőleges vonaltól balra és jobbra lévő alakzat egymás tükörképei legyenek. Az átlag, a medián és a módusz ezeknél az adatoknál egyenként hét. Tökéletesen szimmetrikus eloszlásban az átlag és a medián megegyezik. Ebben a példában egy módusz van (unimodális), és a módusz megegyezik az átlaggal és a mediánnal. Egy olyan szimmetrikus eloszlásban, amelynek két módusza van (bimodális), a két módus eltérne az átlagtól és a mediántól.

Az adatok hisztogramja: 456667777778 nem szimmetrikus. A jobb oldal “levágottnak” tűnik a bal oldalhoz képest. Az ilyen típusú eloszlást balra ferde eloszlásnak nevezzük, mert balra húzódik. Formálisan mérhetjük egy eloszlás ferdeségét, ahogyan matematikailag mérhetjük az adatok középponti súlyát vagy általános “speadness”-ét is. A ferdeség matematikai képlete a következő: . Minél nagyobb a nullától való eltérés, annál nagyobb fokú ferdeséget jelez. Ha a ferdeség negatív, akkor az eloszlás balra ferde, mint az (ábra). A ferdeség pozitív mértéke jobbra ferdeséget jelez, mint például (ábra).

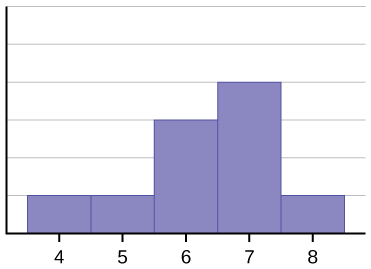
Az átlag 6,3, a medián 6,5, a módusz pedig hét. Vegyük észre, hogy az átlag kisebb, mint a medián, és mindkettő kisebb, mint a módusz. Az átlag és a medián is tükrözi a ferdeséget, de az átlag jobban tükrözi azt.

Az adatok hisztogramja: 67777888910, szintén nem szimmetrikus. Jobbra ferde.

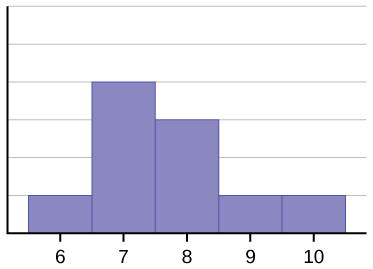
A középérték 7,7, a medián 7,5, a módusz pedig hét. A három statisztika közül az átlag a legnagyobb, míg a módusz a legkisebb. Ismét az átlag tükrözi leginkább a ferdeséget.

Összefoglalva, általában, ha az adatok eloszlása balra ferde, az átlag kisebb, mint a medián, amely gyakran kisebb, mint a módusz. Ha az adatok eloszlása jobbra ferde, a módusz gyakran kisebb, mint a medián, amely kisebb, mint az átlag.

Az átlag, a medián és a módusz, valamint – amint azt rövidesen látni fogjuk – a variancia esetében is léteznek olyan matematikai képletek, amelyek pontos mérőszámokat adnak az adatok eloszlásának ezen jellemzőire. Ha ismét megnézzük a ferdeség képletét, láthatjuk, hogy ez az adatok átlaga és az egyes megfigyelések kockára vetett értéke közötti kapcsolat.

ahol az adatok mintavételi szórása, , és a számtani átlag, pedig a minta mérete.

A számtani átlagot formálisan az eloszlás első momentumának nevezzük. A második momentum, amit látni fogunk, a variancia, a ferdeség pedig a harmadik momentum. A variancia az adatoknak az átlagtól való négyzetes eltéréseit, a ferdeség pedig az adatoknak az átlagtól való kockás eltéréseit méri. Míg a variancia soha nem lehet negatív szám, a ferdeség mértéke lehet, és így határozzuk meg, hogy az adatok jobbra vagy balra ferdék. Normális eloszlás esetén a ferdeség értéke nulla, és minden szimmetrikus adat ferdeségének nulla közelében kell lennie. A ferdeség negatív értékei balra ferde adatokat, a pozitív értékek pedig jobbra ferde adatokat jeleznek. A balra ferde alatt azt értjük, hogy a bal farok hosszú a jobb farokhoz képest. Hasonlóképpen, a jobbra ferde azt jelenti, hogy a jobb farok hosszú a bal farokhoz képest. A ferdeség az eloszlás átlaga körüli aszimmetria mértékét jellemzi. Míg az átlag és a szórás dimenziós mennyiségek (ezért vesszük a variancia négyzetgyökét ), vagyis ugyanazokkal a mértékegységekkel rendelkeznek, mint a mért mennyiségek , addig a ferdeséget konvencionálisan úgy definiálják, hogy az nem dimenziós. Ez egy tiszta szám, amely csak az eloszlás alakját jellemzi. A ferdeség pozitív értéke olyan eloszlást jelöl, amelynek aszimmetrikus farka a pozitívabb X felé nyúlik ki, a negatív érték pedig olyan eloszlást, amelynek farka a negatívabb X felé nyúlik ki. A ferdeség nulla mértéke szimmetrikus eloszlást jelöl.

A ferdeség és a szimmetria fontos lesz, amikor a valószínűségi eloszlásokat tárgyaljuk a későbbi fejezetekben.